This blog is the learning notes for preparing the preliminary exams of Queue theory, referring to Simulation modeling and analysis

Law, A. M., Kelton, W. D., & Kelton, W. D. (2014). Simulation modeling and analysis (Vol. 3). New York: Mcgraw-hill.

1 Basic Simulation Modeling

Basic Simulation Modeling

1.1 The Nature of Simulation

Lectures: - Simulation and modeling of natural processes | 自然过程的仿真与建模 | Python | ABM_哔哩哔哩_bilibili

This is a book about techniques for using computers to imitate, or simulate, the operations of various kinds of real-world facilities or processes.

analytic solution: 解析解

Note: 本文文字部分借助 obsidian + Annotator 插件（Annotator 介绍见 obsidian-annotator)，实现 pdf 文档标注及文字时时提取功能，能够将所有标注的文字提取到 markdown 文件中。图片部分借助 Image auto upload plugin 插件（见 Link ）和 PicGo 实现图片自动上传到 GitHub 图床。然后借助 python 实现简单的文本内容提取，就可以得到纯净的笔记内容。具体操作和实现流程，见之前博客Photography-is-simple/的引言部分教程。

完整笔记链接见： Download Now

Application areas for simulation are numerous and diverse Application areas for simulation:

Designing and analyzing manufacturing systems (制造系统的设计与分析)；
Evaluating military weapons systems or their logistics requirements (军用武器系统及其后勤保障的评估)；
Determining hardware requirements or protocols for communications networks (通信网络中硬件需求或协议的确定)；
Determining hardware and software requirements for a computer system (计算机系统软硬件需求的确定)；
Designing and operating transportation systems such as airports, freeways, ports, and subways (运输系统（如机场、高速公路、港口、地铁等）的设计与运营)：
Evaluating designs for service organizations such as call centers, fast-food restaurants, hospitals, and post offices (服务组织（如呼叫中心、快餐店、医院、邮局等）的评估设计)；
Reengineering of business processes (业务流程的重组)；
Analyzing supply chains (供应链分析)；
Determining ordering policies for an inventory system (库存系统订货策略的确定)；
Analyzing mining operations (采矿作业的分析)。

most real-world systems are too complex to allow realistic models to be evaluated analytically, and these models must be studied by means of simulation.

careful simulation study could shed some light on the question

One indication of this is the Winter Simulation Conference, which attracts 600 to 800 people every year.

several impediments to even wider acceptance and usefulness of simulation 缺点： - 用于大规模系统的模型变得非常复杂 - 仿真往往需要耗费大量时间。但随着计算机运行速度的不断加快，费用逐渐降低，逐渐迎难而解。

First, models used to study large-scale systems tend to be very complex

A second problem with simulation of complex systems is that a large amount of computer time is some-times required.

Finally, there appears to be an unfortunate impression that simulation is just an exercise in computer programming, albeit a complicated one

Perspectives on the historical evolution of simulation modeling may be found in Nance and Sargent (2002).

All of the computer code shown in this chapter can be downloaded from www.mhhe.com/law.

1.2 Systems, Models, and Simulation

系统分类： - 离散系统：状态变量在一些离散时间点上瞬时变化的系统； - 连续系统：状态变量随时间变化而变化的系统。

We categorize systems to be of two types, discrete and continuous.

A discrete system is one for which the state variables change instantaneously at separated points in time

A continuous system is one for which the state variables change continuously with respect to time.

Ways to study a system.

Ways to study a system - 用实际系统的实验与用系统模型的实验 (Experiment with the Actual System vs. Experiment with a Model of the System) - 物理模型与数学模型 (Physical Model vs. Mathematical Model). - 解析解与仿真 (Analytical Solution vs. Simulation).

classify simulation models along three different dimensions: Classify simulation models along three different dimensions: - 静态与动态仿真模型 (Static vs. Dynamic Simulation Models) - 确定的与随机的仿真模型 (Deterministic vs. Stochastic Simulation Models) - 连续的与离散仿真模型 (Continuous vs. Discrete Simulation Models).

The disadvantage of simulation: Stochastic simulation models produce output that is itself random, and must therefore be treated as only an estimate of the true characteristics of the model;

1.3 Discrete Event Simulation

Discrete-event simulation concerns the modeling of a system as it evolves over time by a representation in which the state variables change instantaneously at separate points in time.

We call the variable in a simulation model that gives the current value of simulated time the simulation clock 仿真钟：仿真模型中给出仿真时间当前值的这个变量

two principal approaches have been suggested for advancing the simulation clock: next-event time advance and fi xed-increment time advance.0

the following components will be found in most discrete-event simula-tion models 离散事件仿真模型的组件： - 系统秋态：播述在某一特定时刻系统所必需的一组状态变量的集合。 - 伤真钟：给出仿真时间当前值的变量。 - 事件表：包含下一次每类事件发生时间的表。 - 统计计数器：用于存储系统性能统计信息的变量。 - 初始化例程：零时刻对伤真模型进行初始化的子程序。 - 定时例程：用于从事件表中确定下一事件并将伤真钟推进到该下一事件发生时间的一个子程序。 - 事件例程；当某一特定类型事件发生时更新系统状态的子程序（每类事件有一个事作例程）。 - 库例程：根据确定的概率分布产生随机观测值的一组子程序，作为仿真模型的部分。 - 报告生成器：计算性能期望度量的估计值（通过统计计数器），并在仿真结束时生成一个报告的一个子程序。 - 主程序：调用定时例程来确定下一事件，然后将控制转移到相应的事件例程以适当更新系统状态的一个子程序。主程序还可以检查终止条件并在终止时调用报告生成器。

1.4 Simulation of a Single-server Queueing System

To measure the performance of this system, we will look at estimates of three quantities. To measure the performance of the discrete simulation system: - 平均延误时间的期望值：First, we will estimate the expected average delay in queue of the n customers completing their delays during the simulation; we denote this quantity by $d(n)$. - 队列中顾客平均数的期望值： the expected average number of customers in the queue (but not being served), denoted by $q(n)$. - 服务台的期望利用率：The expected utilization of the server is the expected proportion of time during the simulation.

First, we will estimate the expected average delay in queue of the n cus-tomers completing their delays during the simulation; we denote this quantity by d(n).

the expected average number of customers in the queue (but not being served), denoted by q(n),

The expected utilization of the server is the expected pro-portion of time during the simulation [from time 0 to time T(n)]

To recap, the three measures of performance are the average delay in queue dˆ(n), the time-average number of customers in queue qˆ (n), and the proportion of time the server is busy uˆ (n).

1.5 Simulation of An Inventory System

1.6 Parallel/Distributed Simulation and The High Level Architecture

logic is executed in order of the events’ simulated time of occurrence; i.e., the simu-lation is sequential. sequential. a. 串行的

1.7 Steps in a Sound Simulation Study

As one proceeds with the study, it may be necessary to go back to a previous step.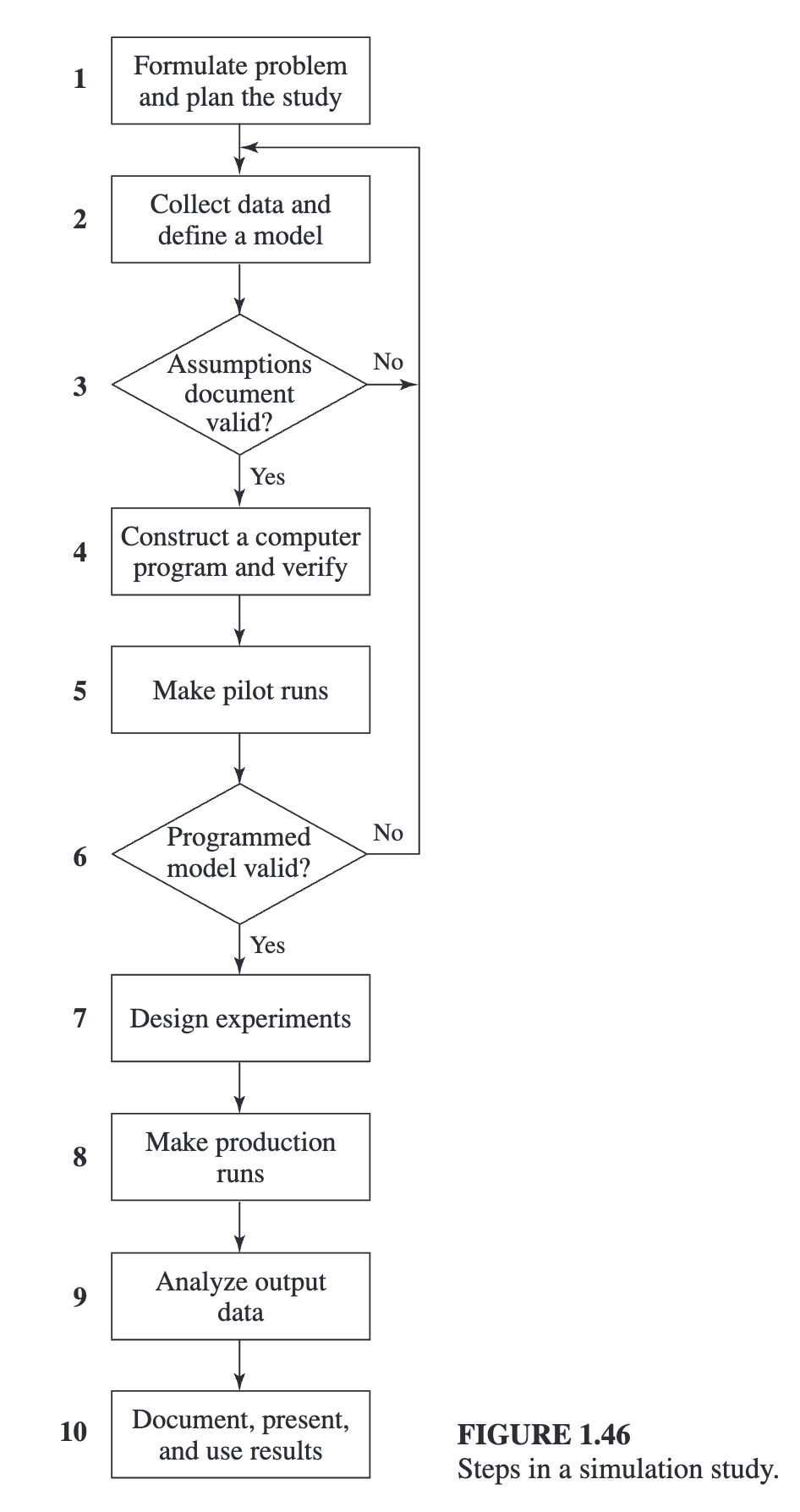

Steps: 1. 问题形式化与制定研究计划 2. 收集数据并定义模型 3. 假设文档是有效的吗 4. 编制计算机程序并校验 5. 进行操控运行 6. 编程模型有效吗 7. 设计实验 8. 进行批次运行 9. 分析输出数据 10. 形成文件，提交及使用结果

1.8 Advantages, Disadvantages and Pitfalls of Simulation

Some possible advantages of simulation that may account for its widespread appeal are the following.

Most complex, real-world systems with stochastic elements cannot be accurately described by a mathematical model that can be evaluated analytically

Simulation is not without its drawbacks. Some disadvantages are as follows

2. Chapter 2 Modeling Complex Systems

Most real-world systems, however, are quite complex, and coding them without supporting software can be a diffi cult and time-consuming task

2.2 List Processing in Simulation

two approaches to storing lists of records in a computer—sequential and linked allocation 存储记录表的两种方式： - 顺序分配 (Sequential allocation) - 链式分配 (Linked allocation)

3. Simulation Software

3.1 Introduction

several features needed in programming most discrete-event simulation models, including: several features needed in programming most discrete-event simulation models, including: •

• - Generating random numbers, that is, observations from a $U(0,1)$ probability distribution (产生随机数，即均匀概率分布 $U(0,1)$ 的观测值)； - Generating random variates from a specified probability distribution (e.g., exponential) (产生一个特定概率分布（例如，指数分布）的随机变量)； - Advancing simulated time (推进仿真时间)； - Determining the next event from the event list and passing control to the appropriate block of code (从事件表中确定下一事件，并将控制权转交给适当的代码块)； - Adding records to, or deleting records from a list (向一个表添加记录或从表中删除记录)； - Collecting output statistics and reporting the results (搜集输出统计信息并生成结果报告)； - Detecting error conditions (探测错误发生的条件)。

Section 3.5 gives brief descriptions of Arena, ExtendSim, and Simio, which are popular general-purpose simulation packages

3.3 Classification of Simulation Software

There are two main types of simulation packages for discrete-event simulation, namely, general-purpose simulation software and application-oriented simulation software.

e used the event-scheduling approach to discrete-event simulation modeling

4. Review of Basic Probability and Statistics

4.1 Introduction

The use of probability and statistics is such an integral part of a simulation study

In this chapter we establish statistical notation used throughout the book and review some basic probability and statistics particularly relevant to simulation.

4.2 Random Variables and Their Properties

Notations: - Sample space $S$: The set of all possible outcomes of an experiment - Random variable: a function (or rule) that assigns a real number (any number greater than $-\infty$ and less than $\infty$ ) to each point in the sample space $S$ > In general, we denote random variables by capital letters such as $X, Y, Z$ and the values that random variables take on by lowercase letters such as $x, y, z$.

Distribution function (sometimes called the cumulative distribution function) $F(x)$.
Joint probability mass function $p(x, y)$
Joint probability density function $(f(x, y)$
(Marginal) Probability density function $f_X (x)$
Mean or Expected value of $X_i$ is $\mu_i$ or $\mathbb{E}(X_i)$
Variance $\sigma_i^2$ or $\text{Var}(X_i)$

A distribution function F(x) has the following properties Properties: - $0 \leq F(x) \leq 1, \forall x$ - If $x_1 < x_2$, then $F(x_1) \leq F(x_2)$ - $\lim_{x\to \infty} F(x) = 1$ and $\lim_{x\to 0} F(x) = 0$

p(x, y) is called the joint probability mass function

joint probability density function

(marginal) probability density functions of X and Y \[ \begin{align*} f_X (x) = \int_{-\infty}^{\infty} f(x, y) \text{ d} y \\ f_Y (y) = \int_{-\infty}^{\infty} f(x, y) \text{ d} x \end{align*} \]

The mean or expected value of the random variable Xi Then the following are important properties of means:
1. $\mathbb{E}(cX) = c \mathbb{E}(X)$. 2. $\mathbb{E}(\sum\limits_{i=1}^n c_i X_i) = \sum\limits_{i=1}^n c_i \mathbb{E} (X_i)$ even if the $X_i$’s are dependent (相关的).

hen the following are important properties of means

The variance of the random variable Xi will be denoted by s2i or Var(Xi)

The variance has the following properties: Properties of variance: - $\text{Var}(X_i) \ge 0$ - $\text{Var}(c X_i) = c^2 \text{Var}(X_i)$ - $\text{Var}(\sum\limits_{i=1}^n X_i) = \sum\limits_{i=1}^n \text{Var}(X_i)$ if the Xi’s are independent (or uncorrelated, as discussed below).

In particular, suppose that Xi has a normal distribution with mean $\mu_i$ and standard deviation $\sigma_i$. In this case, for example, the probability that $X_i$ is between $\mu_i - 1.96\sigma_i$ and $\mu_i + 1.96\sigma_i$ is 0.95.

In particular, suppose that Xi has a normal dis-tribution with mean mi and standard deviation si. In this case, for example, the prob-ability that Xi is between mi 2 1.96si and mi 1 1.96si is 0.95

he covariance between the random variables Xi and Xj (where i 5 1, 2, . . . , n; j 5 1, 2, . . . , n) Covariance: \[ C_{ij} = \mathbb{E}\left[(X_i - \mu_i )(X_j - \mu_j)\right] = \mathbb{E}(X_i X_j) - \mu_i\mu_j \]

Note: covariances are symmetric, that is, $C_{ij} = C_{ji}$, and if $i=j$, then $C_{ij}=C_{ji}=\sigma_i^2$.

If $Cij =0$, the random variables Xi and Xj are said to be uncorrelated.

As a result, we use the correlation rij, defi ned b Correlation $\rho_{ij}$ or $\text{Cor} (X_i, X_j)$: \[ \rho_{ij} = \frac{C_{ij}}{\sqrt{\sigma_i^2 \sigma_j^2}} \]

4.3 Simulation Output Data and Stochastic Process

A stochastic process is a collection of “similar” random variables ordered over time, which are all defi ned on a common sample space. The set of all possible val-ues that these random variables can take on is called the state space Note: 随机过程是按时间排序的“类似的”随机变量的几何，随机变量全部定义在共同样本空间上。这些随机变量可以取的所有可能值的集合称为状态空间。

Example: For a single-server queueing system, e.g., $M / M /1$ queue, with IID inter-arrival times $A_1, A_2, \cdots$, IID service times $S_1, S_2, \cdots$ and customers served in a FIFO manner. 定义在队列中的延误时间 (delays in queue) $D_1, D_2, \cdots$ as follows:

\[ \begin{align} D_1 &= 0 \\ \\ D_{i+1} &= \max\{D_i + S_i - A_{i+1}, 0\} \quad \text{for} i = 1,2,\cdots \end{align} \] Note: $D_i$ and $D_{i+1}$ are positively correlated. - 令 $Q(t)$ 为在 $t$ 时刻在队列中的顾客数，则 $\{Q(t), t \ge 0\}$ 是一个连续时间随机过程，其状态空间为 $\{0, 1,2, \cdots \}$ - 令 $C_i$ 为第 $i$ 个月的总成本（如订货、存储和缺货成本的总和），则 $C_1, C_2, \cdots$ 是一个离散时间随机过程，其状态空间为非负实数。

To draw inferences about an underlying stochastic process from a set of simula-tion output data, one must sometimes make assumptions about the stochastic proces

. A discrete-time stochastic process X1, X2, . . . is said to be covariance-stationary 一个常见的例子是假设随机过程是协方差平稳的。Definition: \[ \begin{align} \mu_i = \mu \quad \text{for } i =1,2,\cdots \text{ and } - \infty < \mu < \infty \\ \\ \sigma_i^2 = \sigma^2 \quad \text{for } i =1,2,\cdots \text{ and } \sigma^2 < \infty \end{align} \] 因此，对于一个协方差平稳过程，均值和方差是不随时间变化而变化的，且两个观测值 $X_i$ 和 $X_{i+j}$ 之间的协方差仅仅取决于间隔 $j$，而不取决于实际时间值 $i$ 和 $i+j$。

For a covariance-stationary process, For a covariance-stationary process, we denote the covariance and correlation between $X_i$ and $X_{i+j}$ by $C_j$ and $\rho_j$, respectively, where \[ \rho_j=\frac{C_{i, i+j}}{\sqrt{\sigma_i^2 \sigma_{i+j}^2}}=\frac{C_j}{\sigma^2}=\frac{C_j}{C_0} \quad \text { for } j=0,1,2, \ldots \]

4.4 Estimation of Means, Variances, and Correlations

our primary objec-tive is to estimate m; For IID random variables - Sample mean \[ \bar{X}(n)=\frac{\sum\limits_{i=1}^nX_i}{n} \] - Sample variance \[ S^2(n) = \frac{\sum\limits_{i=1}^n\left[X_i-\bar{X}(n)\right]^2}{n-1} \]

Variance of sample mean \[ \operatorname{Var}[\bar{X}(n)]= \frac{\sigma^2}{n} \]
Unbiased estimator of $\operatorname{Var}[\bar{X}(n)]$ \[ \widehat{\operatorname{Var}}[\bar{X}(n)]=\frac{S^2(n)}{n}=\frac{\sum_{i=1}^n\left[X_i-\bar{X}(n)\right]^2}{n(n-1)} \]

For covariance-stationary stochastic process - Sample variance

\[ \operatorname{E}[S^2(n)]=\sigma^2 \left[1 - 2\frac{ \sum\limits_{j=1}^{n-1}(1-j / n) \rho_j}{n-1}\right] \]

Variance of the sample mean \[ \operatorname{Var}[\bar{X}(n)]=\sigma^2 \frac{\left[1+2 \sum\limits_{j=1}^{n-1}(1-j / n) \rho_j\right]}{n} \]

covariance-stationary stochastic process

there are two sources of error: the bias in S 2(n) as an estimator of s2 and the negligence of the correlation terms

4.5 Confidence Intervals and Hypothesis Tests for the Mean

standard normal random variable; - Standard normal random variable: \[ \Phi(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^z e^\frac{-y^2 }{2}\operatorname d y \qquad -\infty<z<\infty \]

a particular n, coverage decreases as the skewness of the distribution gets larger - skewness \[ \nu=\frac{E\left[(X-\mu)^3\right]}{\left(\sigma^2\right)^{3 / 2}} \quad-\infty<\nu<\infty \]

5. Building Valid, Credible, and Appropriately Detailed Simulation Models

5.1 Introduction and Definitions

One of the most diffi cult problems facing a simulation analyst is that of trying to determine whether a simulation model is an accurate representation of the actual system being studied, i.e., whether the model is valid

We begin by defining the important terms used in this chapter, including verifica-tion, validation, and credibility. - Verification is concerned with determining whether the “assumptions document” - Validation is the process of determining whether a simulation model is an accurate representation of the system, for the particular objectives of the study. - A simulation model and its results have credibility if the manager and other key project personnel accept them as “correct.”

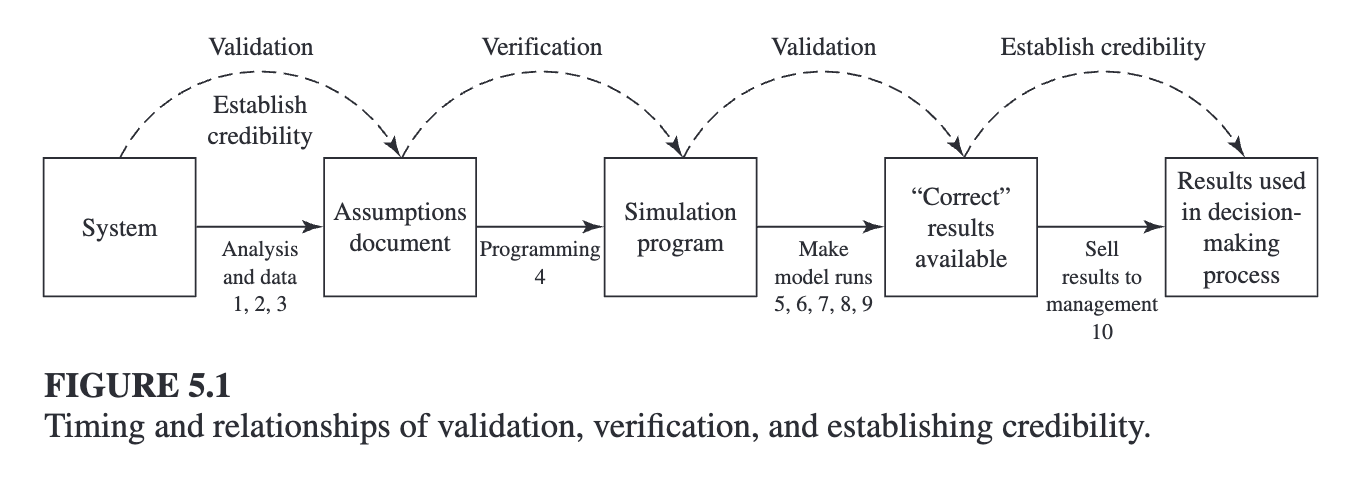
5.2 Guidelines for Determining the Level of Model Detail

We now present some general guidelines for determining the level of detail required by a simulation model 确定仿真模型所需详细程度的某些一般准则： - 认真定义要研究的问题的细节以及将用于评估的性能度量； - 实体通过放着呢模型并不总是必须于是提通过对应系统相同； - 使用主题专家 (SME) 和灵敏度分析来帮助决定模型的详细程度； - 建模初学者常犯的错误是模型的细节过多； - 在模型中不要有比解决关注的问题所必须的更多细节，前提是模型必须足够详细保证其是可信的； - 模型的详细程度应该与可用数据的类型相一致； - 在实际的所有仿真研究中，时间和经费约束是确定模型详细程度的主要因素； - 如果要研究的因素过多，则使用一个“粗”仿真模型或者一个解析模型来识别哪些因素对于系统性能有重大影响。

5.3 Verification of Simulation Computer Programs

In this section we discuss eight techniques that can be used to debug the computer program of a simulation model

5.4 Techniques for Increasing Model Validity and Credibility

Collect High-Quality Information and Data on the System Collect High-Quality Information and Data on the System: - Conversations with subject-matter experts - Observations of the system - Existing theory - Relevant results from similar simulation studies - Experience and intuition of the modelers

Interact with the Manager on a Regular Basis

6. Selecting Input Probability Distributions

6.1 Introductions

To carry out a simulation using random inputs such as interarrival times or demand sizes, we have to specify their probability distributions.

If it is possible to collect data on an input random variable of interest, these data can be used in one of the following approaches to specify a distributio 如果可能收集到相关的输入随机变量数据，这些数据可用于以下的方法之一，以确定一个分布： 1. 在仿真钟直接使用数据值本身。例如，如果用数据代表服务时间，那么仿真中一旦需要服务时间就使用一个数据值。这有时叫做 跟踪驱动仿真 (Trace-driven simulation) 2. 以某种方式使用数据值本身来定义一个经验分布函数 (seeing Sec 6.2)。如果这些数据代表服务时间，当仿真中需要服务时间时，就可以从该分布中取样。 3. 使用统计推理的标准方法对数据 “拟合” 一个理论分布形式，例如指数分布或者泊松分布，并进行假设检验以确定你和的优良度。

Two drawbacks of approach 1 are that the simulation can only reproduce what has happened historically and that there is seldom enough data to make all the de-sired simulation runs.

6.2 Useful Probability Distributions

6.2.1 Parameterization of Continuous Distributions

However, if the parameters are defi ned correctly, they can be classifi ed, on the basis of their physical or geometric interpretation, as being one of three basic types: location, scale, or shape parameters. 可以将参数归类为三种基本类型中的一类： - Location parametere $\gamma$ : 制定了分布取值范围的横坐标 (absciss, $x$ 轴）位置点，通常是分布的范围的中点（如正态分布的均值 $\mu$ ）或者下端点； - Scale parametere $\beta$ : 决定了分布范围取值的测量比例，或单位，标准差 $\sigma$ 是标准正态分布的比例参数； - Shape parameter $\alpha$ : 决定了相关分布一般类型内的基本形状。$\alpha$ 的变化一般会改变分布的性质（如斜歪），较之于位移或者比例参数，其变化是更根本性的。注：有些分布（如 指数分布 或 正态分布 ）没有形状参数，有些分布（如 贝塔分布 ）可以有两个形状参数。

6.2.2 Continuous Distributions

Table 6.3 gives information relevant to simulation modeling applications for 13 con-tinuous distributions. Possible applications are given fi rst to indicate some (certainly not all) uses of the distribution 13 个连续分布 - 均匀分布 Uniform - 指数分布 Exponential - 伽马分布 Gamma - 韦布尔分布 Weibull - 正态分布 Normal - 对数正态分布 Lognormal - 贝塔分布 Beta - 皮尔逊 V 型分布 Pearson type V - 皮尔逊 VI 型分布 Pearson type VI - 对数逻辑斯蒂分布 Log-logistic - 约翰逊 $S_B$ 分布 Johnson $S_B$ - 三角分布 Triangular

6.2.3 Discrete Distribution

The descriptions of the six discrete distributions in Table 6.4 六个离散分布： - 伯努利分布 Bernoulli - 离散均匀分布 Discrete Uniform - 二项分布 Binomial - 几何分布 Geometric - 负二项分布 negative binomial - 泊松分布 Poisson

6.2.4 Empirical Distribution

In some situations we might want to use the observed data themselves to specify directly (in some sense) a distribution, called an empirical distribution 经验分布：使用观测数据本身直接（在某种意义下）定义一个分布，这称为经验分布

For continuous random variables, the type of empirical distribution that can be defi ned depends on whether we have the actual values of the individual original observations X1, X2, . . . , Xn rather than only the number of Xi’s that fall into each of several specifi ed intervals. (The latter case is called grouped data or data in the form of a histogram.) 对于连续随机变量，能定义的经验分布的类型依赖于我们是否具有单个原始观测 $X_1, X_2, \cdots, X_n$ 的实际值，而不是只有 $X_i$ 落到若干规定的区间的个数（后者称为 分组数据 ，或者称为 直方图形式数据 ）

s is also the way we would like a con-tinuous distribution

The random values generated from this distribution, however, will still be bounded both below (by a0) and above (by ak);

6.3 Techniques for Assessing Sample Independence

前文讨论的很多统计方法都有一个重要的假设，那就是观测值 $X_1, X_2, \cdots, X_n$ 是某个基本分布的独立的（或随机的）样本。例如最大似然估计（Seeing sec 6.5）和 $\chi^2$ 检验 (Seeing 6.6.2) 都假设了独立性。

如果关于独立性的假设不成立，那么这些统计方法也许是无效的。

If the assumption of independence is not satisfi ed, then these statistical techniques may not be valid We now describe two graphical techniques for informally assessing whether the data X1, X2, . . . , Xn (listed in time order of collection) are independent. 非正式评估数据 $X_1, X_2, \cdots,$ 是否独立 (independent) 的两种图形方法： - 相关系数图 correlation plot。如果样本相关系数 $\hat \rho_j$ 与 0 有很大的数量差异，那么这是 $X_i$ 非独立的有力证书 - 观测数据 $X_1, X_2, \cdots$ 关于 $(X_i, X_{i+1})$ 点对的散点图 scatter plot。如果 $X_i$ 是独立的，则期望点 $(X_i, X_{i+1})$ 会随机地分布在 $(X_i, X_{i+1})$ 平面的第一象限。如果正相关，则点会呈现一条正斜率的直线；否则呈现 负斜率 的直线。

其他的参数（即对 $X_i$ 的分布不做假设）统计检验方法，可以用于正式地检验 $X_1, X_2, \cdots， X_n$ 是否独立。 - 冯·诺伊曼比率的排序版本 (A a rank version of Von Neumann's ratio)。一个潜在的缺陷就是该检验方法假设数据之间没有“粘性”（即对于 $i\neq j, X_i=X_j$）。对于离散数据来说，这个要求一般是不满足的。

There are also several nonparametric (i.e., no assumptions are made about the distributions of the $X_i$’s) statistical tests that can be used to test formally whether $X_1, X_2, \cdots, X_n$ are independent.

6.4 Activity 1: Hypothesizing Families of Distributions

The fi rst step in selecting a particular input distribution is to decide what general families 选择特定输入分布的第一步就是要决定哪些类常用分布形状上与其相似，而不考虑这些类别的具体参数值。

6.4.1 Summary Statistics

Useful summary statistics

In particular, $cv =1$ for the exponential distribution, regardless of the scale parameter $\beta$

For a discrete distribution, the lexis ratio $\tau$ plays the same role that the coefficient of variation does for a continuous distribution.

The skewness $\nu$ is a measure of the symmetry of a distribution.

6.4.2 Histograms

The quantile summary [see, for example, Tukey (1970)] is a synopsis of the sample that is useful for determining whether the underlying probability density function or probability mass function is symmetric or skewed to the right or to the left

6.5 Activity II: Estimation of Parameters

Estimating the parameters from the data

we must somehow specify the values of their parameters in order to have completely specifi ed distributions for possible use in the simulation

We shall consider explicitly only one type, maximum-likelihood estimators (MLEs), for three reasons: We shall consider explicitly only one type, maximum-likelihood estimators (MLEs), for three reasons:
- MLEs have several desirable properties often not enjoyed by alternative methods of estimation, e.g., least-squares estimators, unbiased estimators, and the method of moments; - The use of MLEs turns out to be important in justifying the chi-square $\chi^2$ goodness-of-fit test (see Sec. 6.6.2); - The central idea of maximum-likelihood estimation has a strong intuitive appeal.

MLEs have several desirable statistical properties, some of which are as follows MLE 具有一些很理想的统计性质，包括： - 对于大多数常用的分布，MLE 是唯一的；也就是说，对于其他任何的 $\theta$ 值，$L(\hat \theta)$ 都严格大于 $L(\theta)$; - 虽然 MLE 不必是无偏的，一般情况下，$\hat \theta$ 的渐进分布 $(n \to +\infty)$ 的均值等于 $\theta$ - MLE 具有不变性（invariant）。如果对于某个函数 $h, \varphi = h(\theta)$, 那么 $\varphi$ 的 MLE 为 $h(\hat \theta)$ （无偏性不是不变性）； - MLE 是渐进正态分布的； - MLE 是强一致性的，即 $\lim\limits_{n \to + \infty} \hat \theta = \theta, w.p. 1$

if the simulation appeared to be sensitive to u, we might seek a better estimate of u; 模型不确定性 和 参数不确定性

When we choose the distributions to use for a simulation model, we generally don’t know with absolute certainty whether these are the correct distributions to use, and this lack of complete knowledge results in what we might call model uncertainty

given that cer-tain input distributions have been selected, we typically do not know with com-plete certainty what parameters to use for these distributions, and we might call this parameter uncertainty.

There have been a number of methods suggested for addressing the problem of input-model uncertainty, including the following [see Barton (2012) and Henderson (2003)] There have been a number of methods suggested for addressing the problem of
input-model uncertainty, including the following [see Barton (2012) and Henderson (2003)]:
- 贝叶斯模型平均值方法 (Bayesian model averaging) [Chick (2001), Zouaoui and Wilson (2003, 2004)]
- Delta 方法 (Delta-method approaches) [Cheng and Holland (1997, 1998, 2004)] - 元模型辅助的自举方法 (Metamodel-assisted bootstrapping) [Barton et al. (2013), Chapter 12]; see Cheng (2006) and Efron and Tibshirani (1993) for a discussion of bootstrap resampling
- 非参数的自举方法 (Nonparametic bootstrapping) [Barton and Schruben (1993, 2001)] - 基于随机效用模型的快速方法 (Quick method based on a random-effects model) [Ankenman and Nelson (2012)]

Unfortunately, most of these methods are reasonably complicated and make assumptions that may not always be satisfi ed in practice

6.6 Activity III: Determining How Representative The Fitted Distributions Are

After determining one or more probability distributions that might fi t our observed data in Activities I and II, we must now closely examine these distributions to see how well they represent the true underlying distribution for our data 评估拟合的分布的质量的方法： - 启发式方法（ Heuristic procedures ） - 拟合优良度假设检验法（ Goodness-of-fit hypothesis tests ）

五个启发式方法： - 密度直方图和频率比较 - 分布函数差图 - 概率图（quantile–quantile ( Q–Q) plot、probability–probability (P–P) plot）

For discrete data, a frequency comparison is a graphical comparison of a histo-gram of the data with the mass function pˆ ( x) of a fi tted distribution

quantile–quantile ( Q–Q) plot

probability–probability (P–P) plot

6.6.2 Goodness-of-Fit Tests

A goodness-of-fit test is a statistical hypothesis test (see [[#4.5 Confidence Intervals and Hypothesis Tests for the Mean|Sec. 4.5]]) that is used to assess formally whether the observations $X_1, X_2, \cdots , X_n$ are an independent sample from a particular distribution with distribution function $\hat F$. 拟合优良度检验可以用于检验下面的原假设：

Note: 未能拒绝 $H_0$ 并不意味着“接受 $H_0$ 为真“

First, failure to reject H0 should not be interpreted as “accepting H0 as being true.” 具体的拟合优良度检验方法： - $\chi^2$ 检验 - 科尔莫戈罗夫-斯米尔洛夫检验 - 安德森-达林检验 - 泊松过程检验

Kolmogorov-Smirnov (K-S) tests for goodness of fi t, on the other hand, compare an empirical distribution function with the distribution function Fˆ of the hypothesized distribution 正如我们刚刚看到的一样，$\chi^2$ 检验可以看做将数据直方图与拟合分布的密度函数或者质量函数进行比较正式的对比。在连续情况下应用 $\chi^2$ 检验的一个实际困难，即如何确定区间。另一方面，拟合优良度的科尔莫戈罗夫-斯米尔洛夫（Kolmogorov-Smirnor, K-S）检验将经验分布函数与假设分布的分布函数 $\hat F$ 作对比。正如我们将要看到的一样，K-S 检验不需要以任何形式对数据分组，因此没有任何信息丢失；这些解决了区间划分这个麻烦问题。K-S检验另一个优点就是，它们对于任意样本大小 $n$（在所有参数都已知的情况下）都是（严格）有效的，而x检验只在渐近意义上有效。最后，在很多可选分布的情况下，K-S检验能力比 $\chi^2$ 检验强；参见，例如，Stephens（1974）。

Nevertheless, K-S tests do have some drawbacks, at least at present. Most seri-ously, their range of applicability is more limited than that for chi-square tests.

6.10 Specifying Multivariate Distributions Correlations, and Stochastic Processes

So far in this chapter we have considered only the specifi cation and estimation of the distribution of a single, univariate random variable at a time 本章目前为止，讨论的知识每次确定和估计单个、单随机变量的分布。如果仿真模型需要的输入只是标量随机变量，而且如果他们在模型之间相互独立，那么对每个输入重复地使用至今讨论的方法就足够了。

There are systems, however, in which the input random variables are statisti-cally related to each other in some way: 然而，有些系统的输入随机变量之间以某种方式统计相关： - 有些输入随机变量共同形成一个随机向量，具有某种多元（或联合）概率分布，需要建模着确定。 Some of the input random variables together form a random vector with some multivariate (or joint) probability distribution (see Sec. 4.2) to be specified by the modeler.

6.10.2 Specifying Arbitrary Marginal Distributions and Correlations

In each of these cases, the fi tted member of the multivariate distribution family involved (normal, lognormal, Johnson, or Bézier) determined the correlation between pairs of the component random variables in the vector, as well as their marginal distributions;

We may want to allow for pos-sible correlation between various pairs of input random variables to our simulation model,

6.10.3 Specifying Stochastic Process

there are situations in which a sequence of input random vari-ables on the same phenomenon are appropriately modeled as being draws from the same (marginal) distribution, yet might exhibit some autocorrelation between themselves within the sequence 平稳随机过程： - AR 和 ARMA 过程 - 伽马过程 - ARTA 过程 - VARTA 过程

Standard autoregressive (AR) or autoregressive moving-average (ARMA) models,

6.11 Selecting a Distribution in the Absence of Data

In some simulation studies it may not be possible to collect data on the random variables of interest, so the techniques of Secs. 6.4 through 6.6 are not applicable to the problem of selecting corresponding probability distributions.

6.12 Models of Arrival Processes

We call the stochastic process {N(t), t $ 0} an arrival process since, - Arrival process

6.12.1 Poisson Processes

defi ne a Poisson process, state some of its important properties Definition: - 顾客每次到达一个； - $N(t+s) - N(t)$ (在时间区间 $(t, T+s]$ 上到达的个数) 独立于 $\{N(u), 0 \leq u \leq t\}$； - 对于所有 $t, s \ge 0$，分布 $N(t+s) -N(t)$ 独立于 $t$。

the number of arrivals in the interval (t, t 1 s] is independent of the number of arrivals in the earlier time interval [0, t] and also of the times at which these arrivals occur

The following theorem, 定理1: 如果 $\{N(t), t\ge 0\}$ 是一个泊松过程，那么在长度为 $s$ 的任意时间区间上到达的数目是参数为 $\lambda s$ ( $\lambda$ 为正实数) 的柏松随机变量。即： \[ P\left[N(t+s) - N(t) = k\right] = \frac{e^{-\lambda s} (\lambda s)^k}{k!} \quad k=0, 1,\cdots, \text{and } t,s \ge 0 \] 因此，$\mathbb{E} [N(s)] = \lambda s$ (See Sec 6.2.3 )，且，$\mathbb{E} [N(1)] = \lambda$ 。因此 $\lambda$ 是长度为 1 的任意区间内到达的期望数目，称之为过程的速率。

定理2: 如果 $\{N(t), t\ge 0\}$ 是速率为 $\lambda$ 的泊松过程，那么它对应的到达间隔时间 $A_1, A_2, \cdots$ 为 IID 指数随机变量，均值为 $1/\lambda$.

6.12.2 Nonstationary Poisson Processes

本节讨论普遍使用的具有时变到达速率的到达过程的模型。

随机过程 $\{N(t), t\ge 0\}$ 是一个非平稳泊松过程，如果： - 顾客每次到达一个； - $N(t+s) - N(t)$ 独立于 $\{N(u), 0 \leq u \leq 0 \}$

令 $\Lambda (t) = \mathbb E [N(t)]$，对于所有 $t \ge 0$，如果对于特定的 $t$ 值 $\Lambda (t)$ 可微 (differentiable) ，将 $\lambda(t)$ 为： \[ \lambda (t) = \frac{\operatorname d}{\operatorname d t} \Lambda(t) \] 直观来看，在到达的期望数目大的区间 $\lambda(t)$ 将会很大，分别称 $\Lambda(t)$ 和 $\lambda(t)$ 为非平稳泊松过程的 期望函数 和 速率函数 。

We call L(t) and l(t) the expectation function and the rate function, re-spectively, for the nonstationary Poisson process. 定理3：如果 $\{N(t), t\ge 0\}$ 为具有连续的期望函数 $\Lambda(t)$ 的非平稳泊松过程，那么：

\[ P[N(t+s)-N(t)=k]=\frac{e^{-b(t, s)}[b(t, s)]^k}{k!} \quad \text { for } k=0,1,2, \ldots \text { and } t, s \ge 0 \] 其中，$b(t, s)= \Lambda(t+s) - \Lambda(t) = \int_t^{t+s} \lambda(y) \operatorname d y$, 对于 $[t, t+s]$ 上所有但有限多个点，如果 $\operatorname d (\Lambda(t))/\operatorname d t$ 在 $[t, t+s]$ 上是有界的且如果 $\operatorname d (\Lambda(t))/\operatorname d t$ 存在并连续，那么最后一个等式成立。

T H E O R E M 6 . 3 . If {N(t), t $ 0} is a nonstationary Poisson process with continuous expectation function L(t), then

it does require somewhat arbitrary judgment about the boundaries and widths of the constant-rate time intervals

6.12.3 Batch Arrivals

For some real-world systems, customers arrive in batches, or groups, so that property 1 of the Poisson process and of the nonstationary Poisson process is violated

Let $N(t)$ now be the number of batches of individual customers that have arrived by time $t$

If $X(t)$ is the total number of individual customers to arrive by time $t$, and if $B_i$ is the number of customers in the $i$th batch,

6.13 Assessing the Homogeneity of Different Data Sets

有时分析人员对一个随机现象独立地收集了 $k$ 组观测值，他想知道这些数据集是否同质从而能合并。

Sometimes an analyst collects k sets of observations on a random phenomenon in-dependently and would like to know whether these data sets are homogeneous and thus can be merged 本节讨论同质性的克鲁斯卡-沃尔斯 (Kruskal-Wallis) 假设检验。由于对数据的分布不做假设，这是非参数化检验。

we discuss the Kruskal-Wallis hypothe-sis test for homogeneity.

7. Random-Number Generators

7.1 Introduction

A simulation of any system or process in which there are inherently random components requires a method of generating or obtaining numbers that are random, in some sense.

So as to avoid speaking of “generating random variables,” which would not be strictly correct since a random variable is defined in mathematical probability theory as a function satisfying certain conditions, we will adopt more precise terminology and speak of “generating random variates.” 本章致力于讨论由 $[0, 1]$ 区间上的均匀分布产生随机变数的方法。

This entire chapter is devoted to methods of generating random variates from the uniform distribution on the interval [0, 1];

This prominent role of the U(0, 1) distribution stems from the fact that random vari-ates from all other distributions (normal, gamma, binomial, etc.) and realizations of various random processes (e.g., a nonstationary Poisson process) can be obtained by transforming IID random numbers in a way determined by the desired distribution or process.

One possibility would be to hook up an electronic random-number machine, such as ERNIE, directly to the computer. This has several disadvantages, chiefl y that we could not reproduce a previously generated random-number stream exactly.

Intuitively the midsquare method seems to provide a good scrambling of one number to obtain the next, and so we might think that such a haphazard rule would provide a fairly good way of generating random numbers

In fact, it does not work very well at all. One serious problem (among others) is that it has a strong tendency to degenerate fairly rapidly to zero, where it will stay forever.

A more fundamental objection to the midsquare method is that it is not “random” at all, in the sense of being unpredictable.

Sometimes arithmetic generators are called pseudorandom, an awkward term that we avoid, even though it is probably more accurate.

who developed what is probably still the most widely used class of techniques for random-number

if designed carefully, can produce numbers that appear to be independent draws from the U(0, 1) distribution, in that they pass a series of statistical tests

A “good” arithmetic random-number generator should possess several properties: 一个“好的”算数随机数发生器应当具备以下属性： - 所产生的数字应当呈现出在 $[0,1]$ 区间上是均匀分布的，并且相互之间不应存在相关性；否则仿真的结果将会完全无效； - 从实用的角度来说，我们希望发生器具有速度快，并且不需要过的的存储空间； - 我们要能严格地重复生成一个给定的随机数流，原因至少有二。1）这有时可能使得调试或校验计算机程序更容易；2）我们可能需要使用一组同样的随机数仿真不同的系统以便得到更为精确的比较； - 发生器应当具备有易于长生分开的随机数流； - 我们希望发生器是方便的，即对所有标准的编译器和计算机来说，产生相同的随机数序列。

The ability to create separate streams for a generator is facilitated if there is an effi cient way to jump from the ith random number to the (i 1 k)th random number for large values of k.

Furthermore, most generators now have the facility for multiple streams in some way, especially those generators included in modern simulation packages, satisfying point 4

Unfortunately, there are also some generators that fail to satisfy the uniformity and independence criteria of point 1 above, which are absolutely necessary if one hopes to obtain correct simulation results.

7.2 Linear Congruential Generators

Many random-number generators in use today are linear congruential generators (LCGs), introduced by Lehmer (1951). 整数 $Z_1, Z_2, \cdots$ 序列由下面的迭代公式定义：

\[ Z_i = (a Z_{i-1} +c) \quad \text{(对 $m$ 取模)} \] 其中，$m$ 表示模数 (modulus ), $a$ 表示乘子 multiplier, $c$ 表示增量 increment ，以及 $Z_0$ 表示种子或初始值 seed 都是非负整数。并且，$0<m, a<m, c<m, Z_0<m$.

Immediately, two objections could be raised against LCGs. 线性同余发生器 LCG 的两个缺点： - 所有（伪）随机数发生器共同的问题，即上述公式定义的 $Z_i$ 根本不是真正的随机数。 - $U_i$ 的取值只能是有理值 $0, 1/m, 2/m, \cdots, (m-1)/m$，事实上，$U_i$ 实际只会取其中的一部分，这依赖于 $m, a, c, Z_0$ 之间的规定，以及 $m$ 浮点除的性质。

The length of a cycle is called the period of a generator. For LCGs, Zi depends only on the previous integer $Z_{i_1}$, and since $0 \leq Z_i \leq m-1$, it is clear that the period is at most $m$; if it is in fact $m$, the LCG is said to have full period.

Since large-scale simulation projects can use millions of random numbers, it is manifestly desirable to have LCGs with long periods.

since we are assured that every integer between 0 and m 2 1 will occur exactly once in each cycle, which should contribute to the unifor-mity of the Ui’s. 因为大规榄系统仿真项目可能使用几百万个随机数，显然希望具有长周期的 LCG，进一步，最好是 满周期，因为我们就能保证在每个循环中 $0\sim m一1$ 之间的每个整数將份好出现一次，这会有助于 $U_i$ 的均匀性（但是，即使是满周期的 LCG，按一个循环的段来说，也可能呈现出非均匀性。

所以，了解如何选择参数 $m$、$a$和 $c$。使得相应的 LCG 具有满周期是有用的。下面的定理给出了这种特征描述。

定理7.1 由 LCG 的定义的 LCG 具有全周期，当且仅当下列三个条件成立： 1. $m$ 和 $c$ 能够同时被整除的正整数只有 $1$，即 $m$ 与 $c$ 互质； 2. 如果 $q$ 为整除 $m$ 的素数（只能被 $1$ 和其自身整除），则 $q$ 能整除 $a一1$； 3. 如果 $4$ 整除 $m$，则 $4$ 整除 $a一1$。

定理7.1中的条件（a）通常表述为“m与c互质。”

日者满周期（盐老至心具长周期）示具好的iCC 的一个所杀胡的从

中指出的，希望好的统斗性料

he following theorem, proved by Hull and Dobell (1962), gives such a characterization

we also want good statistical properties (such as apparent independence), computational and storage effi ciency, reproducibility, facilities for separate streams, and portability (see Sec. 7.2.2). 在上述定理中的条件 1，我们知道 $c>0$ （称为混合 LCG）与 $c=0$（称为乘 LCG）将会有不同的表现。

7.2.1 Mixed Generators

most computers and compilers have 32-bit words, the leftmost bit being a sign bit, so b 5 31 and m 5 231 . 2.1 billion

choosing m 5 2b does allow us to avoid explicit division by m on most computers by taking advantage of integer overfl ow

7.2.2 Multiplicative generators

#乘法发生器 #乘LCG

Multiplicative LCGs are advantageous in that the addition of $c$ is not needed, but they cannot have full period since condition (a) of Theorem 7.1 cannot be satisfied

however, it is possible to obtain period $m- 1$ if $m$ and $a$ are chosen carefully

As with mixed generators, it’s still computationally efficient to choose $m = 2^b$ and thus avoid explicit division 与混合发生器一样，取 $m=2^b$，计算效率仍然高且避免显式除法。但是在这种情况下，其周期最多为 $2^{b-2}$，也就是说，$Z_i$ 所能取得数值的个数仅仅为 $0\sim m-1$ 之间所有整数个数的四分之一。

In fact, the period is 2^{b-2} if Z_0 is odd and $a$ is of the form $8k + 3$ or $8k +5$ for some $k=0, 1, \cdots$

he generator usually known as RANDU is of this form ($m=2^{31}, a = 2^{16}+3=65 539, c=0$) and has been shown to have very undesirable statistical properties (see Sec. 7.4). 普遍熟知的发生器 RANDU 就是这样的形式，即 $m=2^{31}, a = 2^{16}+3=65 539, c=0$，而且已经证明，这个发生器具有 不尽如人意的统计特性。

Because of these difficulties associated with choosing $m = 2^b$ in multiplicative LCGs, attention was paid to finding other ways of specifying $m$. 由于在乘 LCG 中选 $m=2^b$ 带来的这些困难，人们将注意力放在寻找其他方法来规定 $m$ 值。不是令 $m=2^b$，而建议 $m$ 取小于 $2^b$ 的最大素数。例如，在 $b=31$ 的情形，小于 $2^{31}$ 的最大素数非常容易得到 $2^{31}—1=2147483647$。现在，对于素数$m$，可以证明，如果 $a$ 为模 $m$ 的素元 (primitive element modulo)，则周期为 $m一1$，即使 $a^l -1$ 能被 $m$ 整除的最小整数是 $l=m-1$。

对于以这种方法选择的 $m$ 和 $a$，我们得到每个整数 $1，2, \cdots，m-1$ 在每个循环内正好出现一次，所以 $Z_0$ 可以是 $1 \sim m一1$ 的任意整数，得到的周期仍是 $m-1$。这称为素数取模乘 LCG（ prime modulus multiplicative LCGs, PMMLCGs)。

These are called prime modulus multiplicative LCGs (PMMLCGs)

Two issues immediately arise concerning PMMLCGs: 与 PMMLCGs 相关的两个问题随即产生： 1. 如何得到模 $m$ 的素元？将通过讨论下面两个广泛使用的 PMMLCG 在本质上解决这一点； 2. 由于不选 $m=2^b$，再也不能直接使用 整数溢出 机制来达到取 $m$ 模除法的效果。这种情况下，避免显式除法的方法也适用一类溢出，称为 仿真除 ( simulated division)。

Considerable work has been directed toward identifying good multipliers a for PMMLCGs t

Two particular values of a that have been widely used for the modulus m* are $a_1 = 7^5 = 16807$ and $a_2 = 630,360,016$, both of which are primitive elements modulo m* 对于模数 $m^*$，已经取得广泛使用的 $a$ 的两个特定乘数值为 $a_1 = 7^5 = 16807$ 和 $a_2 = 630,360,016$, 这两个都是取模 $m^*$ 的素元。

The multiplier a1 was originally suggested by Lewis, Goodman, and Miller (1969), and it was used by Schrage (1979) in a clever FORTRAN implementation using simulated division. The importance of Schrage’s code was that it provided at that time a reasonably good and portable random-number generator.

However, many experts [see, e.g., L’Ecuyer, Simard, Chen, and Kelton (2002) and Gentle (2010, p. 21)] recommend that LCGs with a modulus of around 231 should no longer be used as the random-number generator in a general-purpose software package

Not only can the period of the generator be exhausted in a few minutes on many computers, but, more importantly, the relatively poor statistical properties of these generators can bias simulation results for sample sizes that are much smaller than the period of the generator 不建议作为通用仿真软件包中的随机数发生器： 1. 一个周期的随机数在很多计算机上往往在几分钟内就被用尽； 2. 这些随机数相对较差的统计性会使得仿真结果偏离样本长度，后者较发生器周期要小很多。

7.3 Other Kinds of Generators

Although LCGs are probably the most widely used and best understood kind of random-number generator, there are many alternative types. 开发其他类型发生器的主要目的是要得到更长的周期和更好的统计特性。

7.3.1 More General Congruences

LCGs can be thought of as a special case of generators defined by:

\[ Z_i = g(Z_{i-1}, Z_{i-2}, \cdots) (\operatorname{mod}m) \] where $g$ is a fixed deterministic function of previous $Z_j$'s.

两种推广： - 二次同余发生器 (quadratic congruential generator) - 多重递归发生器 (multiple recursive generator, MRG)

One obvious generalization of LCGs would be to let g(Zi21, Zi22, . . .) 5 a9Z2i21 1 aZi21 1 c, which produces a quadratic congruential generator

A different choice of the function g is to maintain linearity but to use earlier Zj’s; this gives rise to generators called multiple recursive generators (MRGs)

7.3.2 Composite Generators

Several researchers have developed methods that take two or more separate genera-tors and combine them in some way to generate the fi nal random numbers. 复合发生器：将两个或多个单独的发生器以某种方式结合起来生成最终的随机数。期望这种组合发生器较之组成它的任何单个发生器有更长的周期，更好地统计性能。缺点：代价大于单独使用一个发生器。

The disadvantage in using a composite generator is, of course, that the cost of obtaining each $U_i$ is more than that of using one of the simple generators alone.

Wichmann and Hill (1982) proposed the following idea for combining three generators, again striving for long period, portability, speed, and usability on small computers

7,3,3 Feedback Shift Register Generators

线性反馈移位寄存器 (Linear feedback shift register, LFSR)

The original motivation for suggesting that the bi’s be used as a source of U(0, 1) random numbers came from the observation that the recurrence given by Eq. (7.4) can be implemented on a binary computer using a switching circuit called a linear feedback shift register (LFSR)

Unfortunately, LFSR generators are known to have statistical defi ciencies, - 广义反馈移位寄存器 (Generalized feedback shift register, GFSR) - 旋转的广义反馈移位寄存器 (twisted generalized feedback shift register, TGFSR)

With suitable choices for $r$, $q$, and $A$, a TGFSR generator can have a maximum period of $2^{ql}-1$ as compared with $2^{q}-1$ for a GFSR generator (both require $ql$ bits to store the state of the generator).

7.4 Testing Random Number Generators

As we have seen in Secs. 7.1 through 7.3, all random-number generators currently used in computer simulation are actually completely deterministic. Thus, we can only hope that the $U_i$’s generated appear as if they were IID $U(0, 1)$ random variates

Before such a generator is actually used in a simulation, we strongly recommend that one identify exactly what kind of generator it is and what its nu-merical parameters are.

7.4.1Empirical Tests

Perhaps the most direct way to test a generator is to use it to generate some $U_i’$s, which are then examined statistically to see how closely they resemble IID $U(0, 1)$ random variates 本节将讨论四种实验检验方法，统计检查随机数类似 $U(0, 1)$ 随机数的紧密程度。 1. 所有参数已知的 $\chi^2$ 检验的特殊情形； 2. 连续检验，实际上是把 $\chi^2$ 检验推广到高维； 3. 游程（或上升游程）检验，是对独立性假设的更直接检验（实际上，它只检验独立性，即把特别是不检验均匀性）； 4. 用直接的方法以评价所产生的 $U_i$ 是否存在可辨别的相关性：对于某个 $l$，只计算其滞后 $j = 1,2,\cdots$ 的滞后 $j$ 的相关系数的估计。

Why should we care about this kind of uniformity in higher dimensions? If the individual $U_i$’s are correlated, the distribution of the d-vectors $U_i$ will deviate from $d$-dimensional uniformity; thus, the serial test provides an indirect check on the assumption that the individual $U_i$’s are independent.

The third empirical test we consider, the runs (or runs-up) test, is a more di-rect test of the independence assumption.

As mentioned above, these are just four of the many possible empirical tests. For example, the Kolmogorov-Smirnov test discussed in Sec. 6.6.2

RANDU is a fatally fl awed generator, due primarily to its utter failure in three dimensions;

One potential disadvantage of empirical tests is that they are only local; i.e., only that segment of a cycle (for LCGs, for example) that was actually used to generate the Ui’s for the test is examined, so we cannot say anything about how the generator might perform in other segments of the cycle. 实验检验的缺陷：他们总是局部的，也就是说，仅仅对循环中的一段进行了检验，这一段实际上是用于产生检验用的 $U_i$。

7.4.2 Theoretical Tests

We now discuss theoretical tests for random-number generators. Since these tests are quite sophisticated and mathematically complex, we shall describe them somewhat qualitatively;

as mentioned earlier, theoretical tests do not re-quire that we generate any $U_i$’s at all but are a priori in that they indicate how well a generator can perform by looking at its structure and defining constant

Theoretical tests also differ from empirical tests in that they are global; i.e., a genera-tor’s behavior over its entire cycle is examined.

global tests have a natural appeal but do not generally indicate how well a specifi c segment of a cycle will behave

7.4.3 Some General Observations on Testing

One piece of advice that is often offered, however, is that a random-number generator should be tested in a way that is consistent with its intended use.

8. Generating Random Variables

8.1 Introduction

A simulation that has any random aspects at all must involve sampling, or generat-ing, random variates from probability distributions.

These distri-butions are often specifi ed as a result of fi tting some appropriate distributional form, e.g., exponential, gamma, or Poisson, to observed data, as discussed in Chap. 6

we address the issue of how we can gen-erate random variates with this distribution in order to run the simulation model.

the basic ingredient needed for every method of generating random variates from any distribution or random process is a source of IID $U(0, 1)$ random variates

Without an ac-ceptable random-number generator, it is impossible to generate random variates correctly from any distribution

several factors should be considered when choosing which algorithm to use in a particular simulation study. Unfortu-nately, these different factors often confl ict with each other, so the analyst’s judg-ment of which algorithm to use must involve a number of tradeoffs 选择什么算法来生成随机变量，应该考虑多种因素： - 准确性 - 效率 - 复杂性 - 技术

The fi rst issue is exactness. We feel that, if possible, one should use an algo-rithm that results in random variates with exactly the desired distribution, within the unavoidable external limitations of machine accuracy and exactness of the U(0, 1) random-number generator

Given that we have a choice, then, of alternative exact algorithms, we would clearly like to use one that is effi cient, in terms of both storage space and execution time.

A somewhat subjective issue in choosing an algorithm is its overall complexity, including conceptual as well as implementational factors.

Finally, there are a few issues of a more technical nature. Some algorithms rely on a source of random variates from distributions other than U(0, 1), which is unde-sirable, other things being equal.

used variance-reduction techniques (common random numbers and antithetic vari-ates) require synchronization of the basic U(0, 1) input random variates used in the simulation of the system(s) under study, and this synchronization is more easily accomplished for certain types of random-variate generation algorithms

generat-ing correlated random variates and generating realizations of both stationary and non-stationary arrival processes

8.2 General Approaches to Generating Random Variates

There are many techniques for generating random variates, and the particular algorithm used must, of course, depend on the distribution from which we wish to generate; however, nearly all these techniques can be classifi ed according to their theoretical basis

8.2.1 Inverse Transform

Then an algorithm for generating a random variate $X$ having distribution function $F$ is as follows (recall that , $\sim$ is read “is distributed as”): 假定要产生一个连续随机变量 $X$ (See Sec 4.2)，$X$ 有分布函数 $F$，当 $0<F(x)<1$ 时，$F$ 是连续的且严格递增的（这意味着如果 $x_1 < x_2$ 且 $0 < F(x_1) \leq F(x_2) < 1$ ，则事实上 $F(x_1) < F(x_2)$）。

令 $F^{-1}$ 表示函数 $F$ 的逆，则生成具有分布函数 $F$ 的随机变量 $X$ 的算法如下： 1. 产生 $U \sim U(0,1)$ 2. 返回 $X = F^{-1}(U)$

通用反变换法 (General inverse-transform method)

To show that the value X returned by the above algorithm, called the general inverse-transform method, - Transformer uniform distribution to exponential distribution

eg.1 令 $X$ 具有均值为 $\beta$ 的指数分布，其分布函数为： \[ F(x)=\left\{ \begin{array}{ll} 1-e^{-x / \beta} & \text { if } x \ge 0 \\ 0 & \text { otherwise } \end{array} \right. \] 则为得到 $F^{-1}$，设 $u = F(x)$ 并求解 $x$，以得到： \[ x = F^{-1}(u) = - \beta \ln(1-u) \] 因此，要生成所要求的随机变量，首先生成一个 $U \sim U(0,1)$，而后令 $X = -\beta \ln U$。

The inverse-transform method’s validity in the continuous case was demon-strated mathematically above, but there is also a strong intuitive appeal

The inverse-transform method can also be used when X is discrete.

Generalization, Advantages, and Disadvantages of the Inverse-Transform Method

Let us now consider some general advantages and disadvantages of the inverse-transform method in both the continuous and discrete cases. 反变换法的缺点： - 在连续情况下应用这种方法可能的问题是需要计算 $F^{-1}(U)$，由于无法以闭合形式写出所要求的分布的 $F^{-1}$ 的公式（如正态分布和伽马分布），因此有时候简单的反变换法不一定可行； - 对于给定分布，反变换法或许不是生成相应随机变量的最快速方法。

优点： - 易于使用方差缩减技术。依赖于引进随机变量间的相关性，如公共随机数法和对偶变量法 ( antithetic variates) - 易于从截断分布中产生随机变量。

Despite these possible drawbacks, there are some important advantages in using the inverse-transform method.

Then an algorithm for generating an X having dis-tribution function F* is as follows:

8.2.2 Composition

The composition technique applies when the distribution function $F$ from which we wish to generate can be expressed as a convex combination of other distribution functions $F_1, F_2, \cdots$. We would hope to be able to sample from the $F_j$’s more easily than from the original $F$

8.2.3 Convolution

For several important distributions, the desired random variable $X$ can be expressed as a sum of other random variables that are IID and can be generated more readily than direct generation of $X$.

X is called the m-fold convolution of the distribution of a $Y_j$. 组合法和卷积法的区别： - 卷积法：假定随机变量 $X$ 可以表示为其他随机变量的和‘ - 组合法：假设 $X$ 的 分布函数 可以表示为其他分布函数的 （加权）和

Convolution is really an example of a more general idea, that of transforming some intermediate random variates into a fi nal variate that has the desired distribu-tion;

8.2.4 Acceptance-Rejection

前面三种方法（反变换法、组合法和卷积法）都是直接方法，即直接面对所要求的分布或随机变量。而可用于 直接方法无效或者效率不佳 的情形的方法： - 舍取法 另外两种方法： - 均匀比法 - 特性法

The principle of acceptance-rejection is quite general, and looking at the above algorithm in a slightly different way clarifi es how it can be extended to generation

8.3 Generating Continuous Random Variates

In this section we discuss particular algorithms for generating random variates from several commonly occurring continuous distributions;

n deciding which algorithm to present, we have tried to choose those that are simple to describe and implement, and are reasonably effi cient as well. We also give only exact (up to machine accuracy) methods, as opposed to approximations 1. Uniform 均匀分布

8.3.1 Uniform 2. Exponential

8.3.2 Exponential 3. $m$-Erlang

8.3.3 m -Erlang

Fortunately, the m-Erlang dis-tribution is a special case of the gamma distribution (with shape parameter a equal to the integer m), so that we can use one of the methods for generating gamma ran-dom variates here as well (see Sec. 8.3.4 for discussion of gamma generation). 4. Gamma

8.3.4 Gamma 5. Weibull

8.3.5 Weibull 6. Normal

8.3.6 Normal

It does have the advantage, however, of maintaining a one-to-one correspondence between the random numbers used and the N(0, 1) random vari-ates produced

there is a serious diffi culty if $U_1$ and $U_2$ are actually adjacent random numbers produced by a linear congruential generator (see Sec. 7.2), 极坐标法 Polar method

An improvement to the Box and Muller method, which eliminates the trigono-metric calculations and was described in Marsaglia and Bray (1964), has become known as the polar method 7. Lognormal

8.3.7 Lognormal 8. Beta

8.3.8 Beta

8.4 Generating Discrete Random Variates

discusses particular algorithms for generating random variates from various discrete distributions that might be useful in a simulation study

The discrete inverse-transform method, as described in Sec. 8.2.1, can be used for any discrete distribution, whether the range of possible values is fi nite or (count-ably) infi nite - 别名法 (alias method)

One other general approach should be mentioned here, which can be used for generating any discrete random variate having a fi nite range of values. This is the alias method, 1. Bernoulli 2. Discrete Uniform 3. Arbitrary Discrete Distribution 4. Binomial 5. Geometric 6. Negative Binomial 7. Poisson

Although the alias method is limited to discrete random variables with a fi nite range, it can be used indirectly for discrete distributions with an infi nite range, such as the geometric, negative binomial, or Poisson

8.5 Generating Random Vectors, Correlated Random Variates, and Stochastic Processes

So far in this chapter we have really considered generation of only a single random variate at a time from various univariate distributions 本章到目前为止，实际考虑的只是从各种 单变量 分布中每次产生单个随机变量。利用随机数组重复应用这些方法的一种由所要求的分布产生一串独立同分布的随机变量。

Using Conditional Distributions

As general as this approach may be, its practical utility is probably quite limited. 2. Multivariate Normal and Multivariate Lognormal

Since $\Sigma$ is symmetric and positive definite, we can factor it uniquely as $\Sigma = CC^T$ (called the Cholesky decomposition), where the $d \times d$ matrix $C$ is lower triangular

Note that $\mu$ and $\Sigma$ are not the mean vector and covariance matrix of the desired multivariate lognormal random vector $X$, but rather are the mean and covariance matrix of the corresponding multivariate normal random vector $Y$. 3. Correlated Gamma Random Variates

we cannot write the entire joint distribution but only specify the marginal distributions (gamma) and the correlations between the com-ponent random variables of the $X$ vector. 4. Generating from Multivariate Families 5. Generating Random Vectors with Arbitrarily Specified Marginal Distributions and Correlations

we noted the need to model some input random variables as a random vector with fairly arbitrary marginal distributions and correlation structure, rather than specifying and controlling their entire joint distribution as a member of some multivariate parametric family like normal, lognormal, Johnson, or Bézier

The only constraint is that the correlation structure between them be inter-nally consistent with the form and parameters of the marginal distributions, as dis-cussed by Whitt (1976), i.e., that the correlation structure specifi ed be feasible

They present specifi c examples through dimension d 5 3 when the marginal distributions are uniform, exponential, and discrete uniform 6. Generating Stochastic Processes

some applications require that we generate observa-tions of the “same” random variable as it is observed through time. 常见随机过程的产生： - AR 和 ARMA 过程 - 伽马过程 - ARTA 过程 - VARTA 过程

8.6 Generating Arrival Processes

泊松过程
非平稳泊松分布

9. Output Data Analysis for a Single System

9.1 Introduction

As a matter of fact, a common mode of operation is to make a single simulation run of somewhat arbitrary length and then to treat the resulting simulation estimates as the “true” model characteristics.

9.2 Transient and Steady-state Behavior of a Stochastic Process

For fixed $y$ and $I$, the probabilities $F_1(y|I), F_2(y|I ), \cdots$ are just a sequence of numbers. If $F_i( y|I)$ as $i\to \infty$ for all $y$ and for any initial conditions $I$, then $F(y)$ is called the steady-state distribution of the output process $Y_1, Y_2, \cdots$, Note：稳态并不意味着在一次特定的仿真中随机变量 $Y_{k+1}, Y_{k+2}, \cdots$ 都取相同的值，而是意味着它们都 近似地 具有相同的分布。进一步，这些随机变量之间并不独立，但近似一个 方差平稳 的随机过程。

9.3 Types of Simulations with Regard to Output Analysis

The options available in designing and analyzing simulation experiments depend on the type of simulation at hand, as depicted in Fig. 9.4 - 终止型仿真 terminating simulation

The event E often occurs at a time point when the system is “cleaned out” (see Example 9.4), at a time point beyond which no useful information is obtained (see Example 9.5), or at a time point specifi ed by management mandate - 非终止型仿真 nonterminating simulation

A nonterminating simulation is one for which there is no natural event E to specify the length of a run.

It should be mentioned that stochastic processes for most real systems do not have steady-state distributions, since the characteristics of the system change over time

On the other hand, a simulation model (which is an abstraction of reality) may have steady-state distributions, since characteristics of the model are often assumed not to change over time. When we have new information on the characteristics of the system, we can redo our steady-state analysis.

For a nonterminating simulation, suppose that the stochastic process Y1, Y2, . . . does not have a steady-state distribution, and that there is no appropriate cycle defi -nition such that the corresponding process Y1C, Y2C, . . . has a steady-state distribu-tion

In these cases, however, there will typically be a fi xed amount of data describing how input parameters change over time

9.4 Statistical Analysis for Terminating Simulations

Suppose that we make $n$ independent replications of a terminating simulation, where each replication is terminated by the event $E$ and is begun with the “same” initial conditions - Obtaining a specified precision

One disadvantage of the fixed-sample-size procedure based on n replications is that the analyst has no control over the confidence-interval half-length (or the precision of $X(n)$); for fixed $n$, the half-length will depend on Var($X$), the population variance of the $X_j$’s