This blog is the learning notes for preparing the preliminary exams of Queue theory, referring to Fundamentals of supply chain theory.

Snyder, L. V., & Shen, Z. J. M. (2019). Fundamentals of supply chain theory. John Wiley & Sons.

1. Introduction

1.1 The Evolution of Supply Chain Theory

Supply chains used to be viewed, at least by some managers, as “necessary evils.”

By the end of the last century, however, the purpose of the supply chain had begun to change as some firms discovered that supply chains could be a source of competitive advantage, rather than simply a cost driver.

The final chapter of this book is devoted to exploring how the tools of supply chain theory are used in a few of these application areas—electricity systems, health care, and public sector operations.

Note: 本文文字部分借助 obsidian + Annotator 插件（Annotator 介绍见 obsidian-annotator)，实现 pdf 文档标注及文字时时提取功能，能够将所有标注的文字提取到 markdown 文件中。图片部分借助 Image auto upload plugin 插件（见 Link ）和 PicGo 实现图片自动上传到 GitHub 图床。然后借助 python 实现简单的文本内容提取，就可以得到纯净的笔记内容。具体操作和实现流程，见之前博客Photography-is-simple/的引言部分教程。

完整笔记链接见： Download Now

1.2 Definiton and Scope

Perhaps the most authoritative definition comes from the Council of Supply Chain Management Professionals(CSCMP), who define supply chain management as follows

Supply chain management encompasses the planning and management of all activities involved in sourcing and procurement, conversion, and all logistics management activities. Importantly, it also includes coordination and collaboration with channel partners, which can be suppliers, intermediaries, third party service providers, and customers. In essence, supply chain management integrates supply and demand management with in and across companies

These practices include a huge range of tasks, such as forecasting, production planning, inventory management, warehouse location, supplier selection, procurement, and shipping.

The terms “logistics” and “logistics management” are closely related to “supply chain management,” and it can be difficult to draw a clear distinction.

“supply chain management” includes logistics, as well as nonmovement activities such as inventory management and procure-ment.

Supply chains are often represented graphically as a schematic network that illustrates the relationships between its elements

A location in the network is referred to as a stage or node. The links between stages represent some type of flow—typically, the flow of goods, but sometimes the flow of information or money

The portion of the supply chain from which products originate (the left-hand portion in Figure 1.1) is referred to as up stream, while the demand end is referred to as downstream.

But today’s supply chains more closelyresemble the complex network in Figure 1.1; each echelon may have dozens, hundreds,or even thousands of nodes.

The ideal supply chain management model would globally optimize every aspect of thesupply chain, but such a model is impossible both because of the difficulties in modelingsome aspects of the supply chain mathematically and because the resulting model wouldbe too large and complex to solve

1.3 Levels of Decision-making in Supply Chain Management

It is convenient to think about three levels of supply chain management decisions: strategic,tactical, and operational. Three level of supply chain management decisions: - strategic - tactical - operational

2. Forecasting and Demad Modeling

2.1 Introduction

Demand forecasting is one of the most fundamental tasks that a business must perform Advantage: - Improving customer service levels and by reducing costs related to supply–demand mismatches. Disadvantage - biased or otherwise inaccurate forecasting results in inferior decisions and thus undermines business performance.

The goal of the forecasting models discussed in this chapter is to estimate the quantityof a product or service that consumers will purchase

Most classical forecasting techniquesinvolve time-series methods that require substantial historical data. Some of these methodsare designed for demands that are stable over time

However, products today have shorter and shorter life cycles, in part driven by rapidtechnology upgrades for high-tech products. As a result, firms have much less historicaldata available to use for forecasting, and any trends that may be evident in historical datamay be unreliable for predicting the future - Large quantities of historical data available.

n Section 2.4, we discuss more recent approaches to forecastingdemand using machine learning when we have large quantities of historical data available - Inadequate historical data

n Sections 2.5–2.8, we discuss several methods that can be used to predict demands for newproducts or products that do not have much historical data.

To distinguish these methodsfrom classical time-series–based methods, we call them demand modeling techniques. Demand modeling techniques: - Quantitative

They all involve mathe-matical models with parameters that must be calibrated. - Some popular methods

In contrast, some popular methodsfor forecasting demand with little or no historical data, such as the Delphi method, rely onexperts’ qualitative assessments or questionnaires to develop forecasts. Demand processes may exhibit various forms of nonstationarity over time. These include the following:
- Trends: Demand consistently increases or decreases over time.
- Seasonality: Demand shows peaks and valleys at consistent intervals.
- Product life cycles: Demand goes through phases of rapid growth, maturity, and decline.

Moreover, demands exhibit random error—variations that cannot be explained or predicted—and this randomness is typically superimposed on any underlying nonstationarity superimpose: vt. 使重叠,使叠加

Classical forecasting methods use prior demand history to generate a forecast.

assume that pastpatterns of demand will continue into the future, that is, no trend is present. As a result, these techniques are best used for mature products with a large amount of historical data

On the other hand, regression analysis and double and triple exponential smoothing canaccount for a trend or other pattern in the data.

2.2.1 Moving Average

The moving average method calculates the average amount of demand over a given intervalof time and uses this average to predict the future demand. The definition of Moving Average: \[ D_t = I + \epsilon_t \] where $I$ is the mean or "base" demand and $\epsilon$ is a random error term.

$ most recent observed demands.== %%POSTFIX%%Theforecast for the demand in p*

That is, the forecast is simply the arithmetic mean of the previous N observations. This isknown as a simple moving average forecast of order N.

2.2.2 Exponential Smoothing

Exponential smoothing is a technique that uses a weighted average of all past data as thebasis for the forecast. Assumption: - Single exponential smoothing: the demand process is stationary; - Double exponential smoothing: there is a trend; - Triple exponential smoothing: account for trends and seasonality.

These methods all requireuser-specified parameters that determine the relative weights placed on recent and olderobservations when predicting the demand, trend, and seasonality These three weights arecalled, respectively, the smoothing factor, the trend factor, and the seasonality factor 1. Single Exponential Smoothing

The single exponential smoothing forecast includes all pastobservations, These weights can be approximated with an exponential function $f(i) = αe^{−αi}$. 2. Double Exponential Smoothing

Double exponential smoothing can beused to forecast demands with a linear trend.

It places a weight of $β$ on the most recent estimate of the slope(obtained by taking the difference between the two most recent base signals) and a weight of $1 −β$ on the previous estimate 3. Triple Exponential Smoothing

Triple exponential smoothing can be usedto forecast demands that exhibit both trend and seasonality. Seasonality: the demand series has a pattern that repeats every $N$ periods for some fixed $N$.

The idea behind smoothing with trend and seasonality is basically to “de-trend” and “de-seasonalize” the time series by separating the base signal from the trend and seasonalityeffects

Initializing triple exponential smoothing is a bit trickier than for single or double expo-nential smoothing.

To do so, we usually need at least two entire seasons’ worth of data($2N$ periods), which will be used for the initialization phase. One common method is toinitialize the slope as

In other words, we take the per-period increase in demand between periods 1 and $N + 1$, and the per-period increase between periods 2 and $N + 2$, and so on; and then we take the average over those $N$ values.

2.2.3 Linear Regression

Historical data can also be used to forecast demands by determining a cause–effect rela-tionship between some independent variables and the demand

In linear regression, the model specification assumes that the dependent variable, Y , is alinear combination of the independent variables.

To build a regression model, we need historical data points—observations of both theindependent variable(s) and the dependent variable.

2.3 Forecast Accuracy

2.3.1 MAD, MSE and MAPE

Measurements: - MAD: Mean Absolute Deviation - MSE: Mean Squared Error - MAPE: Mean Absolute Percentage Error

\[ \begin{aligned} \mathrm{MAD} & =\frac{1}{n} \sum_{t=1}^n\left|e_t\right| \\ \mathrm{MSE} & =\frac{1}{n} \sum_{t=1}^n e_t^2 \\ \mathrm{MAPE} &= \frac{1}{n} \sum\limits_{t-i}^{n} \left| \frac{e_t}{D_t}\right| \times 100 \end{aligned} \]

If the mean of the forecast error, μe,equals 0, we say the forecasting method is unbiased: It does not produce forecasts that aresystematically either too low or too high.

MAD is sometimes preferred to MSE in real applicationsbecause it avoids the calculation of squaring, though modern spreadsheet and statisticspackages can compute either performance measure easily.

2.4 Machine Learning in Demand Forecasting

2.4.1 Introduction

The huge volume of data generated every day, the high velocityof data creation, and the large variety of sources all make today’s business informationenvironment different than it was only a decade ago.

Compared with classical forecastingmethods such as the time series methods discussed in Section 2.2, machine learning modelsoften significantly increase prediction accuracy.

2.4.2 Machine Learning

machine learning (ML) refers to a set of algorithms that can learn from andmake predictions about data

Both techniques fall into the overall field of data science, which covers a wider range oftopics, including database design and data visualization techniques.

In contrast, unsupervised learning explores relationships and structures withinthe data without any known “ground truth” labels or outputs.

Common supervised learning methods include linear regression (and its nonlinear ex-tensions), kernel methods, tree-based models, support vector machines (SVMs), and neuralnetworks

Graphical models involving hidden Markov models (or, in their simplest form,mixture models) and Markov random fields also receive considerable attention. 1. Linear regression 2. Tree-based models

The trees used for these two types of problems are referred to as regression treesand classification trees, respectively. In demand forecasting, regression trees have receivedmore attention because of their simplicity and interpretability

However, in practice, the number of possible partitionsmay be too large to enumerate. Therefore, it is common to use a binary splitting methodcalled recursive partitioning, which generates two regions from the original region at eachiteration.

researchershave developed methods that combine several trees to enhance the prediction performance.These include random forests, bagging, and boosting.

stock-keeping unit (SKU) sales 3. Support vector machines

SVMs are designed to partition the space ofinput variables into two regions, i.e., to make a binary prediction about a given outputbased on which region a given input vector falls into.

SVMs can be generalized to allow nonlinearities by mapping the input space into ahigh-dimensional space using kernel functions.

Popular choices ofkernel functions include polynomials and radial basis functions (RBFs) 4. Neural networks

A neural network consists of several nodes, also calledneurons, arranged into layers.

The key challenge in fitting a neural network model is the determination of the weights $\alpha_{0m}$ and $\alpha_m$. This is usually done using some sort of algorithm that modifies the weights as the network “learns” right and wrong answers.

Suchdeep neural networks have led to huge advances in machine learning, with great successesnot only in classification and prediction problems such as image processing and demandforecasting, but also, when coupled with reinforcement learning (RL), in solving decisionproblems such as those in board games

2.5 Demand Modeling Techniques

they need tounderstand the life cycles and demand dynamics of their products

It turns outthat classical forecasting techniques did not work well with the company’s highly variable,short-life-cycle products, so the firm introduced products at the wrong times in the wrongquantities.

2.6 Bass Diffusion Model

The sales patterns of new products typically go through three phases: rapid growth, maturity,and decline

The premise of the Bass model is that customers can be classified into innovatorsand imitators.

Thegoal of the Bass model is to characterize this behavior in an effort to forecast the demand

Moreover, it attempts topredict two important dimensions of a forecast: how many customers will eventually adoptthe new product, and when they will adopt

Knowing the timing of adoptions is importantas it can guide the firm to smartly utilize resources in marketing the new product.

2.6.1 The Model

It assumes that $P(t)$, the probability that a given buyer makes an initial purchase at time $t$ given that she has not yet made a purchase, is a linear function of the number of previous buyers, that is, \[ P(t) = p + \frac{q}{m} D(t) \] where $D(t)$ is the cumulative demand by time $t$. $q$ and $m$ represent the coefficient of imitation and the market size.

This equation include two influence factors: - coefficient of innovation, denoted $p$, which is a constant, independent of how many other customers have adopted the innovation before time $t$. - the "contagion" effect between the innovators and the imitators, denoted $\frac{q}{m} D(t)$, which is proportional to the number of customers who have already adopted by time $t$.

Our preference would be to have a closed-form expressionfor D(t). Fortunately, this is possible:

In summary, by varying the values of p and q, we can represent manydifferent patterns of demand diffusion

2.6.2 Discrete Time Version

A discrete-time version of the Bass model is available.

2.6.3 Parameter Estimation

The Bass model is heavily driven by the parameters $m$, $p$, and $q$.

However, because the Bass model is typically used for new products, in most caseshistorical data are not available to estimate the parameters.

Instead, m is typically esti-mated qualitatively, using judgment or intuition from management about the size of themarket, market research, or the Delphi method

The parameters $p$ and $q$ tend to be relatively consistent withina given industry, so these can often be estimated from the diffusion patterns of similarproducts.

2.6.4 Extensions

The original model has also been extendedin a number of ways.

2.7 Learning Indicator Approach

Product life cycles are becoming shorter and shorter, so it is difficult to obtain enoughhistorical data to forecast demands accurately. - Solution: leading indicators

One idea that has proven to work well insuch situations is the use of leading indicators—products that can be used to predict thedemands of other, later products because the two products share a similar demand pattern

The idea is first to group the products into clusters so that all of the products within a clustershare similar attributes.

Even though all of the products are on the market simultaneously,the lag provides enough time so that supply chain planning for the products in the clustercan take place based on the forecasts provided by the leading indicator. Of course, correctlyidentifying the leading indicator is critical.

2.8 Discrete Choice Models

2.8.1 Introduction to Discrete Choice

In economics, discrete choice models involve choices between two or more discrete alterna-tives

The idea behind discrete choice models is to build a statistical model that predictsthe choice made by an individual based on the individual’s own attributes as well as theattributes of the available choices.

choice models are atthe aggregate (population) level and assume that each decision-maker’s preferences arecaptured implicitly by that model.

Discrete choice models take many forms, including binary and multinomial logit, binaryand multinomial probit, and conditional logit.

For a discrete choice model, the setof alternatives in the choice set must be mutually exclusive, exhaustive, and finite.

Discrete choice models usuallyassume that the decision-maker is a utility maximizer. That is, he will choose alternative iif and only if $U_{ni} > U_{nj}$ for all $j ∈I, j \neq i$

2.8.2 The Multinomial Logit Model

Next we derive the multinomial logit model. (Refer to McFadden (1974) or Train (2009)for further details of the derivation.) “Multinomial” means that there are multiple optionsfrom which the decision-maker chooses

3. Deterministic Inventory Models

3.1 Introduction to Inventory Modeling

These are all reasons that firms plan to hold inventory. In addition, firms may holdunplanned inventory—for example, inventory of products that have become obsolete soonerthan expected

In fact, although we tend todiscuss inventory models as though the firm is buying a product from an outside supplier,most inventory models apply equally well to production systems,

Mathematical inventory models can be classified along a number of different dimensions: Mathematical inventory models can be classified along a number of different dimensions: - Demand - Lead time - Review type - Planning horizon - Stockout type - Ensuring good service - Fixed cost - Perishability

Like all mathematical models, inventory models must balance two competing factors—realism and tractability

The goal of most inventory models is to minimize the cost (or maximize the profit) of theinventory system. Four types of costs: - Holding cost - Fixed cost - Purchase cost - Stockout cost

Stockout cost. This is the cost of not having sufficient inventory to meet demand, alsocalled the penalty cost or stockout penalty

There are several measures that we use to assess the amount of inventory in the system atany given time. There are several measures that we use to assess the amount of inventory in the system at any given time. - On-hand inventory (OH) refers to the number of units that are actually available at the stocking location. - Backorders (BO) represent demands that have occurred but have not been satisfied. Generally, it’s not possible for the on-hand inventory and the backorders to be positive at the same time - The inventory level (IL) is equal to the on-hand inventory minus backorders - inventory position (IP), which equals the inventory level plus items on order

the economic order quantity (EOQ) model, perhaps the oldest and best-known mathematical inventory model (Section 3.2), and some of its extensions; and thena periodic-review model

The models discussed in this chapter are sometimes known as economic lot size problems.

3.2 Continuous Review: The Economic Order Quantity Problem

3.2.1 Problem Statement

The economic order quantity (EOQ) problem is one of the oldest and most fundamentalinventory models; it was first introduced by Harris (1913). The goal is to determine theoptimal amount to order each time an order is placed to minimize the average cost per year.

Any optimal solution for the EOQ model has two important properties: Any optimal solution for the EOQ model has two important properties: 1. Zero-inventory ordering (ZIO) property; 2. Constant order sizes.

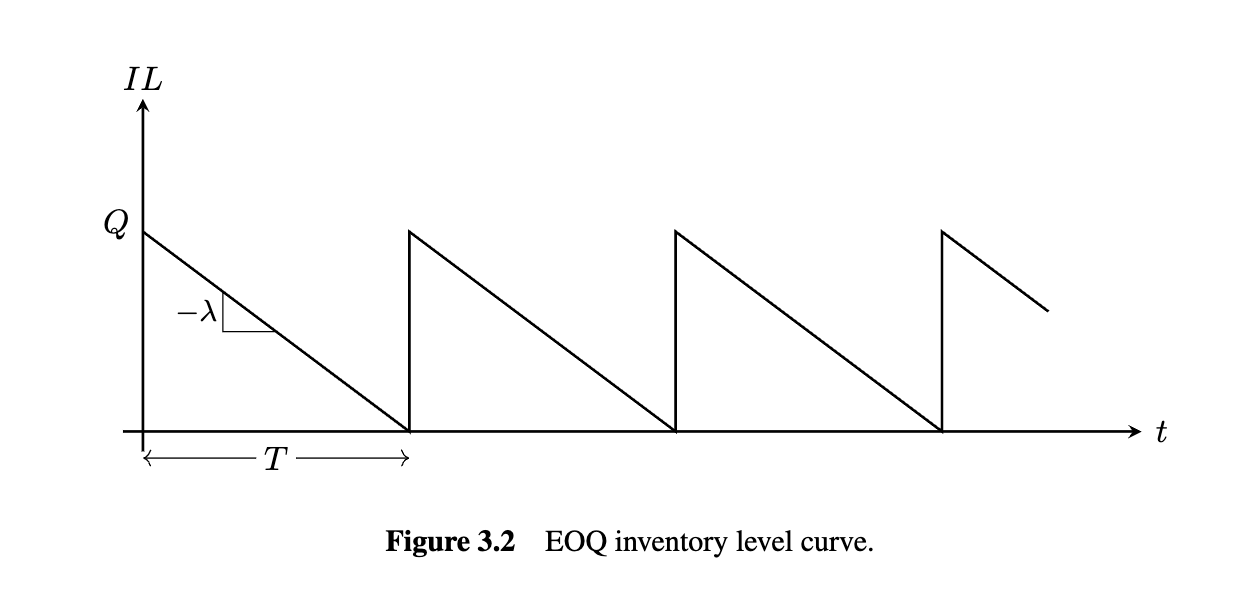
$T$ is the cycle length. meaning the amount of time between orders, and it relates to the order quantity $Q$ and $\lambda$ by the equation: \[ T = \frac{Q}{\lambda} \]

3.2.2 Cost Function

We want to find the optimal Q to minimize the average annual cost.

he key trade-off is between fixed cost and holdingcost: If we use a large $Q$, we’ll place fewer orders and hold more inventory (small fixedcost but large holding cost), whereas if we use a small $Q$, we’ll place more orders and holdless inventory (large fixed cost but small holding cost). - Order cost per year \[ \frac{K}{T} = \frac{K\lambda}{Q} \] - Average Annual Holding Cost \[ \frac{hQ}{2} \] where $K$ is a fixed cost per order, $h$ is an inventory holding cost per unit per year. $c$ is purchase cost per unit ordered.

The average inventory level in a cycle is $Q/2$, so the average amount ofinventory per year is $Q/2$ ·1 year = $Q/2$ - Total Cost \[ g(Q) = \frac{K\lambda}{Q} + \frac{hQ}{2} \]

3.2.3 Optimal Solution

The optimal $Q$ can be obtained by taking the derivative of $g(Q)$ and setting it to $0$:

\[ \begin{aligned} \frac{d g(Q)}{d Q}=-\frac{K \lambda}{Q^2}+\frac{h}{2} & =0 \\ \Longrightarrow Q^2 & =\frac{2 K \lambda}{h} \\ \Longrightarrow Q^* & =\sqrt{\frac{2 K \lambda}{h}} \end{aligned} \]

$Q^*$ is the economic order quantity. Then, the optimal total cost is $g(Q^*)$ is: \[ g(Q^*) = \sqrt{2K\lambda h} \] Another way to see that the fixed and holding costs are equal in the optimal solution isto note that the product of the two terms in (3.3) i

The ability to express g(Q∗) in closed form allows us to learn about structuralproperties of the EOQ and related models, such as the power-of-two policies discussed inSection 3.3, as well as to embed the EOQ into other, richer models, such as the locationmodel with risk pooling (LMRP) in Section 12.2

make some statements about how the solution changes asthe parameters change:

Remember that the EOQ only reflects costs, not revenues; the increased cost of large λwould be outweighed by the increased revenue

3.2.4 Sensitivity Analysis

Suppose the firm did not want to order $Q^∗$ exactly. For example, it might need to order in multiples of $10 (Q = 10n)$, or it might want to order every month ($T = 1/12$). Theorem: Suppose $Q^*$ is the optimal order quantity in the EOQ model, then for any $Q>0$: \[ \frac{g(Q)}{g(Q^*)} = \frac{1}{2} \left( \frac{Q^*}{Q} + \frac{Q}{Q^*}\right) \]

Theorem 3.2 ignores the per-unit cost c. If we include the annual cost cλin the numeratorand denominator of (3.8), then the percentage increase in cost would be even smaller

3.2.5 Order Lead Times

What if the lead time was positive—say, L years? Theoptimal solution doesn’t change—we just place our order L years before it’s needed.

It’s generally more convenient to express this in terms ofthe reorder point ($r$). So how do we compute $r$? It should be equal to the amount of product demanded during the lead time, or \[ r = \lambda L \]

3.3 Power-of-two Policies

In this section, we discusspower-of-two policies, in which the order interval is required to be a power-of-two multipleof some base period.

hen the power-of-two restriction says that orders can beplaced every 1 day, or every 2 days, or every 4 days, or every 8 days, and so on

Wealready know that the EOQ model is relatively insensitive to deviations from the optimalsolution from Theorem 3.2. Our goal is to determine exactly how much more expensive apower-of-two policy is than the optimal policy

he problem of finding optimalorder intervals in this setting is one version of a problem known as the one warehouse,multiretailer (OWMR) problem

3.3.2 Error Bound

Theorem 3.3

Theorem 3.3 If $\hat T$ is the optimal power-of-two order interval and $T^∗$ is the optimal (not necessarily power-of-two) order interval, then \[ \frac{f(\hat T)}{f(T^*)} \le \frac{3}{2\sqrt2} \approx 1.06 \] n other words, the cost of the optimal power-of-two policy is no more than 6% greaterthan the cost of the optimal (non-power-of-two) policy Hints for proof: the optimal power-of-two order interval $\hat T$ must be in the interval $\left[ \frac{1}{\sqrt 2} T^*, \sqrt 2 T^* \right]$. Since we don't know precisely where $\hat T$ falls in the range, so it is only a worst-case bound that occurs on the endpoints of the range.

3.4 The EOQ With Quantity Discounts

It is common for suppliers to offer discounts based on the quantity ordered

The specificstructure for the discounts can take many forms, but two types are most common: all-unitsdiscounts and incremental discount

3.4.1 All-Units Discounts

We can no longer ignore the purchase cost as we did in (3.3). In fact, not only do we needto include the purchase cost itself, but we must also account for the fact that the holdingcost typically depends on the purchase cost

Suppose we knew that the optimal order quantity lies in region $j$. Then we would simplyneed to find the $Q$ that minimizes the EOQ cost function for region $j$: \[ g_j(Q) = c_j \lambda + \frac{K\lambda}{Q} + \frac{ic_jQ}{2} \] Its minimizer is given by: \[ Q_j^* = \sqrt{ \frac{2K\lambda}{ic_j}} \]

3.4.2 Incremental Discounts

We now turn our attention to incremental discounts. The total cost function for region $j$ is given by \[ g_j(Q) = \frac{c(Q)}{Q} \lambda + \frac{K\lambda}{Q} + \frac{i \frac{c(Q)}{Q}Q}{2} \] where \[ c(Q) = \sum\limits_{i=0}^{j} c_i (b_{i+1} - b_i) + c_j (Q -b_j) \] Then, we can rewrite $g_j(Q)$ as \[ \begin{aligned} g_j(Q)= & \frac{1}{Q}\left[\sum_{i=0}^{j-1} c_i\left(b_{i+1}-b_i\right)-c_j b_j\right] \lambda+c_j \lambda+\frac{K \lambda}{Q} \\ & +\frac{i}{2}\left[\sum_{i=0}^{j-1} c_i\left(b_{i+1}-b_i\right)-c_j b_j\right]+\frac{i c_j Q}{2} \\ = & c_j \lambda+\frac{i \bar{c}_j}{2}+\frac{\left(K+\bar{c}_j\right) \lambda}{Q}+\frac{i c_j Q}{2} \end{aligned} \] where \[ \bar c_j = \sum_{i=0}^{j-1} c_i\left(b_{i+1}-b_i\right)-c_j b_j \] so the minimizer is given by \[ Q^* = \sqrt{ \frac{2(K + \bar c_j)\lambda}{i c_j}} \] with cost \[ g_j(Q^*) = c_j \lambda + \frac{i \bar c_j}{2} + \sqrt{ 2(K + \bar c_j)\lambda i c_j} \]

3.4.3 Modified All-Units Discounts

All-units discounts are somewhat problematic because, for order quantities Q just to theleft of breakpoint j, it is cheaper to order bj than to order Q

This structure is sometimes known as the modified all-units discount structure.

A special case of the modified all-units discount structure is the carload discount struc-ture, in which the bj are equally spaced and cj is the same for all j.

Unfortunately, modified all-units discount structures are much more difficult to analyzethan the discount structures discussed above.

3.5 The EOQ with Planned Backorders

In this section, we discuss avariant of the EOQ problem in which backorders are allowed. Let $p$ be the backorder penalty per item per year, and let $x$ be the fraction of demand that is backordered. Both $Q$ and $x$ are decision variables. The holding cost is charged based on on-hand inventory; the average on-hand inventory is given by: \[ \frac{1}{2} Q(1-x) \cdot\frac{(1-x)T}{T} = \frac{Q(1-x)^2}{2} \] Similarly, the average backorder level is: \[ \frac{Qx^2}{2} \] There, the total average cost per year in the EOQB is given by: \[ g(Q,x) = \frac{hQ(1-x)^2}{2} + \frac{pQx^2}{2} + \frac{K\lambda}{Q} \] Therefore, to minimize it, we need to take partialderivatives with respect to both variables and set them equal to 0. \[ \begin{align} \frac{\partial g}{\partial x} &=-h Q(1-x)+p Q x=0 \\ \frac{\partial g}{\partial Q} &=\frac{h(1-x)^2}{2}+\frac{p x^2}{2}-\frac{K \lambda}{Q^2}=0 \end{align} \] for the first equation, we have: \[ \begin{aligned} -h Q(1-x)+p Q x & =0 \\ \Longleftrightarrow h(1-x) & =p x \\ \Longleftrightarrow x^* & =\frac{h}{h+p} \end{aligned} \] Then, plug $x^*$, we have \[ \begin{align*} Q^* &= \sqrt{\frac{2K\lambda}{h(1-x)^2 + px^2}} \\ Q^* &= \sqrt{\frac{2K\lambda (p+h)}{hp}} \end{align*} \] Then \[ g(Q^*, x^*) = \sqrt{\frac{2K\lambda hp}{h+p}} \] How do the optimal solution and cost in Theorem 3.5 compare to the analogous quantitiesfrom the EOQ model? As $p\to \infty$, $Q^∗$ approaches the optimal EOQ order quantity, $x^∗$ approaches 0, and the optimal cost approaches the EOQ optimal cost.

As we continue to increase the number of backorders, the marginal savingsin holding cost decreases and the marginal increase in backorder cost increases

3.6 The Economic Production Quantity Model

In a manufacturing environment, the amount of time required to produce a batch of itemsusually depends on how large the batch is—producing more items requires more time.

n other words,the EOQ assumes that the production rate is infinite—an arbitrary number of items can beproduced in a fixed amount of time

Let ρ = λ/μ be the utilization ratio, which indicates the portion of time the system isactive. Q is now interpreted as a production batch size rather than an order quantity.

The fixed cost per year is still Kλ/Q, as in the EOQ model, since T = Q/λ.

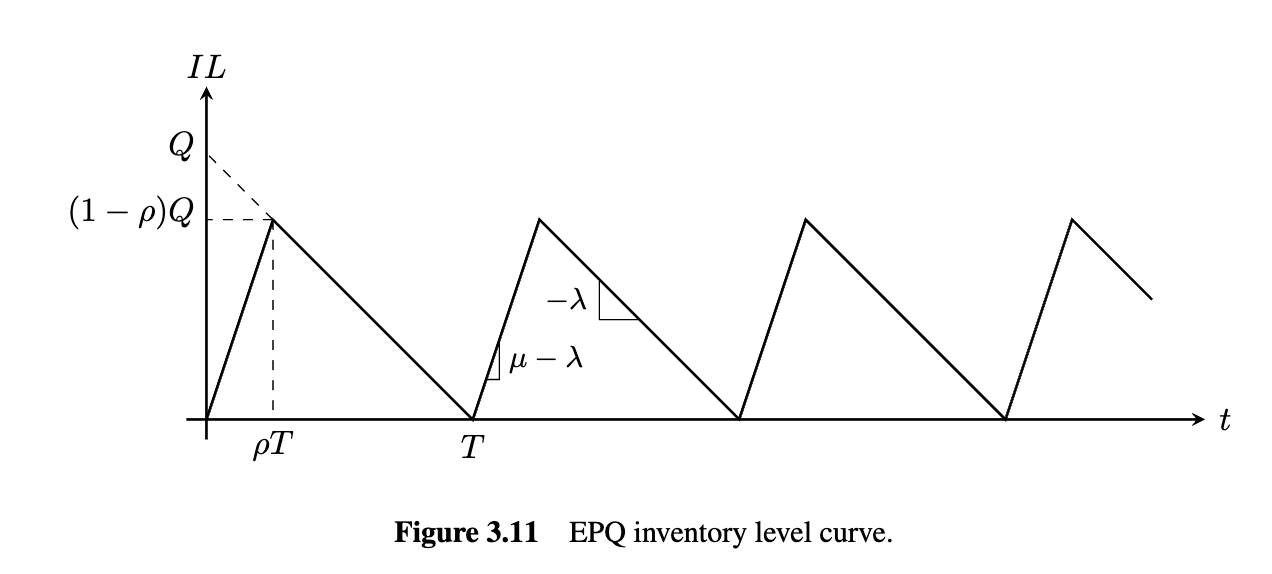
The order interval \[ T = \frac{Q}{\lambda} \]
Active interval \[ \frac{Q}{\mu} = \rho T \]
Maximum inventory level \[ \rho T (\mu - \lambda) = (1-\rho) Q \]
Fixed cost per year: $\frac{K \lambda}{Q}$
Average inventory level: $\frac{(1-\rho)Q}{2}$
Average annual holding cost: $\frac{h(1-\rho)Q}{2}$
Total annual cost \[ g(Q) = \frac{K\lambda}{Q} + \frac{h(1-\rho)Q}{2} \] We could find the Q that minimizes this cost function by differentiating, as we did for theEOQ,

3.7 Periodic Review: The Wagner-Whitin Model

3.7.1 Problem Statement

We now shift our attention to a periodic-review model known as the Wagner–Whitinmodel

he Wagner–Whitin modelassumes that the demand is deterministic, there is a fixed cost to place an order, and stock-outs are not allowed

However, unlike the EOQ model, the Wagner–Whitin model allows the demand to changeover time—to be different in each period

his model is sometimes referred to as thedynamic economic lot-sizing (DEL) model or the uncapacitated lot-sizing (ULS) model.

We first formulate this model as a mixed-integer optimization problem (MIP). We willthen discuss a dynamic programming (DP) algorithm for solving it.

3.7.2 MIP Formulation

Constraints (3.34)are the inventory-balance constraints: They say that the ending inventory in period t isequal to the starting inventory, plus the new units ordered, minus the demand.

This problem can be interpreted as a simple supply chain network design problem

It can be solved as an MIP, but it ismore common to solve it using DP or as a shortest path problem, as we discuss in the nextsection

3.7.3 Dynamic Programming Algorithm

Theorem 3.7 Every optimal solution to the Wagner–Whitin model has the ZIO property;that is, it is optimal to place orders only in time periods in which the initial inventory iszero

Despite the efficiency of this algorithm, a number of heuristicshave been introduced and are still popular in practice. These include Silver–Meal, partperiod balancing, least unit cost, and other heuristics

4. Stochastic Inventory Models: Periodic Review

In this chapter and the next, we will consider inventory models in which the demand isstochastic

A key concept in these chapters will be that of a policy. A policy is a simple rulethat provides a solution to the inventory problem.

One could imagine severalpossible policies for this system. Here are a few: 1. Every $R$ periods, place an order for $Q$ units.
2. Whenever the inventory position falls to $s$, order $Q$ units.
3. Whenever the inventory position falls to $s$, place an order of sufficient size to bring the inventory position to $S$. 4. Place an order whose size is equal to the first two digits of last night’s lottery number. Then, wait a number of periods equal to the last two digits of the lottery number before placing another order.

Forexample, policy 1 sounds reasonable, but only if we choose good values for R and Q. When using policies, then, inventory optimization really has two parts: Choosing theform of the optimal policy and choosing the optimal parameters for that policy.

Similarly, for some problems,no one even knows the form of the optimal policy, so we simply choose a policy that seemsplausible

Before continuing, we introduce two important concepts in stochastic inventory theory:cycle stock and safety stock. - Cycle stock (or working inventory) is the inventory that is intended to meet the expected demand. - Safety stock is extra inventory that’s kept on hand to buffer against uncertainty.

We’ll see later that the cycle stock depends on the mean of the demand distribution, whilethe safety stock depends on the standard deviation.

4.2 Demand Processes

In real life, customers tend to arrive at a retailer at random, discrete points in time.

One way to model these demands is using a Poisson process, which describesrandom arrivals to a system over time.

Sometimes, the normal distribution is used as an approximationfor the Poisson distribution, in which case $μ = σ^2$ since the Poisson variance equals itsmean. (This approximation is especially accurate when the mean is large.

One drawback to using the normal distribution is that any normal random variable willsometimes have negative realizations, even though the demands that we aim to model arenonnegative

This suggeststhat the normal distribution is appropriate as a model for the demand only if $μ \gg σ$ — say,if $μ > 4σ$.

4.3 Periodic Review With Zero Fixed Costs: Base-stock Policies

For the remainder of this chapter, we focus on periodic-review models

We will model the time value of money by discounting future periods using a discountfactor $\gamma \in (0,1]$

For the single-period and finite-horizonproblems, our objective will be to minimize the total expected discounted cost over thehorizon

4.3.1 Base-Stock Policies

A base-stock policy works as follows: In each time period, we observe the current inventory position and then place an order whose size is sufficient to bring the inventory position up to $S$

4.3.2 Single Period: The Newsvendor Problem

Single-period models are most often applied to perishable products, whichinclude (as you might expect) products such as eggs and flowers that may spoil, but alsoproducts that lose their value after a certain date,

This model is one of the most fundamental stochastic inventory models, and many ofthe models discussed subsequently in this book use it as a starting point.

If the newsvendor has unsold newspapers left at the endof the day, he cannot sell them the next day, but he can sell them back to the publisherfor $0.12 (called the salvage value).

The inventory carried by the newsvendor can be decomposed into two components:cycle stock and safety stock

As previously noted, the newsvendor model applies to perishable goods. In particular,it applies to goods that perish before the next ordering opportunity.

The holding cost is the cost per unitof positive ending inventory, while the stockout cost is the cost per unit of negative endinginventory. The costs h and p are sometimes referred to as overage and underage costs,

We will refer to the model discussed here as the implicit formulation of the newsvendorproblem since the costs and revenues are not modeled explicitly but instead are accountedfor in the holding and stockout costs $h$ and $p$

Our goal is to determine the base-stock level $S$ to minimize the expected cost in thesingle period.

These functions are known as the loss function and the complementary loss function,3respectively. Let $I(S,d) = (S-d)^+$, and $B(S, d) = (d-S)^-$ be the on-hand inventory and backorders, respectively. At the end of period if the firm orders up to $S$ and sees a demand of $d$ units. The cost for an observed demand od $d$ is: \[ \begin{align} g(S, d) &= h I(S,d) + pB(S,d) \\ & =h(S-d)^+ + p(d-S)^- \end{align} \] Since the demand is stochastic, however, we must have an expectation over $D$. Let $I(S) = \mathbb{E}[I(S,d)] = \mathbb{E}[B(S,D)]$ be the expected on-hand inventory and backorders if the firm orders up to $S$. Then \[ \begin{aligned} g(S) & =h I(S)+p B(S) \\ & =h \mathbb{E}\left[(S-D)^{+}\right]+p \mathbb{E}\left[(D-S)^{+}\right] \\ & =h \int_0^{\infty}(S-d)^{+} f(d) \operatorname d d+p \int_0^{\infty}(d-S)^{+} f(d) \operatorname d d \\ & =h \int_0^S(S-d) f(d) \operatorname d d+p \int_S^{\infty}(d-S) f(d)\operatorname d d \end{aligned} \] let \[ \begin{aligned} n(x) &=\mathbb{E}\left[(X-x)^{+}\right]=\int_x^{\infty}(y-x) f(y) \operatorname d y \\ \bar{n}(x) &=\mathbb{E}\left[(X-x)^{-}\right]=\int_0^x(x-y) f(y) \operatorname d y \end{aligned} \] Then: \[ g(S) = h \bar{n}(S)+pn(S) \] Since \[ \begin{align} \bar{n}(S) &=\int_0^S(S-d) f(d)\operatorname d d \\ &= \int_0^{+\infty}(S-d) f(d)\operatorname d d - \int_S^{+\infty}(S-d) f(d)\operatorname d d \\ &= S - \mu + \int_S^{+\infty}(d - S) f(d)\operatorname d d \\ &= S-\mu + n(S) \end{align} \] where $\mu$ is the mean value of $f(x)$. So we can simplify the expression of $g(S)$: \[ \begin{align} g(S) &= h [S-\mu +n(S)] +pn(S) \\ & = h(S-\mu) + (h+p) n(S) \end{align} \] These functions are known as the loss function and the complementary loss function, respectively. Here we can calculate the derivatives of the above two equations according to the Leibniz's Rule: \[ \begin{align} n^\prime(x) &= (y-x)f(y) \bigg|_{y=x} + \int_x^{+\infty} \frac{\partial(y-x)f(y)}{\partial x} \operatorname dy \\ \\ & = 0+ \int_x^{+\infty} (-1)f(y)\operatorname dy \\ \\ &= F(x) - F(+\infty) \\ \\ &=F(x) - 1 \end{align} \] Similarly, \[ \bar{n} ^\prime(x) = F(x) \] So we have $n^{\prime \prime} = \bar n^{\prime \prime} = f(x)>0$, so both $n(\cdot)$ and $\bar n(\cdot)$ are convex. To minimize $g(S)$, thus, we set its first derivative to $0$, $$ \[\begin{align} \frac{\operatorname dg(S)}{\operatorname d S} &= h + (h+p)[F(x)-1]=(h+p)F(S) - p = 0 \\ F(S) &= \frac{p}{h+p} \\ S & = F^{-1}\left(\frac{p}{p+h}\right) \end{align}\] $$

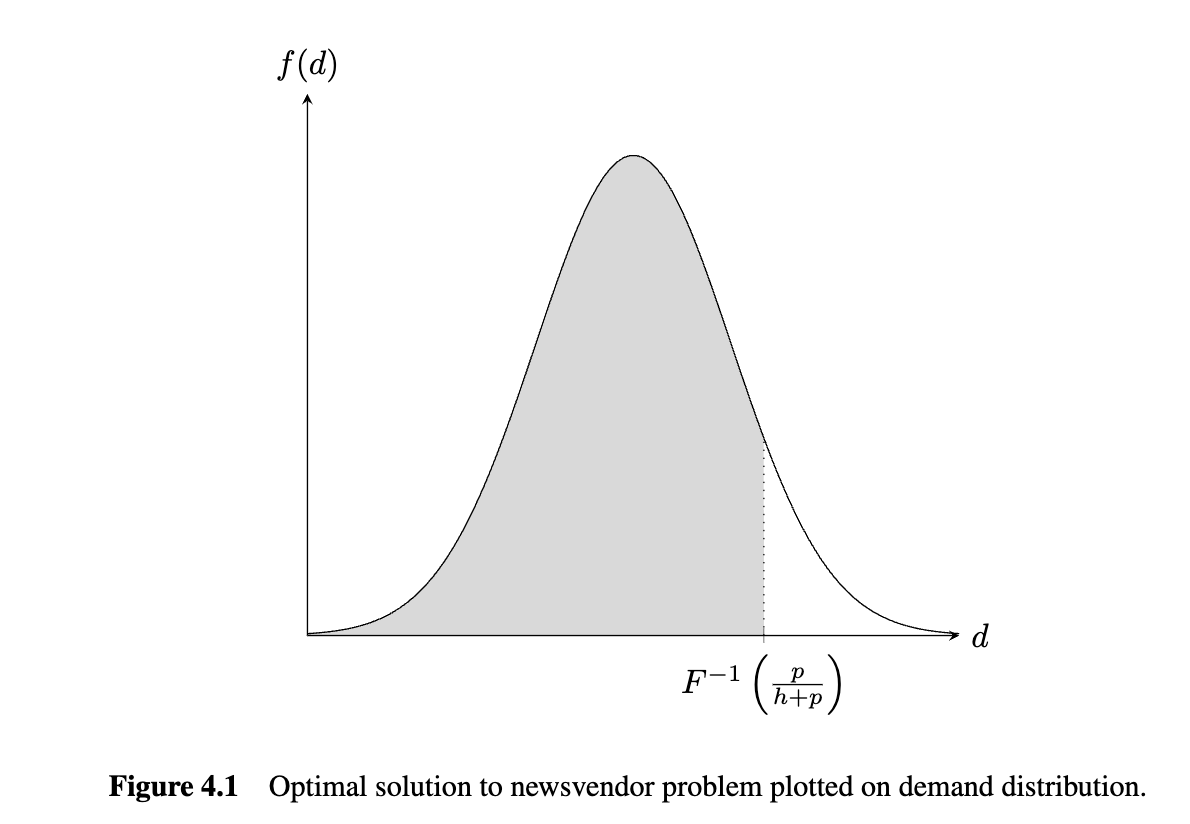
Note：直观来理解，就是最优解 $S^*$ 符合 $P[d>S^*] = \frac{p}{h+p}$, 即右边表示售罄是的损失 $p$, 左边表示持货成本 $h$。$S^*$ 会随着 $h$ 增加而减少，随着 $p$ 增加而增加。

Theorem 4.1 The optimal base-stock level for a single-period model with no fixed costs(the newsvendor model) is given by

p/(h + p) is known as the critical ratio (or critical fractile).

The formulation given in Sections 4.3.2.2–4.3.2.3 in-terprets hand pas the overage and underage costs, respectively—the cost per unit of havingtoo much or too little inventory.

Sometimes, this is instead formulated as a profit maximization problem in which we maximize $\pi(S) ≡−g(S)$.

We can translate this to the implicit version of the problem by determining the overageand underage costs Actually, we can translate this explicit formulation to the implicit version by determining the overage and underage costs (which we'll denote by $h^\prime$ and $p^\prime$, respectively). - $h^\prime = h+c-v$ : For each unit of excess inventory, we incur a holding cost of $h$, and we paid $c$ for the extra unit but earn $v$ as a salvage value. - $p^\prime = p+r-c$ : For each stockout, we incur a penalty of $p$ in addition to the lost profit $r-c$. \[ S^* = F^{-1} \left(\frac{p^\prime}{h^\prime+p^\prime}\right) = F^{-1} \left(\frac{p+r-c}{h+c-v+p+r-c}\right)= F^{-1} \left(\frac{p+r-c}{h+p+r-v}\right) \] where $r$ is the revenue earned per unit sold, $c$ is the cost per unit purchased, and $v$ is the salvage value earned for each unit of excess inventory.

t is perfectly acceptable to set any of the cost or revenue parameters to 0 if they arenegligible or should not be included in the model

If we let α = p/(h + p), we have If we let $\alpha= \frac{p}{h+p}$, we have \[ S^* = \mu + z_\alpha \sigma \] But should the firm order any units? By the convexity of g(S),the answer is no: It would be better to leave the inventory level where it is

one of the simplest is to use a moving average(Section 2.2.1) to estimate μand what we might call a moving standard deviation to estimateσ in period t

4.3.2.8 Discrete Demand Distributions Suppose now that D is discrete. In thiscase, (4.3) becomes

4.3.3 Finite Horizon

Now consider a multiple-period problem consisting of a finite number of periods, T.Suppose we are at the beginning of period t Let $\theta_t(x)$ be the optimal expected cost in periods $t, t+1, \cdots, T$ if we begin period $t$ with an inventory level $x$. Then, we have \[ \theta_t(x) = \min_{y\ge x} \left\{ c(y-x) + g(y) + \gamma \mathbb E_D[\theta_{t+1} (y-D)]\right\} \] where \[ \begin{aligned} g(y) =h \int_0^y(y-d) f(d) \operatorname d d+p \int_y^{\infty}(d-y) f(d)\operatorname d d = h\bar n(y) + p n(y) \end{aligned} \] The interpretation of each term can be explained as follows:

Note: figure from 【供应链理论基础】零固定成本的周期性盘点条件下基本库存策略（Base-Stock Policy）最优性的证明

First consider what happens at the end of the time horizon. Presumably, on-handunits and backorders must be treated differently now that the horizon has ended than theywould be during the horizon

4.3.4 Infinite Horizon

This problem is sometimes referred to as the infinite-horizon newsvendormodel.

An alternate objective is to minimizethe expected cost per period. The former case is known as the discounted-cost criterion,while the latter is known as the average-cost criterion Under the average cost criterion, we assume $\gamma = 1$. The expected cost in a given period if we use back-stock level $S$ is given by: \[ \begin{aligned} g(S) =h \int_0^S(S-d) f(d) \operatorname d d+p \int_S^{\infty}(d-S) f(d)\operatorname d d = h\bar n(y) + p n(y) \end{aligned} \] Now suppose $\gamma < 1$, consider the discounted-cost criterion. The optimal base-stock level is the same in every period, and it is given by \[ S^* = F^{-1} \left( \frac{p-(1-\gamma)c}{h+p}\right) \] Then, if demand is normally distributed, then after modifying to account for $\gamma$, the results would be \[ S^* = \mu + \sigma \Phi^{-1}\left( \frac{p-(1-\gamma)c}{h+p}\right) = \mu + z_\alpha \sigma \] where $\alpha = \left( \frac{p-(1-\gamma)c}{h+p}\right)$.

In formulating (4.38), we glossed over two potentially problematic issues. Two problematic issues: 1. Why didn’t we account for the purchase cost $c$, 2. Why didn’t we account for the cost in future periods?

4.4 Periodic Review With Nonzero Fixed Costs: $(s, S)$ Polices

4.4.1 $(s,S)$ Policies

We now consider the more general case in which the fixed cost K may be nonzero. If $K \neq 0$, it may no longer make sense to order in every period, since each order incurs a cost.

Instead, the firm should order only when the inventory position becomes sufficiently low.

Both $s$ and $S$ are constants, and $s ≤ S$.The quantity $s$ is known as the reorder point and $S$ as the order-up-to level

the optimality of (s,S) policies for multiperiod problems was not provenuntil Scarf’s (1960) paper

We will discuss how to determine the optimal s and S for the single-period, finite-horizon, and infinite-horizon cases separately

Actually, the single-period case is not nearly as useful for the $K > 0$ caseas it is for the $K = 0$ case

4.4.2 Single Period

For given $s$ and $S$, theordering rule is: If $x ≤ s$, order $S −x$; otherwise, order 0. 一旦订购（或不订购），就会产生持有和缺货成本，就像在零固定成本模型中一样，只是基础库存水平被 $S$（如果我们订购）和 $x$（如果我们不订购）取代。因此，该期间的总预期成本（作为 $s$ 和 $S$ 的函数）由下式给出 \[ g(s, S) = \left\{\begin{array}{l} K + g(S), &\text{if } x\leq s \\ g(x), & \text{if } x> s \end{array}\right. \]

Optimizing $g(s,S)$ over s and $S$ is actually quite easy (Karlin 1958b): We already knowfrom Theorem 4.1 that $F−1(p/(h + p))$ minimizes $g(S)$,

4.4.3 Finite horizon

The finite-horizon model with nonzero fixed costs can be solved using a straightforwardmodification of the DP model for the zero-fixed-cost case from Section 4.3.3.

Now $θ_t(x)$ must account for the fixed cost in period $t$ (if any), as well as the purchase cost and expected holding and stockout costs in period $t$, and the expected future costs, as in the $K = 0$ model. In particular Now $θ_t(x)$ must account for the fixed cost in period $t$ (if any), as well as the purchase cost and expected holding and stockout costs in period $t$, and the expected future costs, as in the $K = 0$ model. In particular, \[ \theta_t(x) = \min_{y \ge x}\left\{ K\delta (y-x) + c(y-x) + g(y) + \gamma \mathbb E_D[\theta_{t+1} (y-D)]\right\} \] where \[ \delta(z) = \left\{\begin{array}{l} 1, &\text{if } z>0 \\ 0, & \text{otherwise} \end{array}\right. \] Note : Since here fixed cost is not zero, so add the fixed costs term $K\delta (y-x)$. It also consists of the general equation of periodic review, as follows (figure from Link):

However, just as before, we would rather have a simple policy to follow, rather than having to specify $y_t(x)$ for every $t$ and $x$

In particular, for period $t$, there are values $S_t$ and $s_t$ such that for $x \leq s_t$, we have $y_t(x) = S_t$, and for $x > s_t$, we have $y_t(x) = x$. In other words, these curves each depict an $(s,S)$ policy.

4.4.4 infinite Horizon

Recall that the infinite-horizon model with no fixed costs (Section 4.3.4) is as simple asthe single-period model (Section 4.3.2).

nfortunately, this is not true in the fixed-costcase. The infinite-horizon model is more difficult than its single-period or finite-horizoncounterparts

A renewal process is a random variable $N(t)$ that counts the number of “renewals”that have occurred by time $t$, where the amount of time between the $(n −1)st$ renewal and the nth renewals is a random variable $X_n$

4.5 Policy Optimility

Now that we know how to find the optimal $S$ for a base-stock policy (Section 4.3) and the optimal $s$ and $S$ for an $(s,S)$ policy (Section 4.4), we prove that those policy types are in fact optimal for their respective problems

e are trying toshow that no other policy, of any type, using any parameters, can outperform our chosenpolicy type (provided we choose the optimal parameters) in the long run

We will first consider the zero-fixed-cost case, then the fixed-cost case, in both casesconsidering single-period, finite-horizon, and infinite-horizon cases separately

We continue to assumethat the cost and demand parameters are stationary, but the results below still hold if thesevary from period to period (deterministically). Recall the optimal cost in periods $t, \cdots, T$ if we begin period $t$ with an inventory level of $x$, can be calculated recursively as: \[ \theta_t(x) = \min_{y \ge x}\left\{ K\delta (y-x) + c(y-x) + g(y) + \gamma \mathbb E_D[\theta_{t+1} (y-D)]\right\} \]

Our goal throughout this section will be to use the structure of (4.81) toshow that the optimal actions follow the policies we have conjectured are optimal

4.5.1 Zero Fixed Costs: Base-Stock Policies

We first consider the case in which K = 0 and prove that—regardless of the horizonlength—a base-stock policy is always optimal Single Period:

we’ll consider the special case in which $T = 1$ and $K = 0$. We’ll also assume that the terminal cost function (i.e., $\theta_{t+1} (x) = 0$, see Section 4.3.3) is equal to 0. Then, the optimal cost reduces to: \[ \theta(x) = \min_{y \ge x}\left\{c(y-x) + g(y) \right\} \] We cam rewrite $\theta(x)$ as \[ \theta(x) = \min_{y \ge x}\left\{H(y) -cx \right\} \] where \[ H(y) = cy + g(y) \] Since we are calculating $θ(x)$ for fixed $x$, we see that the optimal decision can be found by minimizing $H(y)$ over $y \ge x$, that is, starting at $y = x$, we want to minimize $H(y)$ looking only “to the right” of $x$.

If $H(y)$ is convex, we can have: - If $x < S$, then the optimal strategy is to set $y = S$ - if $x \ge S$, the optimal strategy is to do nothing, to set $y = x$. In other words, the optimal policy is a base-stock policy.

And H(y) is convex because g(y) is convex,so we have now sketched the proof of the following theorem.

Theorem 4.10 A base-stock policy is optimal for the single-period problem with no fixedcosts. Finite Horizon:

It was simple to prove that H(y) is convex, and therefore thata base-stock policy is optimal, for the single-period problem

4.5.2 Nonzero Fixed Costs: $(s, S)$ Policies

We now allow K 6= 0 and prove that an (s,S) policy is optimal.

4.6 Lost Salse

Throughout this chapter, we have assumed that unmet demands are backordered.

we assume instead that they are lost. The distinction is only important when T > 1.(When T = 1, unmet demands can only be lost.)

4.6.1 Zero Lead Time

First consider the case in whichK = 0. In the finite-horizon model, the DP recursion (4.36) changes only slightly \[ \theta_t(x) = \min_{y \ge x}\left\{c(y-x) + g(y) + \gamma \mathbb E_D[\theta_{t+1} (y-D)]^+\right\} \] Note: the positive part of $y −D$ to reflect the fact that the inventory level cannot become negative.

A base-stock policy is still optimal for the infinite-horizon model. Under the average-cost criterion (γ = 1) with lost sales,

5. Stochastic Inventory Models: Continuous Review

5.1 $(r, Q)$ Policies

In this chapter, we consider a setting similar to the economic order quantity (EOQ) model(Section 3.2) but with stochastic demand.

The inventory position is monitored continuously, and orders may be placed at any time. There is a deterministic lead time $L (\ge0)$. Unmet demands are backordered

If the demand has a continuous distribution, then the inventory level decreases smoothlybut randomly over time, with rate $λ$,

$(r, Q)$ Policy:

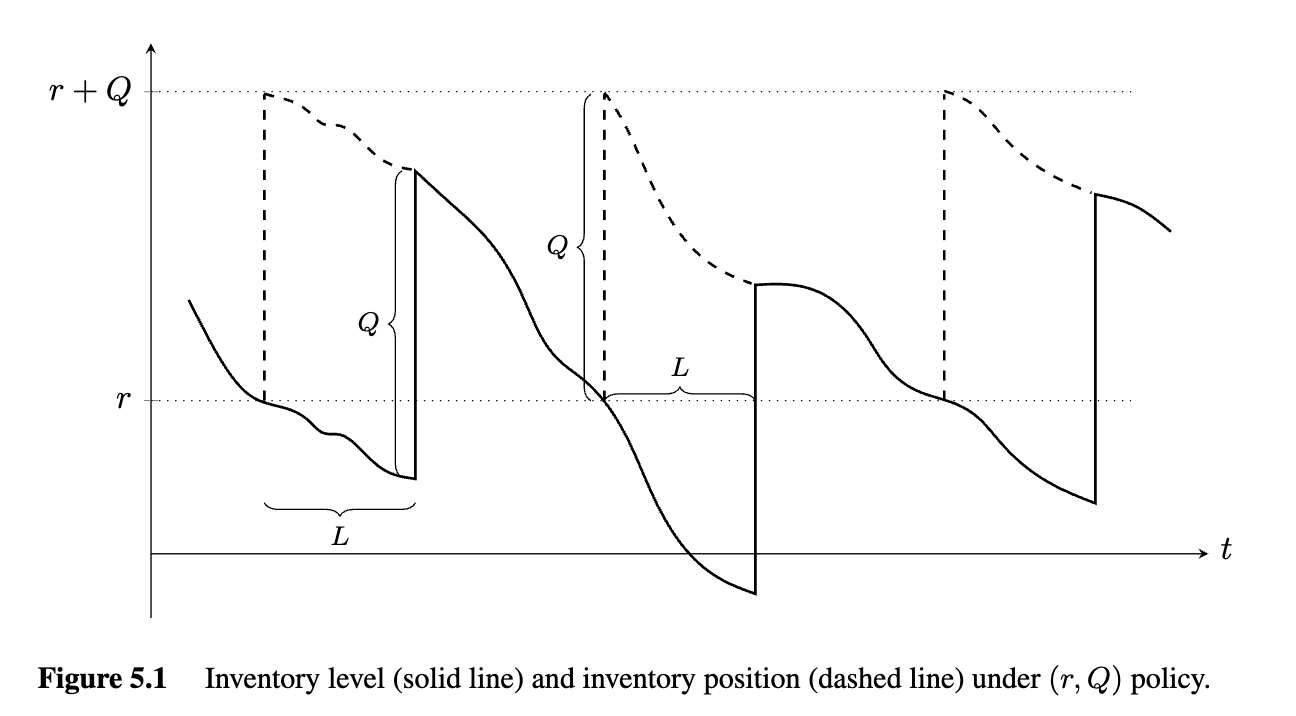
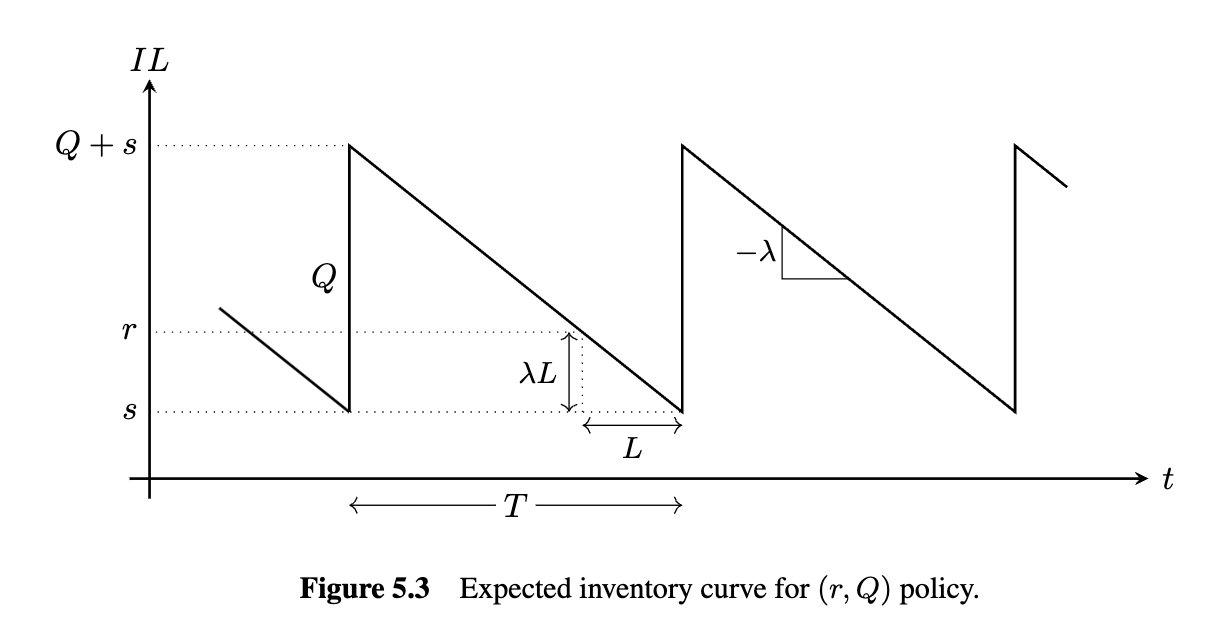
We’ll assume the firm follows an (r,Q) policy: When the inventory position reaches acertain point (call it r), we place an order of size Q. L years later, the order arrives

Note that the inventory level (solid line in Figure 5.1) and inventoryposition (dashed line) differ from each other during lead times but coincide otherwise. Differing from the EOQ model, which has a single decision variable $Q$, the $(r, Q)$ Policy has two decision variables: $Q$ (the order quantity, sometimes called the batch size) and $r$ (the reorder point)

Our goal is to determine the optimal r and Q to minimize the expected costper year.

since in either case theinventory position may fall strictly below the reorder point before a replenishment order isplaced.

5.2 Exact $(r, Q)$ Problem With Continuous Demand Distribution

we introduce an exact model for systems with continuous demand distribu-tions. We first formulate the expected cost function and then derive optimality conditionsfor it The usual costs: - Fixed cost: $K \ge 0$ - Purchase cost: $c \ge 0$ - Holding cost: $h > 0$ - Stockout cost: $p>0$ - $D$: the lead-time demand (运输期间的需求), a random variable with mean $\mu$ and variance $\sigma^2$, pdf $f(d)$ and cdf $F(d)$

5.2.1 Expected Cost Function

Our first step is to derive an exact expression for the expected cost as a function of r and Q. First, we place orders, on average every $Q/\lambda$ years. There the expected fixed cost is given by $K\lambda/Q$.

If the inventory position at time $t$ is given by $IP(t)$, then the inventory level at time $t +L$ is given by: \[ IL(t+L) = IP(t) - (t, t+L] \] As in the periodic-review case, we can drop the time indices in steady state and write: \[ IL = IP -D \] where $D$ is the lead-time demand.

Once we determine the distribution of IP, the (unconditional) expected inventory costthen follows from the law of total expectation. Let $\bar g(x)$ be the rate at which the inventory cost accrues when $IL = x$: \[ \bar g (x) = hx^+ + px^- \] Note: $g(\cdot)$ is a rate because the inventory level is changing continuously over time, given in units of money per year. Then the expected inventory cost per year is: \[ \begin{aligned} \mathbb{E}[\text { inventory cost }] & =\mathbb{E}_{I L}[\bar{g}(I L)] \\ & =\mathbb{E}_{I P}\left[\mathbb{E}_{I L \mid I P}[\bar{g}(I L)]\right] \\ & =\mathbb{E}_{I P}\left[\mathbb{E}_D[\bar{g}(I P-D)]\right] \\ & =\mathbb{E}_{I P}[g(I P)] \end{aligned} \] where \[ g(y) = h \mathbb{E}[(y-D)^+] + p \mathbb{E}[(D-y)^+] \] $g(y)$ is the rate at which the expected inventory cost accrues at time $t + L$ when the inventory position at time $t$ equals $y$.

It remains to determine the distribution of $IP$. By the definition of an $(r,Q)$ policy, we know that $IP$ takes values only in $[r,r + Q]$.

在一些简单例子中，$IP$ 可以是简单的分布，如均匀分布。因此，我们可以用如下积分形式计算 期望损失： \[ \mathbb {E} [\text{inventory cost}] = \frac{1}{Q} \int_r^{r+Q}g(y) \operatorname d y \] Combining the expected inventory cost and the expected fixed cost $K\lambda/Q$, we have the expected total cost per year: \[ g(r, Q) = \frac{K\lambda + \int_r^{r+Q}g(y) \operatorname d y}{Q} \] Lemma 5.1 g(r,Q) is jointly convex in r and Q.

In what follows, we use the expected cost expression (5.7) to derive optimality conditionsfor $r$ and $Q$ by first fixing $Q$ and finding the optimal corresponding $r$, and then optimizingover $Q$

5.2.2 Optimality Conditions

Lemma 5.2 For any $Q > 0, r = r(Q)$ if and only if Lemma For any $Q > 0, r = r(Q)$ if and only if \[ g(r) = g(r+Q) \] The motivation behind this result is that, during one replenishment cycle, we need topass through all of the inventory positions in [r,r + Q] Theorem $(r,Q)$ minimize $g(r,Q)$ if and only if: \[ g(r, Q) = g(r +Q) = g(r) \]

5.3 Approximations for $(r, Q)$ Problem With Continuous Distribution

5.3.1 Expected-Inventory-Level Approximation

The first approximation we discuss is probably the best known and most widely coveredapproximation to find r and Q.

We call this the expected-inventory-level (EIL) approximation,for reasons that will become clear shortly

The approach relies on the following two simplifying assumptions to make the modeltractable: Two assumptions: 1. Simplifying Assumption 1 (SA1): Incur holding costs at a rate of $h \cdot IL$ per year, where $IL$ is the inventory level, whether $IL$ is positive or negative. 2. Simplifying Assumption 2 (SA2): The stockout cost is charged once per unit of unmet demand, not per year.

The costs: - The expected on-hand inventory when the order arrives:

\[ s = r -\lambda L \]

The average inventory level:

\[ s+\frac{Q}{2} = r -\lambda L +\frac{Q}{2} \]

By SA1, the expected holding cost per year is: \[ h\left( r -\lambda L +\frac{Q}{2}\right) \] Note: this expression is only approximate, since that we are calculating the expected holding cost as $h \cdot \mathbb{E}[IL]^+$ (provided that $\mathbb{E}[IL]>0$).

That is why we refer to this as the “expected-inventory-level” approximation. The problem is more difficult without SA1 because of the nonlinearity introduced by the $[·]^+$ operator. 2. Fixed cost : $\frac{K\lambda}{Q}$ - Stockout cost :

\[ \mathbb{E}[(D-r)^+] = \int_r^\infty (d-r) f(d)\operatorname dd = n(r) \]

where $n(r)$ is the loss function for the lead-time demand distribution

The expected number of stockout per year is \[ \frac{n(r)}{\mathbb{E}[T]} = \frac{\lambda n(r)}{Q} \] 3. then by SA2, the expected stockout cost per year is simply: \[ \frac{p \lambda n(r)}{Q} \]

Note that we are assuming that r > 0, which is a reasonable assumption in practice The total cost per year: \[ g(r, Q) = h\left( r -\lambda L +\frac{Q}{2}\right) + \frac{K\lambda}{Q} + \frac{p \lambda n(r)}{Q} \] Solution: - For $Q$ :

$$
\begin{align}
\frac{\partial g}{\partial Q} =\frac{h}{2}-\frac{K \lambda}{Q^2}-\frac{p \lambda n(r)}{Q^2} & =0 \\
\Longleftrightarrow \quad \frac{1}{Q^2}[K \lambda+p \lambda n(r)]=\frac{h}{2} \\
\Longleftrightarrow\quad Q^2=\frac{2[K \lambda+p \lambda n(r)]}{h} \\
Q=\sqrt{\frac{2 \lambda[K+p n(r)]}{h}} \\

\end{align}
$$

For $r$ :

\[ \begin{align} \frac{\partial g}{\partial r}=h+\frac{p \lambda n^{\prime}(r)}{Q}=0 \\ \Longleftrightarrow \quad h+\frac{p \lambda(F(r)-1)}{Q}=0 \\ r=F^{-1}\left(1-\frac{Q h}{p \lambda}\right) \end{align} \]

Now we have two equations with two unknowns, but these equations cannot be solvedin closed form.

The approach given in Algorithm 5.1 first sets Q equal to the EOQ quantity,i.e., ignoring the demand randomness.

One major limitation of (r,Q) policies as formulated aboveis that p is very hard to estimate

5.3.2 EOQB Approximation

There are important connections between the EOQ problem with planned backorders

5.3.3 EOQ + SS Approximation

Another common approximation for r and Q is to convert the inventory-cost parametersinto a service level and then to use the approach described in Section 5.3.1.3 for type-1service level constraints

5.4 Exact $(r, Q)$ Problem With Continuous Distribution: Properties of Optimal $r$ and $Q$

We now return to the exact model from Section 5.2. We have two main goals in thissection 1. We will analyze the properties of optimal solutions (and their costs) for $(r, Q)$ policies, by deriving optimality conditions for $r$ and $Q$ and then providing properties of the resulting optimal solutions. 2. We will compare $(r,Q)$ policies to the EOQB model and prove.

if the EOQB model is used as a heuristic for optimizing r and Q, asdiscussed in Section 5.3.2, the resulting error has a fixed bound. Let $G(Q)$ equal the expected cost per year as a function of $Q$, assuming $r$ is set optimally for that $Q$, \[ G(Q) = g(r(Q), Q) \] Let $H(Q)$ be the value of $g(y)$ at $y=r(Q)$, or $r(Q)+Q$ \[ H(Q) = g(r(Q)) = g(r(Q)+Q) \] Then we have \[ G(Q) = \frac{K\lambda + \int_0^{Q}H(y) \operatorname d y}{Q} \]

6. Multi-echelon Inventory Models

we study inventory optimization models for multiechelon (or multistage)systems with shipments made among the stages

6.1 Introduction

There are two common ways to interpret the stages or nodes in the multiechelon system: 1. Stages represent locations in a supply chain network, and links among the stages represent physical shipments of goods. 2. Stages represent processes that the product must undergo during manufacturing, assembly, and/or distribution.

the stages in Figure 6.1(a)may represent the following physical locations: a supplier in China, a factory inCalifornia, a warehouse in Chicago, and a retailer in Detroit (respectively).

For example, the stages in Figure 6.1(a) may represent thefollowing processes: manufacturing, assembly, testing, and packaging. These fourfunctions may take place in four different locations or all within the same building

8. Facility Location Models

8.1 Introduction

One of the major strategic decisions faced by firms is the number and locations of factories,warehouses, retailers, or other physical facilities

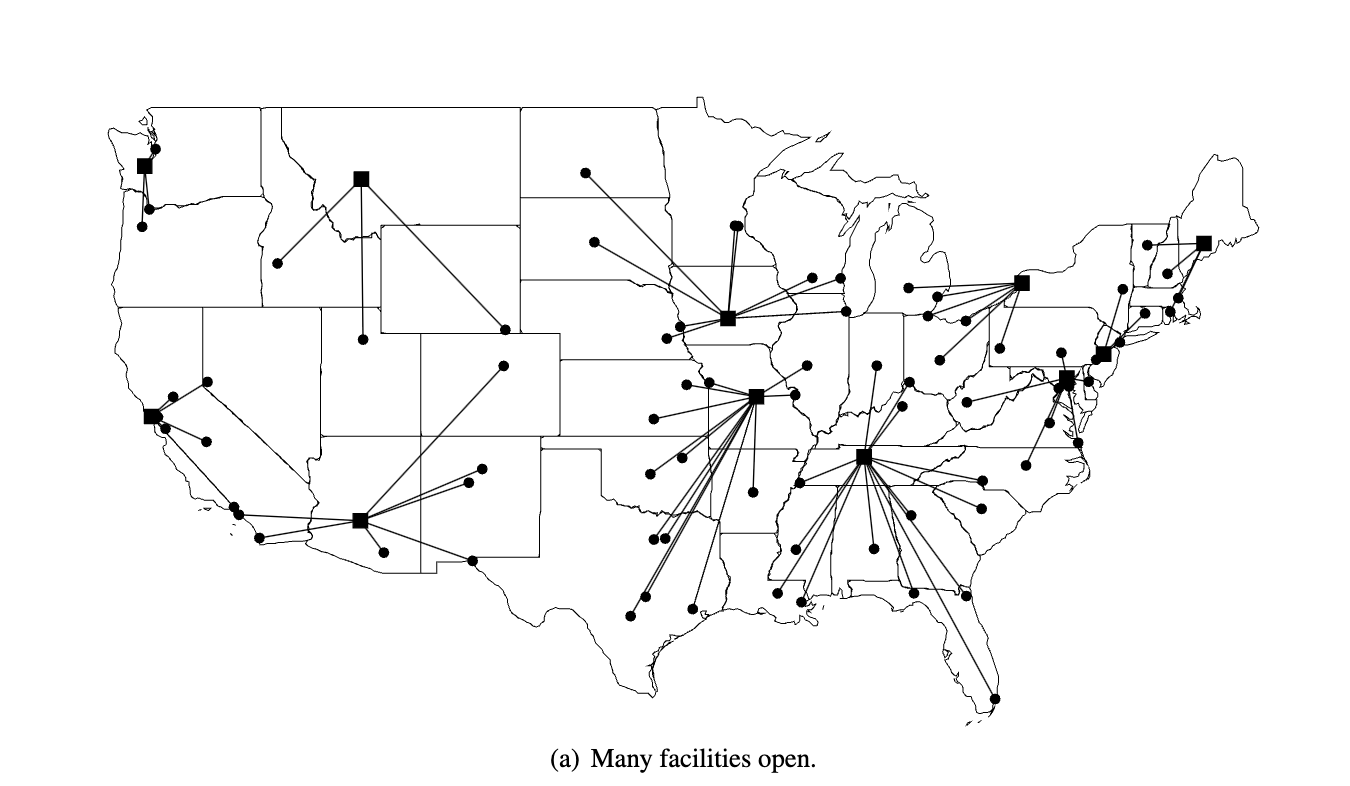
The key trade-off in most facility locationproblems is between the facility cost and customer service. - More facilities

If we open a lot of facilities(Figure 8.1(a)), we incur high facility costs (to build and maintain them), but we can providegood service since most customers are close to a facility.

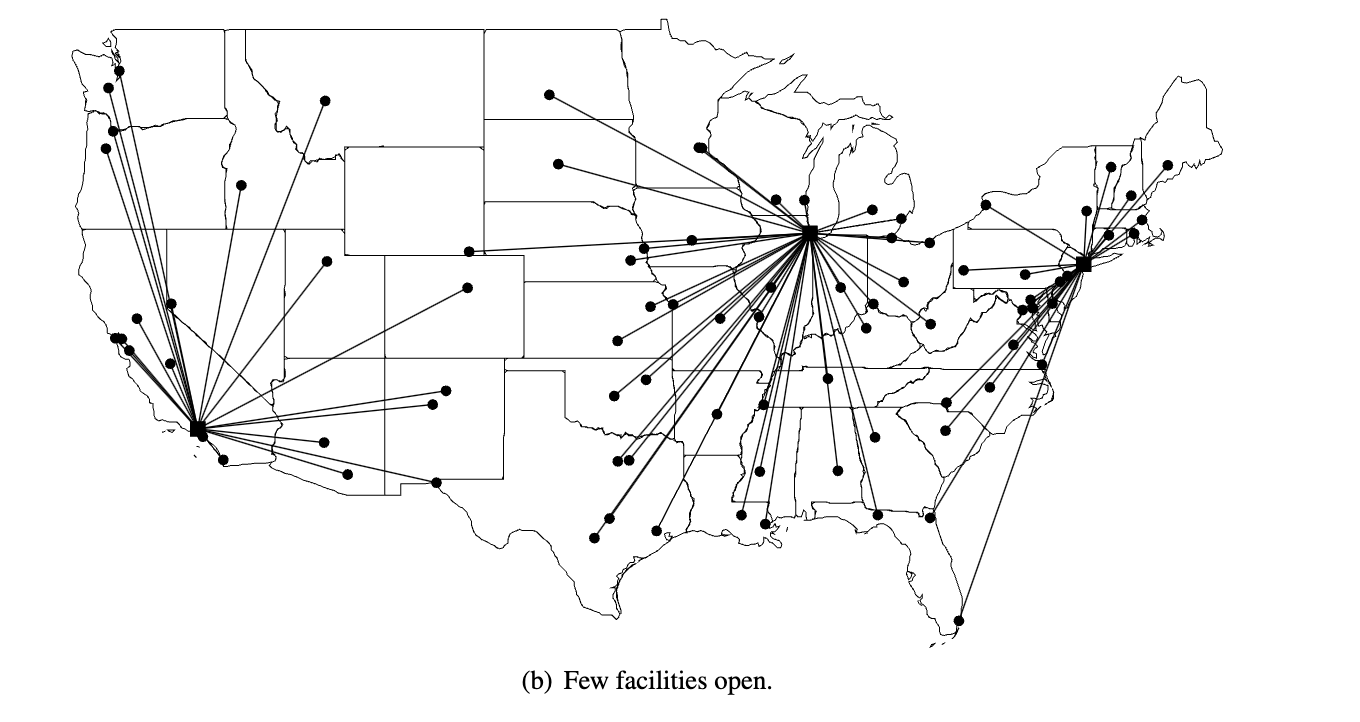
Few facilities

if we openfew facilities (Figure 8.1(b)), we reduce our facility costs but must travel farther to reachour customers (or they to reach us).

Most (but not all) location problems make two related sets of decisions: (1) where tolocate, and (2) which customers are assigned or allocated to which facilities.

Therefore,facility location problems are also sometimes known as location–allocation problems

These differ in terms of how they model facility costs (for example, some include the costsexplicitly, while others impose a constraint on the number of facilities to be opened) andhow they model customer service (for example, some include a transportation cost, whileothers require all or most facilities to be covered—that is, served by a facility that is withinsome specified distance).

In addition to supply chain facilities such as plants and warehouses, location modelshave been applied to public sector facilities

In addition, many operations research problems can be formulatedas facility location problems or have subproblems that resemble them

In this chapter, we will begin by discussing a classical facility location model, theuncapacitated fixed-charge location problem (UFLP)

we discuss cover-ing models (including the p-center, set covering, and maximal covering problems)

8.2 The Uncapacitated fixed-charge Location Problem

8.2.1 Problem Statement

The uncapacitated fixed-charge location problem (UFLP) chooses facility locations inorder to minimize the total cost of building the facilities and transporting goods fromfacilities to customers.

Sometimes it’s also useful to think of an upstream echelon,again with fixed location(s), that serves the DCs. - Fixed cost

Each potential DC location has a fixed cost that represents building (or leasing) thefacility; - Transportation cost

transportation cost per unit of product shipped from a DC to each customer. - Objective

The problem is to choosefacility locations to minimize the fixed cost of building facilities plus the transportationcost to transport product from DCs to customers, subject to constraints requiring everycustomer to be served by some open DC

As noted above, the key trade-off in the UFLP is between fixed and transportation costs

8.2.2 Formulation

Define the following notations:

Sets: - $I$ : set of customers - $J$: set of potential facility locations Parameters - $h_i$ : annual demand of customer $i \in I$ - $c_{ij}$ : cost to transport one unit of demand from facility $j \in J$ to customer $i \in I$ - $f_j$ : fixed annual cost to open a facility at site $j \in J$ Decision Variables - $x_j$ : 1 if facility $j$ is opened, 0 otherwise - $y_{ij}$ : the fraction of customer $i$'s demand that is served by facility $j$

Note : The transportation costs $c_{ij}$ might be of the form $k \times$ distance for some constant $k$ (if the shipping company charges k per mile per unit) or more arbitrary (for example, based on airline ticket prices, which are not linearly related to distance)

In the former case,distances may be computed in a number of ways: Distances: - Euclidean distance: - Manhattan or rectilinear metric - Great circle - Highway/network - Matrix

In general, we won’t be concerned with how transportation costs are computed—we’ll assume they are given to us already as the parameters $c_{ij}$ The UFLP is formulated as follows: \[ \min \quad \sum\limits_{j\in J} f_j x_j + \sum\limits_{i\in I} \sum\limits_{j\in J} h_i c_{ij} y_{ij} \] subject to \[ \begin{align} \sum\limits_{j \in J}y_{ij} &=1 &\forall i \in I \\ y_{ij} &\leq x_j &\forall i \in I, \forall j \in J \\ x_j &\in\{0, 1\} &\forall j \in J \\ y_{ij} &\ge 0 & \forall i \in I, \forall j \in J \end{align} \]

Note : in the discussion that follows, we’ll use $z^∗$ to denote the optimal objective value of (UFLP).

The objective function (8.3) computes the total (fixed plus transportation) cost.

In fact, it is always optimalto assign each customer solely to its nearest open facility.

It is important to understand that theIPs have the same optimal objective value, but the LPs have different values—one providesa weaker LP bound than the other.

Some of the earliest exact algorithms involve simply solving the IP usingbranch-and-bound

Therefore, a number of other optimal approaches were developed. Two ofthese—Lagrangian relaxation and a dual-ascent method called DUALOC—are discussedin Sections 8.2.3 and 8.2.4, respectivel

8.2.3 Lagrangian Relation

One of the methods that has proven to be most effective forthe UFLP and other location problems is Lagrangian relaxation, a standard technique forinteger programming

Lagrangian relaxation is to remove a set of constraints to create a problem that’seasier to solve than the original.

by adding a term that penalizes solutions for violating theconstraints

When the upper and lower bounds are close (say, within1%), we know that the feasible solution we have found is close to optima

We relax constraints (8.4), removing them from the problem andadding a penalty term to the objective function:

\[ \sum\limits_{j \in J} \lambda_i (1-y_{ij}) \]

The $\lambda_i$ are called Lagrange multipliers.

For now, assume λ is fixed. Relaxing constraints (8.4) gives us the following problem,known as the Lagrangian subproblem: The Lagrangian subproblem :

\[ \begin{align} \min &\sum\limits_{j\in J} f_j x_j + \sum\limits_{i\in I} \sum\limits_{j\in J} h_i c_{ij} y_{ij} +\sum\limits_{j \in J} \lambda_i (1-y_{ij}) \\ &= \sum\limits_{j\in J} f_j x_j + \sum\limits_{i\in I} \sum\limits_{j\in J} (h_i c_{ij} -\lambda_i) y_{ij} +\sum\limits_{j \in J} \lambda_i \end{align} \]

subject to

\[ \begin{align} y_{ij} &\leq x_j &\forall i \in I, \forall j \in J \\ x_j &\in\{0, 1\} &\forall j \in J \\ y_{ij} &\ge 0 & \forall i \in I, \forall j \in J \end{align} \]

It turns out that the problem is quite easy to solveby inspection—we don’t need to use an IP solver or any sort of complicated algorithm.

The point of Lagrangian relaxation is not to generate feasible solutions, since the solutionsto (UFLP-LRλ) will generally be infeasible for (UFLP). Instead, the point is to generategood (i.e., high) lower bounds in order to prove that a feasible solution we’ve foundsome other way is good.

8.2.4 The DUALOC Algorithm

8.3 Other Minisum Models

The UFLP is an example of a minisum location problem. Minisum models are so calledbecause their objective is to minimize a sum of the costs or distances between customers andtheir assigned facilities

covering location problems are more concerned with the maximum distance, with the goalof ensuring that most or all customers are located close to their assigned facilities

minisum models are more commonlyapplied in the private sector, in which profits and costs are the dominant concerns, andcovering models are most commonly applied in the public sector, in which service, fairness,and equity are more important

8.3.1 The Capacitated Fixed-Charge Location Problem

The UFLP can be easilymodified to account for capacity restrictions; the resulting problem (not surprisingly) iscalled the capacitated fixed-charge location problem, or CFLP.

8.4 Covering Models

fire departments should have the objective of arriving to afire within 4 minutes of receiving a call

ince the optimal solutions to those problems may assign some customers tovery distant facilities if it is cost effective to do so

Instead, we need to use the notion ofcoverage, which indicates whether a given customer is within a prespecified distance, orcoverage radius, of an open facility.

we discuss three seminal facility location models that use coverage todetermine the quality of the solution 1. Set covering location problem (SCLP): locates the minimum number of facilities to cover every demand node 2. maximal covering location problem (MCLP): covers as many demands as possible while locating a fixed number of facilities. 3. p-center problem: locates a fixed number of facilities to minimize the maximum distance from a demand node to its nearest open facility.

8.4.1 The Set Covering Location Problem

In the set covering location problem (SCLP), we are required to cover every demand node;the objective is to do so with the fewest possible number of facilities. Parameters: - $a_{ij}=1$ : if facility $j\in J$ can cover customer $i\in I$ (if it is open), 0 otherwise.

The coverage parameter $a_{ij}$ can be derived from a distance or cost parameter such as $c_{ij}$ in the UFLP,

Then, the SCLP can be formulated as follows: \[ \min \sum\limits_{j \in J} x_j \] subject to $$ \[\begin{align} \sum\limits_{j\in J} a_{ij} x_j & \ge 1 &\forall i \in I \\ x_j & \in \{0, 1\} &\forall j \in J \end{align}\] $$

Sometimes we wish to minimize the total fixed cost of the opened facilities, rather than the total number, in which case the following objective function is appropriate \[ \min \sum\limits_{j \in J} f_j x_j \]

8.4.2 The Maximal Covering Location Problem

The maximal covering location problem (MCLP) seeks to maximize the total number ofdemands covered subject to a limit on the number of open facilities.