This blog is the learning notes for preparing the preliminary exams of Queue theory, referring to Fundamentals of queueing theory
- Shortle, J. F., Thompson, J. M., Gross, D., & Harris, C. M. (2018). Fundamentals of queueing theory (Vol. 399). John Wiley & Sons.
1. Introduction
Queueing theory attempts to answer these questions through detailed mathematical analysis
There are many valuable applications of queueing theory including traffic flow(vehicles, aircraft, people, communications), scheduling (patients in hospitals, jobson machines, programs on a computer), and facility design (banks, post offices, amusement parks, fast-food restaurants).
Note: 本文文字部分借助
obsidian+Annotator插件（Annotator介绍见 obsidian-annotator)，实现markdown文件中。图片部分借助Image auto upload plugin插件 （见 Link ）和PicGo实现图片自动上传到GitHub图床。然后借助python实现简单的文本内容提取，就可以得到纯净的笔记内容。具体 操作和实现流程，见之前博客Photography-is-simple/的引言部分教程。完整笔记链接见： Download Now
1.1 Measures of System Performance
Figure 1.1 shows a typical queueing system: Customers arrive, wait for service, receive service, and then leave the system. What might one like to know about the effectiveness of a queueing system? Generally there are three types of system responses of interest:
- 顾客的等待时间：waiting time that a typical customer might endure,
- 队列或系统中累积的顾客数：the number of customers that may accumulate in the queue or system,
- 服务员的空闲时间：idle time of the servers.
Since most queueing systems have stochastic elements, these measures are often random variables, so their probability distributions – or at least their expected values – are sought
waiting times, there are two types – the time a customer spends in the queue and the total time a customer spends in the system (queue plus service) Notation: - \(W_q\) : The average waiting time of a typical customer in queue; - \(W\) : The average waiting time in the system; - \(L_q\) : The average number of customers in the queue; - \(L\) : The average number of customers in the systems;
there are two customer accumulation measures – the number of customers in the queue and the total number of customers in the system
The task of the queueing analyst is generally one of two things – to determine some measures of effectiveness for a given process or to design an “optimal” system according to some criterion.
To design the waiting facility, it is necessary to have information regarding the possible size of the queue .
Ultimately, the issue generally comes down to a trade-off between better customer service and the expense of providing more service capability, that is, determining the increase i ninvestment of service for a corresponding decrease in customer delay
1.2 Characteristics of Queueing System
A quantitative evaluation of a queueing system requires a
mathematical characterization of the underlying processes. In many
cases, six basic characteristics provide an adequate description of the
system: In many cases, six basic characteristics provide an adequate
description of the system: 1. 顾客的到达过程 Arrival pattern of
customers
2. 服务员的服务过程 Service pattern of servers
3. 服务员的数量和服务通道的数量 Number of servers and service
channels
4. 排队规则 System capacity
5. 系统容量 Queue discipline
6. 服务阶段的数量 Number of service stages
1.2.1 Arrival Pattern of Customers
A common arrival process is the Poisson pro-cess, which will be described in Section 2.2
An arrivalpattern that does not change with time (i.e., the probability distribution describingthe input process is time-independent) is called a stationary arrival pattern. Onethat is not time-independent is called nonstationary. - 止步 (balked)
If a customerdecides not to enter the queue upon arrival, the customer is said to have balked. - 中途退出 （Reneged)
Acustomer may enter the queue, but after a time lose patience and decide to leave. Inthis case, the customer is said to have reneged - 换队 (jockey)
In the event that there are two or moreparallel waiting lines, customers may switch from one to another, that is, jockey forposition
1.2.2 Service Patterns
One generally thinks of one customer beingserved at a time by a given server, but there are many situations where customersmay be served simultaneously by the same server - 状态相依服务 (state-dependent service)
The situation in which service depends on the number ofcustomers waiting is referred to as state-dependent service
1.2.3 Number of Servers
Thus, when specifying the number ofparallel servers, we typically assume that the servers are fed by a single line. Also,it is generally assumed that the servers operate independently of each other.
1.2.4 Queue Discipline
Queue discipline refers to the manner in which customers are selected for servicewhen a queue has formed. 常见的排队规则： - FCFS : first come first served 先到先服务 - LCFS : last come first served 后到先服务 - RSS : random selection for service 随机服务 - PS : processor sharing 处理器共享 - pooling : 轮询（一个服务员 为多个序列的顾客提供服务，先服务第一队列的顾客吗，然后服务第二个队列的顾客，以此类推）
There are two general situations in priority disciplines, preemptive andnonpreemptive. - 非抢占情形 具有最高优先级的顾客排在队列的最前面，但要一直等到当前正在服务的顾客的服务结束后，顾客才能接受服务，即使正在接受服务的顾客优先级更低； - 抢占情形 即使优先级较低的顾客已经在接受服务，也允许优先级较高的顾客在到达时立即接受服务，中断服务员对该优先级顾客的服务，只有高优先级顾客接受完成服务后，该低优先级顾客才能继续接受服务。这时又有两种情形： - 该顾客可以从被抢占的时刻继续接受服务； - 重新开始接受服务
1.2.5 System Capacity
These are referred to as finite queueingsituations; that is, there is a finite limit to the maximum system size.
1.2.6 Stages of Service
Recycling is commonin manufacturing processes, where quality control inspections are performed aftercertain stages, and parts that do not meet quality standards are sent back for repro-cessing.
1.2.7 Notation
As shorthand for describing queueing processes, a notation has evolved, due for themost part to Kendall (1953), which is now rather standard throughout the queueingliterature A queueing process described by a series of symbols and slashes (斜线) \(A/B/X/Y/Z\) : - \(A\) : denotes the inter-arrival time distribution (到达时间间隔分布) - \(B\) : service time distribution (服务时间分布)
- 例子
通常，如果系统容量没有限制，即 \(Y =\infty\)），则省略系统容量的符号；如果排队规则是先到先服务（Z=FCFS），则省略排队规则的符号。因此 \(M/D/2/\infty/\text{FCFS}\) 和 \(M/D/2\) 表达的含义相同。
Rather, M is used, standing for the Markovian or memoryless propertyof the exponential (described in Section 2.1)
1.2.8 Model Selection
If customers choose a checkout counter on a purely random basis (withoutregard to the queue length in front of each counter) and never switch lines (nojockeying), then we have c independent single-server models.
As jockeying is rather easy to accomplish in supermarkets, the c-servermodel with one queue may be more appropriate and realistic than c independentsingle-server models, which one might have been tempted to choose initially prior togiving much thought to the process.
1.3 The Experience of Waiting
This section summarizes several principles, proposed by Maister (1984),related to the experience or psychology of waiting. 1. Unoccupied time feels longer than occupied time. 2. Pre-process wait feels longer than in-process wait. 3. Anxiety makes waiting seem longer. 4. Uncertain waits are longer than known, finite waits. 5. Unexplained waits are longer than explained waits. 6. Unfair waits are longer than equitable waits. 7. Longer waits are tolerable for more valuable service. 8. Solo waits feel longer than group waits.
1.4 Little's Law
A fundamental relationship that is used extensively in queueing
theory and throughoutthis text is Little’s law. Little’s law provides a
relationship between three fundamental quantities: The average rate
\(λ\) that customers arrive to a
system, the average time \(W\) that a
customer spends in the system, and the average number \(L\) of customers in the
system. \[
L = \lambda W
\]
The second limit W is thelong-run average time spent in the system per customer. The third limit L is thelong-run average number of customers in the system
Theorem 1.1 [Little’s law] If the limits \(λ\) and W in (1.1) exist and are finite, thenthe limit \(L\) exists and
Before giving examples, we make some general remarks about Little’s law.
在给出例子之前，需要对 Little 法则进行一些一般性的解释说明： 1. 定理用于计算长期平均值，即式中的 \(L, \lambda, W\) 被定义为无穷极限； 2. 定理要求 \(\lambda\) 和 \(W\) 有极限存在，这就排除了当时间无限增长时系统的指标无界的情况； 3. 定理没有要求必须存在一个队列，但要求存在一个系统，顾客可以到达和离开该系统。
1.4.1 Geometric Illustration of Little's Law
We now give a geometric “proof” of Little’s law. This is not a rigorous proof, butrather a rough argument showing the main ideas behind Little’s law.
2. Review of Stochastic Processes
This chapter provides an overview of key concepts in stochastic processes usedthroughout this text
2.1 The Exponential Distribution
In queueing theory, the exponential distribution is often used to model the time until aparticular event occurs
We will see (Section 2.2) that the exponential distribution isclosely connected with the Poisson process, another widely used model in queueingtheory. 定义：服从指数分布的随机变量是连续型随机变量，其 概率密度函数 pdf 为： \[ f(t) = \lambda e^{-\lambda t} \] 服从指数分布的随机变量 \(T\) 的 累积分布函数 (cumulative distribution function, CDF)、互补累积分布函数 (complementary cumulative distribution function, CCDF)、期望和方差可以通过其概率密度函数求得，分别表示为：
\[ \begin{array}{l} F(t) \equiv \operatorname{Pr}\{T \leq t\}=1-e^{-\lambda t} \\ \bar{F}(t) \equiv \operatorname{Pr}\{T>t\}=e^{-\lambda t} \\ \mathrm{E}[T]=\frac{1}{\lambda}, \quad \operatorname{Var}[T]=\frac{1}{\lambda^2} \end{array} \]
Definition 2.1 An exponential random variable is a continuous random variablewith probability density function (PDF): \[ Pr\{T>t+s|T>s\} = Pr\{T>t\}\quad (s, t \ge 0) \]
Theorem 2.1 An exponential random variable has the memoryless property
Note that \(Pr\{T > t + s, T > s\}= Pr\{T > t + s\}\) (if T is bigger than \(t + s\), then it is also bigger than \(s\)).
Theorem 2.4 Let \(T_1,\cdots,T_n\) be independent exponential random variables with rates \(λ_1,\cdots,λ_n\), respectively. Then \[ Pr\{ T_i = \min \{T_1, \cdots ,T_n\}\} = \frac{\lambda_i}{\lambda_1 + \cdots+ \lambda_n} \]
Theorem 2.5 Let T1,...,Tn be independent exponential random variables withrates λ1,...,λn, and let T = min{T1,...,Tn}. Then the event {Ti = T} isindependent of T
2.2 The Poisson Process
The Poisson process is a common process for modeling arrivals to a queueing system.Intuitively, the process can be thought of describing events that occur “randomly” intime. - Stochastic process (随机过程) \(\{N(t), t\ge 0\}\) : a collation of random variables indexed by time. - Counting process (记数过程) : a stochastic process in which \(N(t)\) takes on nonnegative integer values and is nondecreasing in time.
A counting process typicallyrepresents the cumulative number of events that have occurred by time t. With thesepreliminaries, we give a definition of the Poisson process
Definition 2.3 A Poisson process with rate \(λ > 0\) is a counting process \(N(t)\) with the following properties: 到达速率为 \(\lambda >0\) 的泊松过程，满足以下性： 1. \(N(0)=0\) 2. \(Pr\{\text{1 event between} t \text{ and } t + ∆t\}= λ∆t + o(∆t)\). 3. \(Pr\{\text{2 or more events between} t \text{ and } t + ∆t\}= o(∆t)\). 4. The numbers of events in nonoverlapping intervals are statistically independent; that is, the process has independent increments (独立增量过程).
Definition 2.4 A Poisson random variable is a discrete random variable with prob-ability mass function 泊松随机变量是离散随机变量，其概率质量函数为： \[ p^n = e^{-A} \frac{A^n}{n!}, \quad n =0,1,2, \cdots \] 其中，\(A\) 是大于 0 的常熟，泊松随机变量 \(X\) 的期望和方差分别为 \[ \mathbb {E} [X] = A, Var[X] = A \]
Poisson processes have a number of interesting additional properties, which arestated in the following theorems. The first result is that a Poisson process hasstationary increments. This means that the distribution of the number of events ina given time interval (i.e., an increment) depends on the length of the interval butdoes not depend on the absolute location of the interval in time
he notion that event times are “completely random” comes from the factthat they are uniformly distributed in time. However, we must be precise about whatwe mean by “event times.” Specifically, we must distinguish between ordered and un-ordered event times.
One important consequence of the uniform property of the Poisson process is thatthe outcomes of random observations of a stochastic process X(t) have the sameprobabilities as if the scans were taken at Poisson-selected points
Theorem 2.10 (Splitting)
Theorem 2.11 (Superposition)
2.2.1 Generalizations of the Poisson Process
The first generalization considered is a nonhomogeneous Poisson process (NHPP).A NHPP can be thought of as a Poisson process where the arrival rate λ is replaced bya time-dependent function λ(t)
Definition 2.5 A nonhomogeneous (or nonstationary) Poisson process is a Poissonprocess (Definition 2.3) in which assumption 2 is replaced by the following 非齐次泊松过程 的定义为： \[ Pr\{1 \text{ arrival between } t \text{ and } t+\Delta t \} = \lambda (t) \Delta t +o(\Delta t) \] 从定义中可以发现，其到达速率 \(\lambda (t)\) 在一天中随时间 \(t\) 变化。 Note : 当非齐次泊松过程的到达速率 \(\lambda(t)\) 是常数时，可将非齐次泊松过程视为标准泊松过程。
Theorem 2.12 For a non-homogeneous Poisson process
\(N(t)\) with mean event
rate \(λ(t)\), the number of events in
a time interval \((s,t]\) is a Poisson
random variable with mean \(m(t)
−m(s)\), where \[
m(t) \equiv \int_0^t \lambda(u) \operatorname u
\]
The difference \(m(t) - m(s)\) can be computed by integrating \(\lambda (u)\) \(@a\)
The function \(m(t)\) is sometimes called the mean value function It represents the cumulative expected number of events by time \(t\). - CPP : compound Poisson process 复合泊松分布
The next generalization is a compound Poisson process (CPP). 复合泊松分布类似于标准泊松分布，但在复合泊松分布过程中，事件按批次发生。
Definition 2.6 Let \(M(t)\) be a Poisson process, and let \({Y_n}\) be an i.i.d. sequence of strictly positive integer random variables that are independent of \(M(t)\). Then Formulation: \[ N(t) \equiv \sum\limits_{n=1} ^{M(t)} Y_n \] Example : 将一辆公交车视为一个批次，车上所有乘客在同一批次到达下一个站点。批次数 （如到达站点的公交车数） 服从泊松分布，则 到达的顾客数 （如公交车上的乘客数）服从 复合泊松分布。其中 \(M(t)\) 表示时刻 \(t\) 前到达的公交车数，\(Y_n\) 表示第 \(n\) 亮公交车上的乘客数，\(N(t)\) 表示时刻 \(t\) 前到达的总乘客数。
For a given value of t,N(t) is a compound Poisson random variable, since the number of terms in the sumis random and follows a Poisson distribution (and this number is independent of Yn) 与标准泊松过程相比，复合泊松过程具有独立且平稳的增量，但不具有 有序性，即复合泊松过程是将 Sec 2.2 定义中的性质（2）和性质（3）替换为以下性质的泊松过程： \[ Pr{i \text{ arrivals in } (t,t + ∆t]}= λi ∆t + o(∆t) \quad (i = 1,2,...), \] 其中，\(\lambda_i \equiv c_i \lambda\) 是大小为 \(i\) 的批次的 有效到达速率。
For a CPP, it is relatively straightforward to derive the mean and variance of N(t)(e.g., Ross, 2014): Mean and variance of \(N(t)\): \[ \begin{align} \mathbb{E}[N(t)] &= \lambda t \mathbb{E}[Y_n] \\ \text{Var}[N(t)] & = \lambda t \mathbb{E}[Y_n^2] \end{align} \]
- Renewal Process : 更新过程 更新过程是 非负独立同分布 随机变量的集合，这些随机变量表示连续发生的事件之间的事件间隔。
The Poisson process is special case of a larger class of problems called renewalprocesses. A renewal process arises from a sequence of nonnegative IID randomvariables denoting times between successive events.
For a Poisson process, theinter-event times are exponential, but for a renewal process, they follow an arbitrarydistribution G.
A strong argument in favor of exponential inputs is the one that often occurs in thecontext of reliability.
Here, the exponential appears quite frequently as the limitingdistribution of the (normalized) first-order statistic of random samples drawn fromcontinuous populations (see Problem 1.10 for one such example).
It is that the exponentialdistribution is the one that provides the least information, where information content 指数分布 \(f(x)\) 的信息量或负熵被定义为： \[ \int f(x) \log f(x) \operatorname d x \]
2.3 Discrete-Time Markov Chains
In this section, we consider a class of models in which the system transitions amonga discrete set of states at various points in time
Inqueueing applications, the system state is often defined as the number of customers inthe system, in which case the state space is the set of nonnegative integers 0,1,2,... 马尔可夫链的基本假设是具有 马尔可夫性，即 \[ Pr\{X_{n+1} = j|X_0 =i_0, X_1=i_1, \cdots, X_n =i_n \} = Pr\{ X_{n+1}=j|X_n=i_n\} \]
Intuitively, the Markov property states that if the “present” state of the system \((Xn)\) is known, then the “future” \((X_{n+1})\) is independent of the “past” \((X_0,...X_{n−1})\)
The conditional probabilities \(Pr\{Xn+1 = j|Xn = i\}\) are called the single-step transition probabilities or just the transition probabilities.
For a Markov chain, one may be interested in the m-step transition probabilities,defined as the probability of being in state \(j\) exactly \(m\) steps after being in state \(i\)
Let \(P^{(m)}\) be the matrix formed by the elements \(p^{(m)}_{ij}\) .From the basic laws of probability
- CK equation: 查普曼-科尔莫戈罗夫方程 (Chapman-Kolmogorov equation)
This is the matrix equivalent of thewell-known Chapman Kolmogorov (CK) equations for this Markov process
2.3.1 Properties of Markov Chains
State \(j\) is accessiblefrom state \(i (i \to j)\) if there exists an n ≥ 0 such that \(p^{(n)}_{ij} > 0\). That is, there is some path from i to j with nonzero probability 1. 如果存在 \(n\ge 0\)，使得 \(p^{(n)}_{ij} >0\)， 则系统可以从状态 \(i\) 到达状态 \(j\) (\(i \to j\))，即存在从状态 \(i\) 到状态 \(j\) 的非零概率路径。 2. 连通 (cummunicate)：如果 \(i\to j\) 且 \(j \to i\)，则称状态 \(i\) 和状态 \(j\) 是连通的 \(i \leftrightarrow j\)。 3. 等价类 (communication class)：性质2 将马尔可夫链的状态划分为多个互不相交的子集，被称为等价类。 - 一个等价类中的所有状态都是连通的，并且该等价类中的状态不与任何其他等价类中的状态想连通。 4. 不可约的 (irreducible)：如果一个马尔可夫链的所有状态都是连通的，系统可以从任意状态到达任意其他状态，则称为不可约，否则，称为 可约的 (reducible) 5. 常返的 (recurrent) ：从状态 \(j\) 除法，返回状态 \(j\) 的概率为 1；否则称状态 \(j\) 为 瞬时的 (transient)
More precisely, let \(f^{(n)}_{jj}\) be the probability that a chain starting in state \(j\) returns for the first time to \(j\) in n transitions. The probabilitythat the chain ever returns to \(j\) is 设马尔可夫链从状态 \(j\) 除法，转移 \(n\) 步之后首次返回状态 \(j\) 的概率为 \(f^{(n)}_{jj}\)，则该链返回状态 \(j\) 的状态之和为 \[ f_{jj} = \sum\limits_{n=1}^\infty f^{(n)}_{jj} \] 如果 \(f_{jj}=1\)，则状态 \(j\) 是常返的；如果 \(f_{jj}<1\) ，则状态 \(j\) 是瞬时的。当 \(f_{jj} = 0\) 时， \[ m_{jj} = \sum\limits_{i=1}^\infty nf^{(n)}_{jj} \] 表示 平均回转时间 (mean recurrence time)。此时，又有以下分类： 7. 正常返的 (positive recurrent) ：\(m_{jj}<\infty\) 8. 零常返的* (positive recurrent) ：\(m_{jj}=\infty\)
The period of astate j is the greatest common divisor of integers m such that p(m)jj > 0. A state withperiod 1 is said to be aperiodic 状态 \(j\) 的 周期 (period) 是满足 \(p_{jj}^{(m)}>0\) 的所有正整数 \(m\) 的最大公约数。周期为 1 的状态是 非周期的 (aperiodic)
2.3.2 Long-Run Behavior
the limiting matrix has the property that the rows are the same. Thismeans that, a long time into the future, the probability of being in a particular statedoes not depend on the starting state.
This particular behavior does not hold for all Markov chains. Note : 但并不是所有的马尔可夫链都有这种特殊的行为。因为 1. \(n \to \infty\) 时，\(P^n\) 并非总是收敛的； 2. 如果 \(p^n\) 收敛，矩阵每行的元素可能并不相同。 由此，可以引出马尔可夫链的长期行为相关的 3 个概念： - 极限分布 (limiting distributions) - 平稳分布 (stationary distributions) - 遍历性 (ergodicity)
This motivates discussion of three related concepts having to do withlong-run behavior, limiting distributions, stationary distributions, and ergodicity.
We start by defining the limiting probabilities of a Markov chain as 马尔可夫链的极限概率为： \[ \pi_j \equiv\lim_{n\to \infty} p^{(n)}_{ij} \]
The step of rearranging the brackets requires switching a limit and a sum. If theMarkov chain has an infinite number of states (i.e., P is an infinite-dimensionalmatrix), then this step must be justified more carefully
Theorem 2.13 An irreducible and positive recurrent discrete-time Markov chainhas a unique solution to the stationary equations 定理 对于一个不可约且正常返的离散时间马尔可夫链，一下平稳方程组有唯一解： \[ \pi = \pi P \quad \text{and} \quad \sum\limits_j \pi_j = 1 \] 即 \(\pi_j = 1/m_{jj}\)，如果该马尔可夫链是非周期性的，则极限分布存在并且与平稳分布相同。
By this theorem, there are two main ways to interpret the value of \(π_j\)
he firstinterpretation is that πj is the the long-run fraction of time spent in state j. This comesfrom the fact that πj = 1/mjj
The second interpretation is that πj is the probabilityof being in state j a long time from now Example
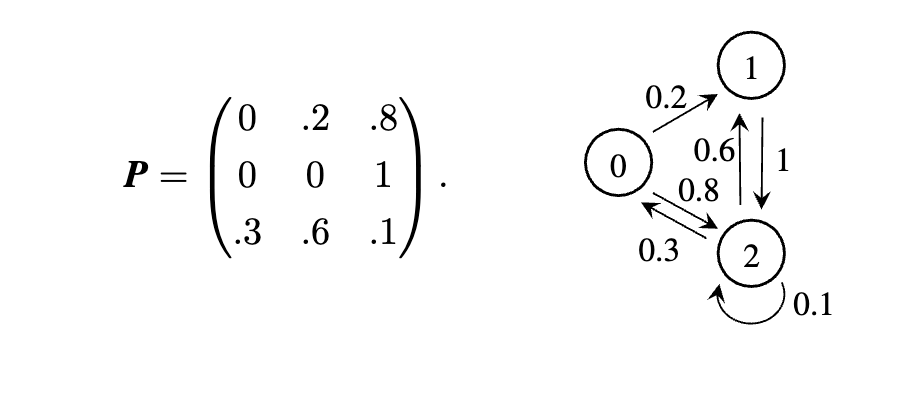
因为所有的状态都是连通的，所以该马尔可夫链是 不可约 的，且是 正常返的。具有有限状态数的不可约马尔可夫链一定是正常返的。带入上式中的平稳方程组可得： \[ \begin{cases} \pi_0 = 0.3 \pi_2 \\ \pi_1 = 0.2 \pi_0 + 0.6 \pi_2 \\ \pi_2 = 0.8 \pi_0 + \pi_1 + 0.1 \pi_2 \\ \pi_0 + \pi_1 + \pi_2 =1 \end{cases} \]
1 | import numpy as np |
Results:
1 | array([[0.17133537, 0.36886623, 0.4597984 ], |
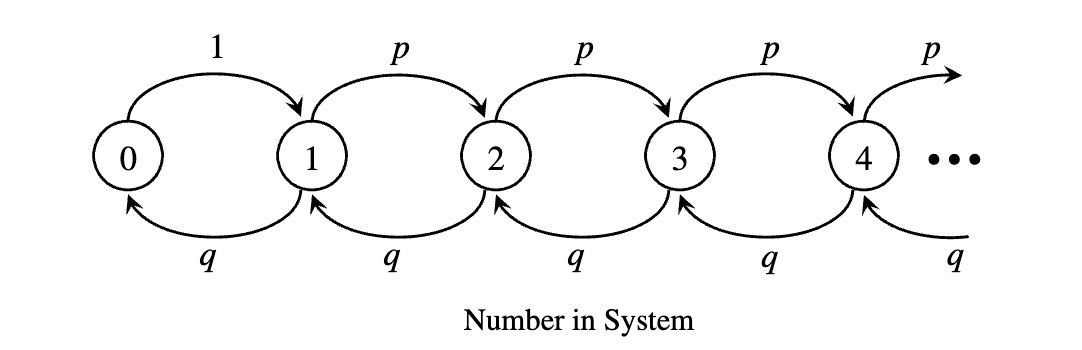
状态转移图
This chain is the embedded discrete-time Markov chain for the \(M/M/1\)queue (see Example 2.15), where the state of the system is measured onlywhen an arrival or departure occurs
The chain is irreducible and positive recurrent, so it has a unique solution tothe stationary equations.
Theorem 2.14 An irreducible, aperiodic chain is positive recurrent if there exists anonnegative solution of the system
2.3.3 Ergodicity
Closely associated with the concepts of limiting and stationary distributions is theidea of ergodicity, which has to do with the information contained in one infinitelylong sample path of a process
Ergodicity is important in that itdeals with the problem of determining measures of a stochastic process X(t) from asingle realization, as is often done in analyzing simulation output 遍历性可以帮助我们基于过程的单个样本实现来确定随机过程 \(X(t)\)的统计指标。如果 \(X(t)\) 的所有指标都可以基于过程的单个样本实现 \(X_0(t)\) 来确定或较为准确地估算，那么 \(X(t)\) 在一般意义上是 遍历的。
ince statistical measures of theprocess are usually expressed as time averages, this is often stated as follows: X(t)is ergodic if time averages equal ensemble averages.
For a nonstationary process, the ensemble average m(t) might be different atdifferent values of t. For example, if a queueing system starts in an empty state, thenthe ensemble average at t = 0 will be different than the ensemble average at somelarge value of t, where the system is in steady state
That is, the ensemble average m(t) converges to a limit as \(t → ∞\) and this limitingvalue equals the time average
We now discuss the link between a limiting distribution, a stationary distribution, and ergodicity. Consider a DTMC that is irreducible and positive recurrent. Such a chain has a unique stationary distribution {\(π_i\)} by Theorem 2.13
2.4 Continuous Time Markov Chains
2.4.1 Embedded Markov Chains
A (time-homogeneous) continuous-time Markov chain (CTMC) is a
stochastic pro-
cess {\(X(t),t \ge 0\)} with a
countable state space, such that:
1. Each time the process enters state \(i\), it remains in that state for a period
of time that is exponentially distributed with rate \(v_i\) (independent of the past).
2. When the process departs state \(i\), it goes to state \(j \neq i\) with probability \(p_{ij}\) (independent of the past).
Note : 连续时间（齐次）马尔可夫 （CTMC）从一个状态转移到另一个状态的过程与离散时间马尔可夫链 （DTMC）相似，但是 CTMC 在每个状态停留的时间是 连续型指数随机变量。由 转移矩阵 \(\{ p_{ij}\}\) 定义的 DTMC 被称为嵌入离散时间马尔可夫链（embedded discrete-time Markov chain）。
In continuous time, the Markov property can be stated as 在连续时间上， 马尔可夫性可以表述为： \[ Pr\{ X(t+s) = j | X(t)=i, X(u), 0\leq u<t\} = Pr \{X(t+s) = j|X(t) = i\} \]
2.4.1 Embedded Markov Chains
In many of the situations in this text requiring the use of a continuous-time queueingmodel, we can often get satisfactory results by looking at the state of the systemonly at certain selected times 在许多场景中，要求使用连续时间排队模型，在这些场景下，通常需要在特定时间点观察系统的状态，由此，引入 嵌入离散时间马尔可夫链 来解决此类问题。
As discussed previously, if the system is in state i ≥1, the next event is an arrival with probability λ/(λ+μ) and a service completion with probability μ/(λ+μ).
More generally, there are some continuous-time processes that arenot CTMCs but still have embedded discrete-time Markov chains.
2.4.2 Chapman-Kolmogoroc Equations
For a DTMC, we were able to determine the n-step transition probabilities via theChapman–Kolmogorov equations.
Theorem 2.15 Let \(p_i(t)\) be the probability that the system is in state i at time \(t\), let \(p(t)\) be the vector (\(p_0(t),p_1(t),\cdots\)), and let p′(t) be the vector of its derivatives.Then 定理 设 \(p_i(t)\) 为系统在时刻 \(t\) 处于状态 \(i\) 的概率， \(p(t)\) 表示向量 \((p_0(t),p_1(t),\cdots)\)，且 \(p^\prime(t)\) 为 \(p(t)\) 的导数，则： \[ p^\prime(t) = p(t) Q \] 其分量形式为： \[ p_j^\prime(t) = -v_j p_j(t) + \sum\limits_{r\neq j} p_r(t) q_{rj} \]
2.4.3 Long-Run Behavior
The same concepts of stationarity and steady state apply for the continuous-timecase, with t replacing n in the limiting process.
Theorem 2.16 For a continuous-time Markov chain, if the embedded discrete-timechain is irreducible and positive recurrent, then there is a unique solution to the 定理 2.16 对于一个连续时间马尔可夫链，如果其对应的嵌入离散时间马尔可夫链是不可约且正常返的，那么以下平稳方程组存在唯一解： \[ \begin{cases} 0 = pQ\\ \sum\limits_j p_j =1 \end{cases} \] 其中，\(0\) 是零向量。
Compared to a discrete-time chain (Theorem 2.13), aperiodicity is not required forthe limiting distribution to exist in a continuous-time Markov chain
3. Simple Markovian Queueing Models
Recall that a birth death process is a specific type ofcontinuous-time Markov chain whose structure leads to a straightforward solutionfor the steady-state probabilities {\(p_n\)}
Webegin with the general theory of birth death process. Then we apply these results toobtain measures of effectiveness for the queueing systems given above
3.1 Birth-Death Processes
A birth death process consists of a set of states {0, 1, 2, . . . },
typically denoting the“population" of some system 
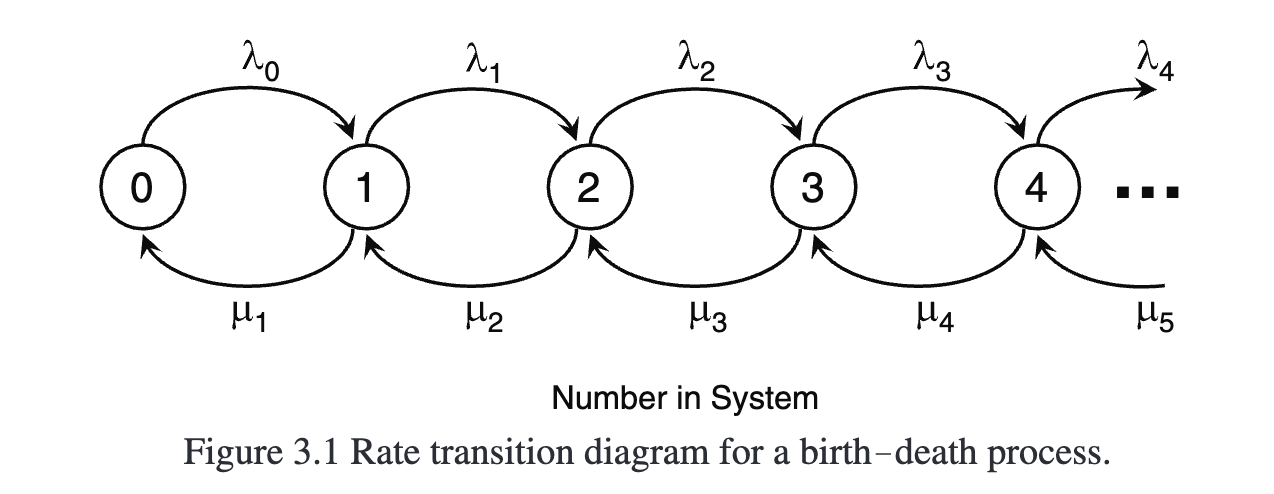
从 Sec 2.4.3 定理2.16 中可知，该系统存在一个解，基于 \(0=pQ\)，且当 \(\lambda_n\) 和 \(\mu_n\) 有一定的条件限制时，可以求得该解。对于生灭过程，向量矩阵的分量形式为： \[ \begin{align} 0 & = -(\lambda_n +\mu_n) p_n +\lambda_{n-1} p_{n-1} + \mu_{n+1} p_{n+1} \\ 0 & =-\lambda_0 p_0 + \mu_1 p_1 \end{align} \] 也可以写为（流量平衡，flow balance）： \[ \begin{align} (\lambda_n +\mu_n) p_n & =\lambda_{n-1} p_{n-1} + \mu_{n+1} p_{n+1} \\ 0 & =-\lambda_0 p_0 + \mu_1 p_1 \end{align} \] 第一个式子左边表示从状态 \(n\) 转移 出去 的速率，右边表示从其他状态 进入 状态 \(n\) 的速率。
These equations can also be obtained using the concept of flow balance. The basicidea is this: In steady state, the rate of transitions out of a given state must equal therate of transitions into that state. 求解可以得到： \[ p_n= \frac{\lambda_{n-1} \lambda_{n-1}\cdots \lambda_0}{\mu_n\mu_{n-1}\cdots\mu_1} p_0 = p_0 \prod_{i=1}^n \frac{\lambda_{i-1}}{\mu_i} ,\quad n\ge 1 \] 进而可以求解得到： \[p_o = \left( 1+\sum\limits_{n=1}^\infty \prod_{i=1}^n \frac{\lambda_{i-1}}{\mu_i}\right)^{-1}\]
we see that a necessary and sufficient condition for the existence of asteady-state solution is the convergence of the infinite serie 可以发现，稳态存在解的充要条件是以下无穷级数收敛： \[ 1+\sum\limits_{n=1}^\infty \prod_{i=1}^n \frac{\lambda_{i-1}}{\mu_i} \]
The equations in (3.1) are called global balance equations, since they equate the total mean flow into each state with the total mean flow out of that state 两种不同思路： - 上述方法称为 整体平衡方程 (global balance equation) - 局部平衡方程 (detailed balance equation) 。正如稳态时 流入和流出 一个状态的平均流量必须相等，稳态时向左和向右通过分界线的平均流量也必须相等。如下图
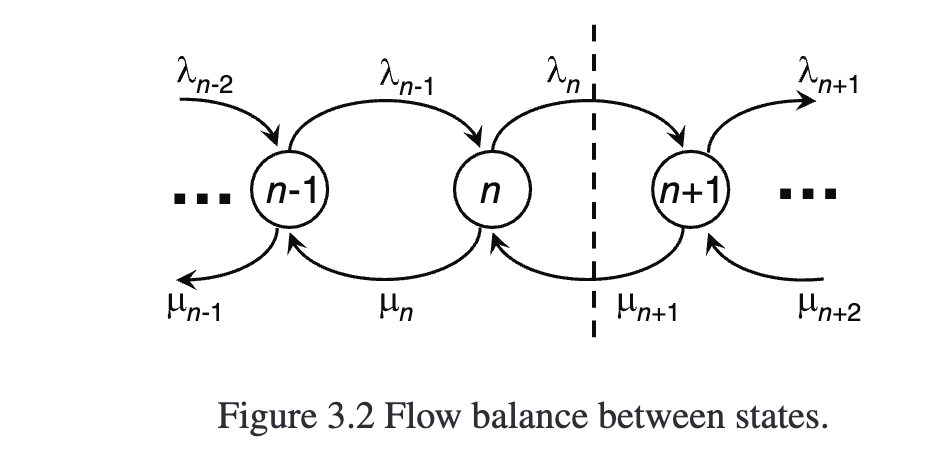
we can know: \[ \begin{align} \lambda_{n-1} p_{n-1} &= \mu_n p_n \\ p_n & = \frac{\lambda_{n-1}}{\mu_n} p_{n-1} \end{align} \]
Just as mean flows into and out of a state must be equal in steady state, so alsomean flows across the barrier must be equal in steady state. - 可逆性 (reversibility)
It is not true for all Markov chains that the mean flows between two states areequal.
The equating of these adjacent flows relates to something called reversibility,a concept that becomes particularly useful later in our work on queueing networks
or more general Markovian models, this is not necessarilytrue. However, for all Markovian models, equating the total flow out of a state withthe total flow into the state always yields the global balance equations Note : 并非所有马尔可夫链的两个状态之间的 平均流量 都想等 （与 可逆性 有关）。但是，对于所有马尔可夫过程，流出一个状态的总流量与流入该状态的总流量想等，所以一定可以得到整体平衡方程，从而可以求得 \(\{p_n\}\)。
3.2 Single Server Queues (\(M/M/1\))
更多知识查看：Queue-Theory
有三种方法求解 \(\{p_n\}\)： 1. 迭代法 Iterative Method 2. 母函数法 Generating Functions 3. 线性算子 Operators
In summary, the full steady-state solution for theM/M/1 system is the geometric probability function 得到 \(\{p_n\}\) 为 \[ p_n = (1-\rho) \rho^n \]
We emphasize that the existence of a steady-state solution depends on the conditionthat ρ < 1, or equivalently, λ < μ .
Finally, we note that for some models, it is relatively easy to find a closed expression for \(P(z)\), but quite difficult to find its series expansion to obtain the {\(p_n\)}
3.2.4 Measures of Effectiveness
The steady-state probability distribution for the system size allows us to calculatethe system’s measures of effectiveness. - 系统中平均顾客数 \(L\) 可以根据系统的稳定概率分布来计算系统的效益指标。首先考虑当系统处于稳态时，系统中顾客数的期望和队列中顾客数的期望。
设随机变量 \(N\) 表示稳态时系统中的顾客数，\(L\) 表示其期望，则 \[ \begin{align} L &= \mathbb{E}[N] = \sum\limits_{n=0}^\infty n p_n \\ & = (1-\rho)\sum\limits_{n=0}^\infty n \rho^n \\ \\ & =\rho(1-\rho) \sum\limits_{n=0}^\infty n \rho^{n-1} \\ & = \rho(1-\rho) \left(\frac{1}{1-\rho} \right)^\prime \\ &= \frac{\rho(1-\rho)}{(1-\rho)^2} \\ & = \frac{\rho}{1-\rho} = \frac{\lambda}{\mu - \lambda} \end{align} \]
平均队列长度 \(L_q\) \[ \begin{align} L_q &= \sum\limits_{n=1}^\infty (n-1) p_n \\ & = \sum\limits_{n=1}^\infty n p_n - \sum\limits_{n=1}^\infty p_n = L _ (1-p_0) \\ & = \frac{\rho}{1-\rho} -\rho \\ & =\frac{\rho^2}{1-\rho}=\frac{\lambda^2}{\mu(\mu-\lambda)} \end{align} \]
队列不为空时的平均队列长度 \(L_q^\prime\) \[ \begin{align} L_q^\prime &= \mathbb{E}[N_q | N_q \neq 0] = \sum\limits_{n=1}^\infty (n-1) p_n^\prime = \sum\limits_{n=2}^\infty (n-1) p_n^\prime \end{align} \] 其中，\(p_n^\prime\) 表示队列不为空时的条件下系统的顾客数为\(n\) 的条件概率。 \[ \begin{align} p_n^\prime & = \frac{Pr\{n \text{ in system and }n \ge 2\}}{Pr\{n \ge 2\}} \\ & =\frac{p_n}{\sum\limits_{n=2}^\infty p_n} \quad (n \ge 2) \\ & =\frac{p_n}{1 - p_0 -p_1} =\frac{p_n}{1-(1-\rho) - (1-\rho)\rho} \\ & = \frac{p_n}{\rho^2} \end{align} \] Then \[ \begin{align} L_q^\prime &= \sum\limits_{n=2}^\infty (n-1) p_n^\prime \\ & = \sum\limits_{n=2}^\infty (n-1) \frac{(1-\rho)\rho^n}{\rho^2} \\ &= (1-\rho)\sum\limits_{n=2}^\infty (n-1) \rho^{n-2}\\ \\ &= (1-\rho)\left( \sum\limits_{n=0}^\infty n \rho^{n-1} \right) \\ &= (1-\rho)\left( \frac{1}{1-\rho} \right)^\prime\\ \\ & = \frac{1}{1-\rho} = \frac{\mu}{\mu-\lambda} \end{align} \]
顾客在系统中的平均等待时间 \(W\) \[ W = \frac{L}{\lambda} = \frac{\rho}{\lambda(1-\rho)} = \frac{1}{\mu-\lambda} \]
队列中的平均等待时间 \(W_q\) \[ W_q = \frac{L_q}{\lambda} = \frac{\lambda}{\mu(\mu-\lambda)} = \frac{\rho}{\mu-\lambda} \]
3.2.5 等待时间的分布
- 等待总时间的分布 在系统中的总等待时间为服从期望为 \(1/(\mu-\lambda)\) 的指数分布随机变量，即： \[ \begin{align} W(t) & = 1- e^{-(\mu-\lambda)t}, &t\ge0 \\ w(t) & = (\mu-\lambda)e^{-(\mu-\lambda)t}, &t>0 \\ \end{align} \]
- 排队时间的分布 可以看作是按照 \(\rho\) 的概率服从指数分布，\(1-\rho\) 的概率排队时间为 0 \[ W_q(t) = 1-\rho + \rho(1- e^{-(\mu-\lambda)t})=1 - \rho e^{-(\mu-\lambda)t} \]
\[ f(W_s) = (\mu-\lambda) e^{-(\mu-\lambda)t} \]