Large-lm-7-Mixed-Framework

9. 新的模型架构

通过前文的学习，我们知道神经预言模型的核心借口是一个将 token 序列映射到上下文嵌入的编码器：

$\text{the}, \text{mouse}, \text{ate}, \text{the}, \text{cheese}] \stackrel{\phi}{\Rightarrow} \left[\binom{1}{0.1}, \binom{0}{1}, \binom{1}{1}, \binom{1}{-0.1}, \binom{0}{-1} \right].$

以 GPT-3 为例，它是一个通过堆叠 96 层 Transformer block，映射 token 序列 $x_{1:L}$ 的神经语言模型：

$\text{GPT-3}(x_{1:L}) = \text{TransformerBlock}^{96}(\text{EmbedTokenWithPosition}(x_{1:L})),$

其中，每层Transformer block使用

• 自注意力层，允许每个token 进行交互；
• 前馈层，独立处理每个 token。

这种稠密的 Transformer 模型架构是目前开发大语言模型的主要范式。但是，扩展这种模型并非易事，需要数据、模型和流水并行。

现状：

• 我们的规模已经到了极限。

• 随着模型越来越大，它们必须被拆分到更多的机器上。下面是一个模型并行示例（具体细节见上一章）：

  \begin{align*} \text{GPU1}[\text{layer1}, \text{layer2}] \\ \text{GPU2}[\text{layer3}, \text{layer4}] \\ \text{GPU3}[\text{layer5}, \text{layer6}] \end{align*}

因此，如果我们要继续扩大规模，我们需要重新思考如何构建大语言模型。对于稠密的 Transformer 模型，每个输入使用语言模型的相同（所有）参数（如 GPT-3 的 175B 参数）。

相反，我们是否可以让每个输入使用不同的（更小的）参数子集？在本章中，我们将探讨两种不同类型的“新”模型架构，这提高了模型的规模上限。特别地，我们将讨论：

• 混合专家模型：创建一组专家，每个输入只激活一小部分专家。

  • 直觉：类似于咨询委员会，每个专家有不同的背景（如历史、数学、科学等）。

  $\text{input} \quad\quad\Rightarrow\quad\quad \text{expert}_1 \quad \text{expert}_2 \quad \text{expert}_3 \quad \text{expert}_4 \quad\quad\Rightarrow\quad\quad \text{output}.$

• 基于检索的模型：借助原始数据存储库，给定新输入，从中检索与它相关的部分，并使用它们来预测输出。

  • 直觉：借助网络搜索查询问题的答案。

  $\text{store} \quad\quad|\quad\quad \text{input} \quad\quad\Rightarrow\quad\quad \text{relevant data from store} \quad \quad\quad\Rightarrow\quad\quad \text{output}.$

9.1 混合专家模型

9.1.1 基础知识

混合专家的想法可以追溯到 Jacobs et al. (1991)。

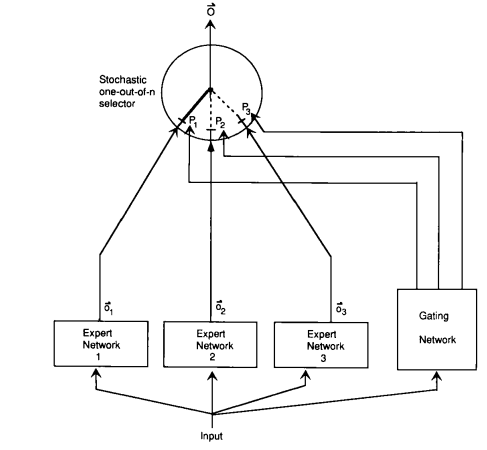
以预测问题为例：

$x \in \mathbb{R}^d \Rightarrow y \in \mathbb{R}^d.$

让我们从学习前馈（ReLU）神经网络开始：

$h_\theta(x) = W_2 \max(W_1 x, 0),$

其中参数为 $\theta = (W_1, W_2)$。然而，这个函数可能表达能力不足。因此，可以使神经网络更宽或更深。

专家的混合方法步骤如下：

• 定义 $E$ 个专家。

• 每个专家 $e = 1, \dots, E$ 都具有自己的嵌入 $w_e \in \mathbb{R}^d$。

• 将门控函数定义为 $E$ 个专家上的概率分布：

  $g_e(x) = \frac{\exp(w_e \cdot x)}{\sum_{e' = 1}^E \exp(w_{e'} \cdot x)}.$

• 每个专家 $e = 1, \dots, E$ 都具有自己的参数 $\theta^{(e)} = (W_1^{(e)}, W_2^{(e)})$。

• 根据专家特定参数定义每个专家函数：

  $h_{\theta_e}(x) = W_2^{(e)} \max(W_1^{(e)} x, 0).$

• 将最终函数定义为专家的混合：

  $f(x) = \sum_{e=1}^E \underbrace{g_e(x)}_\text{gating} \underbrace{h_{\theta_e}(x)}_\text{expert}.$

示例

考虑d=2，并且每个专家都是一个线性分类器（来源）：

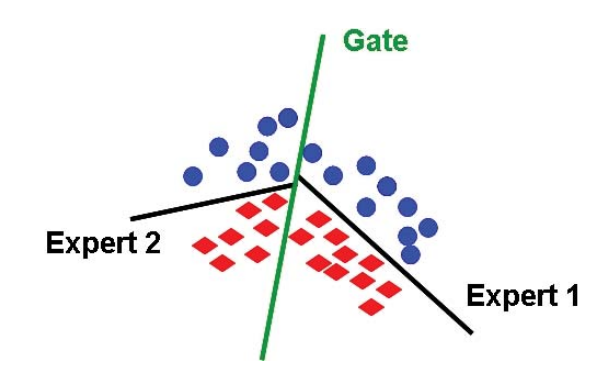
• 训练

  可以通过反向传播来学习混合专家模型。根据链式法则，可以得到：

  $\nabla f(x) = \sum_{e=1}^E g_e(x) (\nabla (\log g_e(x)) h_{\theta_e}(x) + \nabla h_{\theta_e}(x)).$

  注意到，梯度与 $g_e(x)$ 成比例，并且同时更新门控函数和专家。

• 节约计算

  门控函数 $g(x) = [g_1(x), \dots, g_E(x)]$ 对于每个专家都是非零的。例如：

  $g(x) = [0.04, 0.8, 0.01, 0.15].$

  • 专家的混合不会节省任何计算，因为前向传播仍然需要评估每个专家，而反向传播也必须接触每个专家。

  • 如果将门控函数 $g(x) = [g_1(x), \dots, g_E(x)]$ 近似为 $\tilde g(x) = [\tilde g_1(x), \dots, \tilde g_E(x)]$，其中大多数专家都是零。因此，在前向和反向传播时，只需要使用非零 $\tilde g_e(x)$ 的专家 $e$。

  例如，我们可以选取值排名前两位（top 2）的专家，并重新规范化：

  $\tilde g(x) = [0, 0.84, 0, 0.16].$

• 平衡专家

  • 只有所有专家都参与进来，混合专家才有效。
  • 如果只有一个专家处于活跃状态（例如，$g(x) = [0, 1, 0, 0]$)，那么这就是浪费。
  • 如果一直处于这种状态，那么未使用的专家的梯度将为零，因此他们将不会收到任何梯度并得到改善。
  • 因此，使用混合专家的主要考虑因素之一是确保所有专家都能被输入使用。

• 并行

  • 混合专家非常有利于并行。
  • 每个专家都可以放置在不同的机器上。
  • 我们可以在中心节点计算近似门控函数 $\tilde g(x)$。
  • 然后，我们只要求包含激活专家的机器（稀疏）来处理 $x$。

9.1.2 Sparsely-gated mixture of experts (Lepikhin et al. 2021)

现在，我们考虑如何将混合专家思想应用于语言模型。最简单的解决方法仍是使用 96 层 Transformer，但门控函数以某种方式应用于序列，且只在顶层进行专家的组合。因此，我们将混合专家的思想应用于每个 token和每层的 Transformer block（或隔层使用）

由于前馈层对于每个token是独立的，因此，我们将每个前馈网络转变为混合专家（MoE）前馈网络：

$\text{MoETransformerBlock}(x_{1:L}) = \text{AddNorm}(\text{MoEFeedForward}, \text{AddNorm}(\text{SelfAttention}, x_{1:L})).$

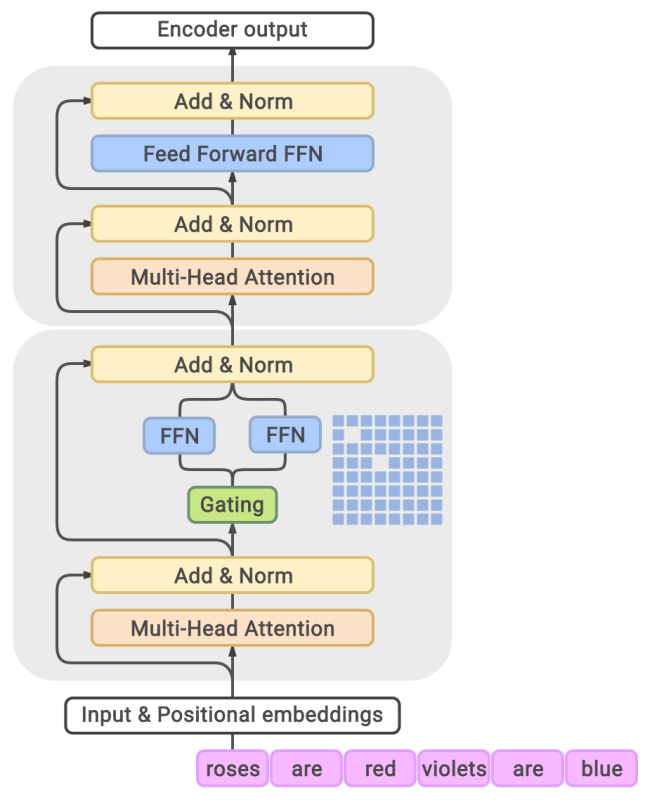
我们将 top-2 专家的近似门控函数定义如下：

• 计算第一个专家：$e_1 = \arg\max_e g_e(x)$。

• 计算第二个专家：$e_2 = \arg\max_{e \neq e_1} g_e(x)$。

• 始终保留第一个专家，并随机保留第二个专家：

  • 设 $p = \min(2 g_{e_2}(x), 1)$
  • 在概率为 $p$ 的情况下，$\tilde g_{e_1}(x) = \frac{g_{e_1}(x)}{g_{e_1}(x) + g_{e_2}(x)}, \tilde g_{e_2}(x) = \frac{g_{e_2}(x)}{g_{e_1}(x) + g_{e_2}(x)}$。对于其他专家$e \not\in \{ e_1, e_2 \}$，$\tilde g_e(x) = 0$。
  • 在概率为 $1 - p$ 的情况下，$\tilde g_{e_1}(x) = 1$。对于 $e \neq e_1$，$\tilde g_e(x) = 0 $。

具体细节如下：

1. 符号定义

   设 $B$ 是一个 batch 中的 token 数量（在所有序列中，通常在百万数量级），$E$ 是专家数目（通常在千数量级），$x_1, \dots, x_B$ 为一个 batch 中的 token。

2. 平衡专家

   设 $c_e = \sum_{i=1}^B \mathbf{1}[\tilde g_e(x_i) > 0]$ 是专家 $e$ 被选中的次数（Note：处理完一个 batch 后，$\sum_e c_e = B$）。

   • 如果所有专家都是 平衡 的，那么$c_e = \frac{B}{E}$。

   • 溢出：如果 $c_e > 2 \frac{B}{E}$，则设 $f(x) = x$（带残差的旁路），其中 2 是容量系数。

   • 辅助损失：我们期望 $c = [c_1, \dots, c_E]$ 接近均匀分布。

   我们可以惩罚 $\|c\|_2^2 = \sum_{e=1}^E c_e^2$，但这是不可微分的。

   • 定义 $m_e = \sum_{i = 1}^B g_e(x_i)$（ $c_e$ 的软版本)。

   • 在目标函数中添加 $\text{load-balancing-loss} = \sum_{e=1}^E m_e c_e$。这样，通过 $m_e$ 的梯度将为非零。

   • $\text{loss} = \text{negative-log-likelihood} + \lambda \text{load-balancing-loss}.$

     例如，取 $\lambda = \frac{0.01}{B}$。

3. 示例

   下面是一个$B=2$ 个 token，$E=4$ 个专家的例子：

   $g(x_1) = [0.2, 0.6, 0.1, 0.1] \Rightarrow \tilde g(x_1) = [0.25, 0.75, 0, 0] \\ g(x_2) = [0.1, 0.6, 0.2, 0.1] \Rightarrow \tilde g(x_2) = [0, 0.75, 0.25, 0]$

   统计为

   $c = [1, 2, 1, 0] \quad\quad\quad\quad m = [0.3, 1.2, 0.3, 0.2]$

   也就是说，我们会尝试降低专家 $2$ 的权重，避免其被过度使用。

9.1.3 Switch Transformer (Fedus et al. 2021)

定义近似门控函数 $\tilde g(x)$ 只有一个专家（获得更多稀疏性）。

技巧：

• 将 FP32 训练替换成 FP16
• 使用的较小参数进行初始化
• 专家 dropout
• 专家并行

训练了一个1.6万亿参数模型，与 T5-XXL（110亿参数）相比，训练速度提高了4倍

9.1.4 Balanced Assignment of Sparse Experts (BASE) layers (Lewis et al., 2021)

BASE 将近似门控函数 $\tilde g(x)$ 定义为对 batch 中的所有 token 进行联合优化的结果。它为每个token 分配 1 名专家，但负载平衡是一种约束，而不是软惩罚。

定义 $a = [a_1, \dots, a_B] \in \{1, \dots, E\}^B$ 作为联合分配向量。

\begin{align*} &\text{maximize} \sum_{i = 1}^B w_{a_i} \cdot x_i \\ &\text{subject to}\quad \forall e: \sum_{i=1}^B \mathbf{1}[a_i = e] = \frac{B}{E}. \end{align*}

这是一个可以有效求解的线性方程，在实践中，我们将线性方程并行化。在测试时，只需选择top 1的专家即可。

• 实验设置

  • Sparsely gated MoE (top-2 experts): 52.5B 参数
  • Switch Transformer (top-1 expert): 52.5B 参数
  • BASE (1 jointly optimized expert): 44.4B 参数 (1.3B shared 参数, 335M x 128 expert 参数)
  

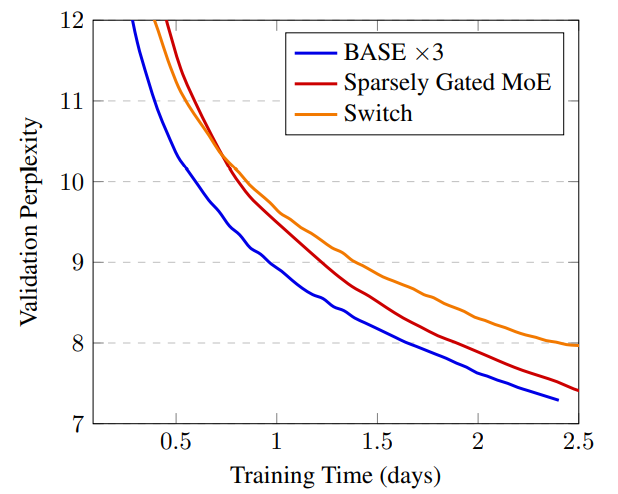
  BASE 需要更多的计算来优化 $a$，但更稳定。

• 总结和下一步工作

  • Switch Transformer（谷歌）使用了 top-1 专家。
  • BASE（Facebook）为每个 token 分配 $1$ 名专家，但进行了联合优化。

  这两个模型的性能都无法与 GPT-3 可比。虽然谷歌和 Facebook 都发布了两个最新的高性能 MoE 语言模型，它们的性能确实与 GPT-3 可比。但有趣的是，它们仍然基于最初简单的top-2专家：

  • 谷歌的 GLaM
  • 来自Facebook的 FacebookMoE

9.1.5 Generalist Language Model (GLaM) (Du et al. 2021)

规格：

• 1.2万亿个参数（GPT-3有1750亿个参数）
• 64个专家，64层，32K个隐藏单元
• 每个token激活95B（1.2T的8%）的参数

其他：

• 创建了共有 1.6 万亿个 token 的新数据集（GLaM dataset），来源包括网页、论坛、书籍、新闻等。
• 相对位置编码、门控线性单元、GeLU激活函数、RMSNorm（非 LayerNorm）
• 如果遇到 NaN/Inf，跳过权重更新/回滚到早期检查点。
• 通过仔细实施上述技巧，我们观察到，稀疏激活的模型在各个尺度上的训练都变得相当稳定。

结果：在与 GPT-3 相同的基准上进行评估（开放域问答、阅读理解、SuperGLUE等）。与 GPT-3 相比，训练成本仅为1/3，且实现了更好的0-shot和1-shot性能（尤其是在知识密集型任务中的性能）

注：他们没有在GPT-3更强的few-shot中进行评估。

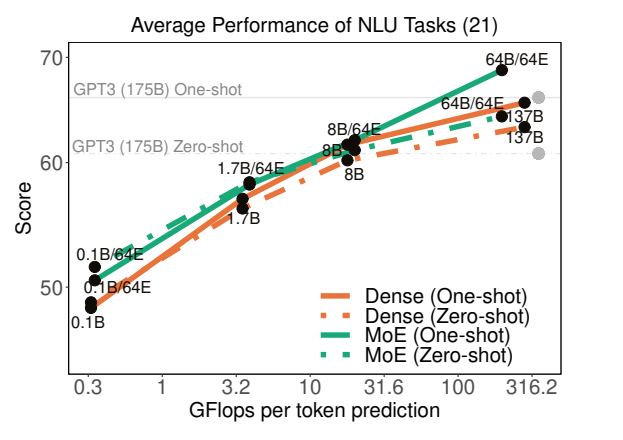
示例：

*The assistant went to work. {She brought her boss coffee., She was valued for her input.}*

刻板印象随着模型大小的增加而变得更糟（与GLaM结果相反）。

9.1.6 FacebookMoE (Artetxe et al., 2021)

• 实验设置：

  • 训练了一个1.1T参数的模型。

  • 512名专家（超过GLaM），32层，4096个隐藏单元

  • 使用112 billion token进行训练，来源包括网页、论坛、书籍、新闻等。

  • 小模型收益更大，模型越大，收益递减

  

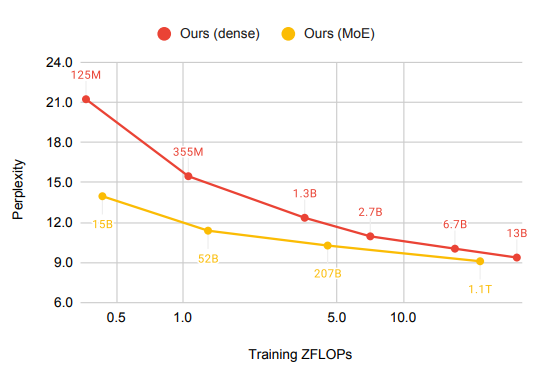
  StereoSet上的结果：

• 示例：

  *The assistant went to work. {She brought her boss coffee., She was valued for her input.}*
  
  刻板印象随着模型大小的增加而变得更糟（与GLaM结果相反）。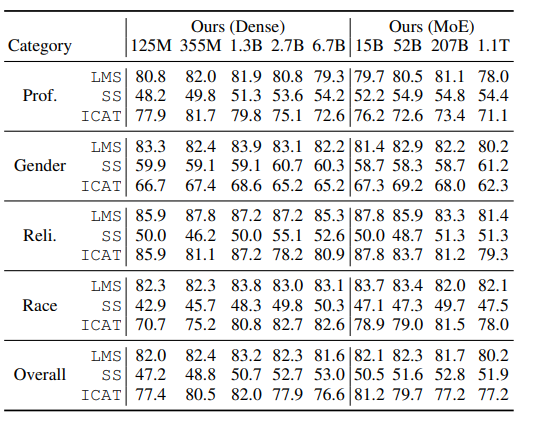

  

9.1.7 Decentralized mixture-of-experts (Ryabinin & Gusev, 2020)

• 动机

  到目前为止，混合专家纯粹是中心机构（如谷歌或Facebook）从扩大大语言模型的角度出发的。然而，混合专家自然地指示了一种更激进的权利下放。为训练 GPT-3，Azure超级计算机集群 耗资2.5亿美元。

  那么如何利用数以亿计的消费 PC 呢？

  • Folding@Home 是一个志愿者计算项目，利用世界各地的志愿者捐赠计算机进行分子动力学模拟。
  • 2020年4月，Folding@Home有70万人捐赠了产生2.43 exaFLOP（GPT-3需要350千兆FLOP）（文章）。
  • 主要区别在于分子动力学模拟计算量大，不需要网络带宽。

• 分布式哈希表：

  • $N$ 个节点
  • 单个节点需要与其他 $O(\log N)$ 节点通信
  • 使用 Kademlia DHT 协议（被 BitTorrent 和以太坊使用）
  

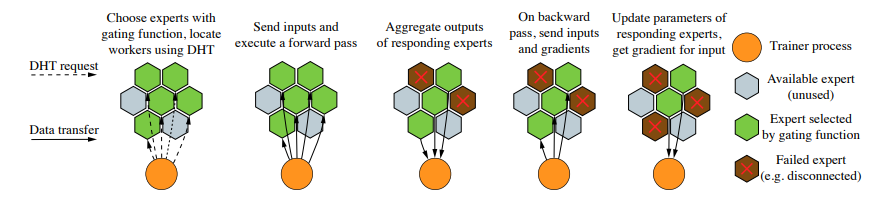
• 论文实验

  • 选取 top-4 的专家（共256名专家）
  • 每个专家都是一个 Transformer 层
  • 在4个 GPU 上训练了一个小型 Transformer LM

9.1.8 总结

• 混合专家：起源于将不同专家应用于不同输入的经典理念
• 允许训练更大的语言模型（1.1万亿个参数）
• 与稠密 Transformer 模型相比，每个输入的效率高得多（FLOP 更少）
• 效果难以比较：在相同规模上，直接比较仍然具有挑战性（GPT-3 与 GLaM 与 FacebookMoE）
• 对权力下放的重大影响

9.2 基于检索的模型

现在，我们转向基于检索的（或检索增强的、记忆增强的模型）语言模型，，它可以帮助我们突破稠密 Transformer 的缩放上限。

9.2.1 编码器-解码器

首先，回顾使用编码器-解码器框架的序列到序列任务：

$\text{input } x \quad\Rightarrow\quad \text{output } y$

示例（开放问答）：

• 输入 $x$：What is the capital of Canada?
• 输出 $y$：Ottawa

回想一下，BART 和 T5 是编码器-解码器模型的代表：

$p(y \mid x)$

其使用去噪目标函数进行训练。例如：

• 输入 $x$：Thank you $<X>$ me to your party $<Y>$ week.
• 输出 $y$：$<X>$ for inviting $<Y>$ last

9.2.2 检索方法

假设我们有一个存储库 $S$，它是一组序列（通常是文档或段落）的集合。

$S = \{ \text{Why is the...}, \text{Thanks for}, ..., \text{The quick...}, \text{Stanford...} \}.$

基于检索的模型直观的生成过程：

• 基于输入 $x$，检索相关序列$z$。
• 给定检索序列 $z$ 和输入 $x$，生成输出 $y$。

示例（开放问答）：

• 输入 $x$：What is the capital of Canada?
• 检索 $z$：Ottawa is the capital city of Canada.
• 输出 $y$：Ottawa

最近邻是最常用的一种检索方法：

• $S$ 是训练集。
• 检索 $(x',y') \in S$，使得 $x'$ 和 $x$ 最相似。
• 生成 $y = y'$。

9.2.3 Retrieval-augmented generation (RAG) (Lewis et al., 2020)

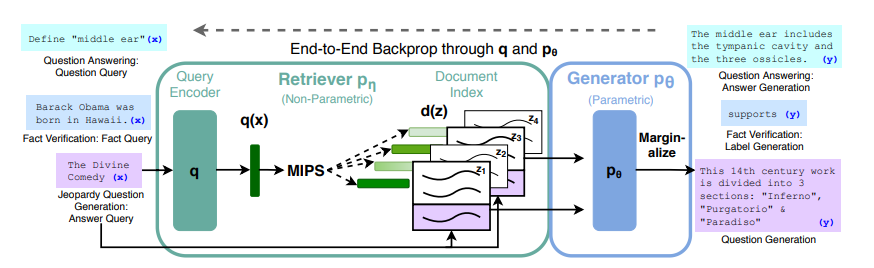
形式上，RAG 模型定义如下：

$(y \mid x) = \sum_{z \in S} \underbrace{p(z \mid x)}_\text{retriever} \underbrace{p(y \mid z, x)}_\text{generator}.$

在实践中，$\sum_{z \in S}$ 由前 $k$ 个代替（类似于为混合专家选择前 $1$ 个或 $2$ 个专家）。

• 检索器：

  Dense Passage Retrieval (DPR)** (Karpukhin et al., 2020)

  $p(z \mid x) = \frac{\exp(\text{BERT}_\text{d}(z) \cdot \text{BERT}_\text{q}(x))}{\sum_{z' \in S} \exp(\text{BERT}_\text{d}(z') \cdot \text{BERT}_\text{q}(x))}.$

  这里以用维基百科文章的标题来检索段落为例。使用 QA 数据集（如 NaturalQuestions、TriviQA 等）的 query、正例、负例 $(q, p^+, p^-_1, \dots, p^-_n)$ 来训练模型：

  • 负例：随机或者使用 BM25 检索出的不包含答案的段落

  • 推理：使用 FAISS（Facebook AI 相似性搜索）

• 生成器：

  $p(y \mid z, x) = p(y \mid \text{concat}(z, x)).$

  使用 BART-large（400M参数），其中输入为检索出的段落$z$和输入 $x$。

• 训练：

  • 用 BART、DPR（用BERT初始化）初始化

  • 训练 $\text{BART}$ 和 $\text{BERT}_\text{q}$

• 实验：

  在Jeopardy问题生成任务上，输入Hemingway的检索结果：

  

  实验结果表明，优于非检索方法。

9.3 总结

• 为了扩大模型规模，需要改进稠密 Transformer。
• 混合专家和基于检索的方法相结合更有效。
• 如何设计更好的、可扩展的体系结构仍然是一个悬而未决的问题。

9.4 Reference

混合专家模型

• Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer. Noam M. Shazeer et al.. ICLR 2017. Trains 137 billion parameter model; mixture of experts (1000 experts) applied convolutionally between LSTM layers.
• GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding. Dmitry Lepikhin et al.. ICLR 2020. Trains Transformer for neural machine translation (100 languages) with 600 billion parameters. Use top-2 experts.
• Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity. W. Fedus et al.. 2021. Trains language model, 4x speedup over T5-XXL (13 billion parameters). Use top-1 expert.
• GLaM: Efficient Scaling of Language Models with Mixture-of-Experts. Nan Du et al.. 2021. Trains 1.2 trillion parameter model, 64 experts. Use top-2 experts. Also creates new dataset.
• BASE Layers: Simplifying Training of Large, Sparse Models. M. Lewis et al.. ICML 2021. Solve optimization problem for token-to-expert allocation to balance allocation. Trains 110 billion parameter model.
• Efficient Large Scale Language Modeling with Mixtures of Experts. Mikel Artetxe et al.. 2021. Trains 1.1 trillion parameter models. Use top-2 experts (512 experts).
• Towards Crowdsourced Training of Large Neural Networks using Decentralized Mixture-of-Experts. Max Ryabinin, Anton I. Gusev. NeurIPS 2020.
• Distributed Deep Learning in Open Collaborations. Michael Diskin et al.. 2021.
• Dense-to-Sparse Gate for Mixture-of-Experts. Xiaonan Nie et al.. 2021.

基于检索的模型

• REALM: Retrieval-Augmented Language Model Pre-Training. Kelvin Guu et al.. 2020. Introduces REALM.
• Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks. Patrick Lewis et al.. NeurIPS 2020. Introduces RAG.
• Improving language models by retrieving from trillions of tokens. Sebastian Borgeaud et al.. 2021. Introduces RETRO.