0%

Large-lm-6-Training

Posted on In ,
Symbols count in article: 8.9k Reading time ≈ 8 mins.

7. 模型训练

上一章讨论了大语言模型 Transformer 的模型结构，本章节将讨论如何训练大语言模型，主要包含 目标函数 和 优化算法 两部分。

7.1 目标函数

我们研究三类语言模型的目标函数：

  1. 只包含解码器（Decoder-only）的模型（例如，GPT-3）：计算单向上下文嵌入（contextual embeddings），一次生成一个token
  2. 只包含编码器（Encoder-only）的模型（例如，BERT）：计算双向上下文嵌入
  3. 编码器解码器（Encoder-decoder）模型（例如，T5）：编码输入，解码输出

我们可以使用任何模型将 token 序列映射到上下文嵌入中：

\[ \phi : V^L \to \mathbb{R}^{d \times L}. \]

\[ \left[\text{the}, \text{mouse}, \text{ate}, \text{the}, \text{cheese}\right] \stackrel{\phi}{\Rightarrow} \left[\binom{1}{0.1}, \binom{0}{1}, \binom{1}{1}, \binom{1}{-0.1}, \binom{0}{-1} \right]. \]

7.1.1 Decode-only 模型

在自回归语言模型中，我们定义了一个条件分布： \[ p(x_i \mid x_{1:i-1}). \] 其定义如下：

  • 将 \(x_{1:i-1}\) 映射到上下文嵌入 \(\phi(x_{1:i-1})\)。
  • 应用嵌入矩阵 \(E \in \R^{V \times d}\) 来获得每个 token 的得分 \(E \phi(x_{1:i-1})_{i-1}\)。
  • 对其进行指数化和归一化，得到预测 \(x_i\) 的分布。

简洁地： \[ p(x_{i+1} \mid x_{1:i}) = softmax(E \phi(x_{1:i})_i). \] 设 \(\theta\) 是大语言模型的所有参数，\(D\) 是由一组序列组成的训练数据。然后，借助最大似然原理，可以定义以下负对数似然目标函数： \[ O(\theta) = \sum_{x \in D} - \log p_\theta(x) = \sum_{x \in D} \sum_{i=1}^L -\log p_\theta(x_i \mid x_{1:i-1}). \]

7.1.2 Encoder-only 模型

7.1.2.1 BERT 模型

此处我们介绍 BERT 的目标函数，它包含两个部分：

  • 掩码语言模型（Masked language modeling）
  • 下一句预测（Next sentence prediction）

以自然语言推理（预测隐含、矛盾或中性）任务中的序列为例： \[ x_{1:L} = [\text{[CLS]}, \text{all}, \text{animals}, \text{breathe}, \text{[SEP]}, \text{cats}, \text{breathe}]. \] 其中有两个特殊的token：

  • \(\text{[CLS]}\)：包含用于驱动分类任务的嵌入
  • \(\text{[SEP]}\)：用于告诉模型第一个序列（例如，前提）与第二个序列（例如，假设）的位置。

\(\text{SentenceEmbedding}(x_{1:L})\) 根据序列返回以下两个矢量之一

  • 对于\(\text{[SEP]}\)左边的，返回 \(e_A \in \mathbb{R}^d\)
  • 对于\(\text{[SEP]}\)右边的，返回 \(e_B \in \mathbb{R}^d\)

Note：BERT-large 有 \(n_\text{heads} = 16\) 个注意头，并且 \(d_\text{model} = 1024\)，总共355M 个参数。

7.1.2.2 掩码语言模型

掩码语言模型的基本思想是通过 加噪 然后预测来进行训练：

\[ [\text{the}, \text{[MASK]}, \text{ate}, \text{[MASK]}, \text{cheese}] \Rightarrow [\text{the}, \text{mouse}, \text{ate}, \text{the}, \text{cheese}]. \]

更普遍地说，我们可以将其视为类似于 去噪自动编码器，其中我们映射有噪声/不完整版本 \(\tilde x_{1:L}\)，并尝试重建原始 \(x_{1:L}\)。

\[ \tilde x_{1:L} \Rightarrow x_{1:L}. \]

建模：首先定义模型分布。给定输入 \(\tilde x_{1:L}\) 及其上下文嵌入，模型独立地预测每个 token： \[ p(x_i | \tilde x_{1:L}) = \text{softmax}(E \phi(\tilde x_{1:L})_i). \]

掩码：定义一个（随机）噪声函数 \(A(\tilde x_{1:L} \mid x_{1:L})\)： \[ \underbrace{x_{1:L}}_\text{original} \stackrel{A}{\Rightarrow} \underbrace{\tilde x_{1:L}}_\text{noised}. \]

其中，\(A\) 的定义如下：

  • 假设 \(I \subset \{1, \dots, L\}\) 代表所有位置中随机的 \(15\%\)。
  • 对于每个 \(i \in I\)：
    • 以 0.8 的概率，\(\tilde x_i \leftarrow \text{[MASK]}\)
    • 以 0.1 的概率，\(\tilde x_i \leftarrow x_i\)
    • 以 0.1 的概率，\(\tilde x_i \leftarrow \text{random word from } \mathcal{V}\)

减少分布偏移： 如果我们总是使用 \(\text{[MASK]}\) 来替换 \(I\) 中选定的 token，则：

  • 在训练期间，输入到 BERT 的都是带 \(\text{[MASK]}\) 的序列。
  • 而在测试时，我们会输入没有 \(\text{[MASK]}\) 的句子，这将导致分布发生变化。一种启发式的解决方法是在 \(20\%\) 的时间内用真实单词替换。

7.1.2.3 预测下一句

由于 BERT 是在拼接好的成对句子上训练的，因下一句预测的目标是预测第二句是否跟随第一句： $$ \[\begin{align*} [\text{[CLS]}, \text{the}, \text{mouse}, \text{ate}, \text{the}, \text{cheese}, \text{[SEP]}, \text{it}, \text{was}, \text{full}] &\Rightarrow 1. \\ [\text{[CLS]}, \text{the}, \text{mouse}, \text{ate}, \text{the}, \text{cheese}, \text{[SEP]}, \text{hello}, \text{world}] &\Rightarrow 0. \end{align*}\] $$

然后使用 \(\text{[CLS]}\) 的嵌入来做二分类。

7.1.2.4 数据集

\(\mathcal{D}\) 是按如下方式构造的一组样本 \((x_{1:L}, c)\)：

  • 令 \(A\) 是语料库中的一个句子。
  • 以 0.5 的概率，\(B\) 是下一个橘子。
  • 以 0.5 的概率，\(B\) 是语料库中的一个随机句子。
  • 令 \(x_{1:L} = [\text{[CLS]}, A, \text{[SEP]}, B]\)
  • 令 \(c\) 表示 \(B\) 是否是下一句。

7.1.2.5 训练目标

BERT 的训练目标是： \[ \mathcal{O}(\theta) = \sum_{(x_{1:L},c) \in \mathcal{D}} \underbrace{\mathbb{E}_{I, \tilde x_{1:L} \sim A(\cdot \mid x_{1:L}, I)}[\sum_{i \in I} -\log p_\theta(\tilde x_i | x_{1:L})]}_\text{masked language modeling} + \underbrace{-\log p(c | \phi(x_{1:L})_1)}_\text{next sentence prediction}. \]

7.1.2.6 总结

  • BERT（以及 ELMo 和 ULMFiT）表明，一个统一的体系结构（Transformer）可以用于多个分类任务。
  • BERT 真正将 NLP 社区转变为预培训+微调的范式。
  • BERT 显示了深度双向上下文嵌入的重要性，尽管通过模型大小和微调策略可能会弥补这一点（p-tuning）。

相对于传统的 BERT 模型，RoBERTa 进行了以下改进：

  • 删除了下一句预测这一目标函数（发现它没有帮助）。
  • 使用更多数据训练（16GB文本 \(\to\) 160GB文本）。
  • 训练时间更长。

通过上述努力，RoBERTa 在各种基准上显著提高了 BERT 的准确性，如在 SQuAD 上： \(81.8 \to 89.4\)。

7.1.3 Encoder-decoder 模型

任务示例（表格生成文本）： \[ [\text{name}, \text{:}, \text{Clowns}, \text{|}, \text{eatType}, \text{:}, \text{coffee}, \text{shop}] \rightarrow [\text{Clowns}, \text{is}, \text{a}, \text{coffee}, \text{shop}]. \]

7.1.3.1 BART (Bidirectional Auto-Regressive Transformers)

BART (Lewis et al. 2019) 是基于 Transformer 的编码器-解码器模型。

  • 使用与 RoBERTa 相同的编码器架构（12层，隐藏维度1024）。
  • 使用与 RoBERTa 相同的数据进行训练（160GB 文本）。

BART 使用了以下变换 \(A(\tilde x_{1:L} \mid x_{1:L})\)：

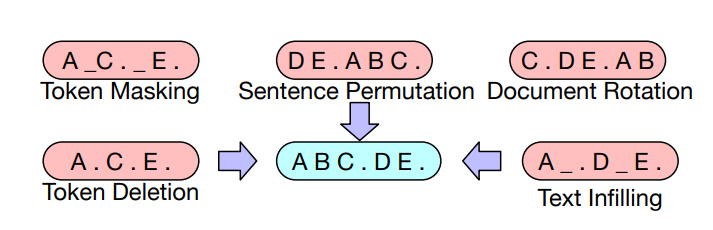
基于 BERT 的实验，最终模型进行以下了变换：

  • 掩码文档中 \(30\%\) 的 token
  • 将所有子句打乱

最后，通过微调，BART 在分类和生成任务上都展示了强大的效果。

7.1.3.2 T5 (Text-to-Text Transfer Transformer)

T5 (Raffel et al., 2020) 是另一种基于 Transformer 的编码器-解码器模型。

预训练任务： 给定一段文本，在随机位置将其分割为输入和输出： \[ [\text{the}, \text{mouse}] \Rightarrow [\text{ate}, \text{the}, \text{cheese}]. \]

论文尝试了许多不同的无监督目标：

并发现 “i.i.d. noise, replace spans” 效果最好（尽管许多目标相似）。论文还将所有经典的 NLP 任务放在一个统一的框架中，称为 Text-to-Text 任务：

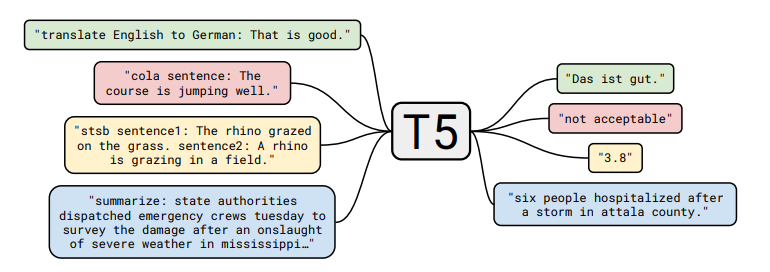
以分类任务任务为例，不同模型的差异如下：

  • BERT 使用 \(\text{[CLS]}\) 的嵌入来预测。
  • T5、GPT-2、GPT-3 等（生成模型）将分类任务转换成自然语言生成。

注意：

  • 论文对整个 pipline 的许多方面（数据集、模型大小、训练目标等）进行了深入研究。
  • 基于这些见解，他们训练了一个 11B 的模型。

7.2 优化算法

现在，我们将注意力转向如何优化目标函数。

为了简单起见，让我们以自回归语言模型为例： \[ O(\theta) = \sum_{x \in D} -\log p_\theta(x). \]

7.2.1 随机梯度下降（SGD）

最简单的优化算法是用小批量进行随机梯度下降，该算法的步骤如下：

  • 初始化参数 \(\theta_0\)

  • 重复以下步骤：

    • 采样小批量 \(B_t \subset D\)
    • 根据梯度更新参数：

    \[ \theta_t \leftarrow \theta_{t-1} - \eta \frac{1}{|B_t|} \sum_{x \in B_t} \nabla_\theta (-\log p_\theta(x)). \]

关键目标是：

  1. 希望参数 \(\theta\) 可以快速收敛
  2. 希望优化在数值上是稳定的
  3. 希望内存高效（尤其是对于大模型）

这些点往往相互矛盾（例如，通过低精度训练，可以实现快速收敛、减少内存占用，但是会导致训练不稳定）

因此，可以从几个层次来进行优化：

  1. 针对经典优化：二阶方法、约束优化等。
  2. 针对机器学习：随机方法、隐式正则化+早停法
  3. 针对深度学习：初始化、归一化（更改模型架构）
  4. 针对大语言模型：由于稳定性问题，学习率和一些直觉（例如，二阶方法）仍然有用，但要使大语言模型有效训练，还需要克服许多其他独特的挑战。不幸的是，其中大部分内容都是特别的，人们对此了解甚少。

7.2.2 Adam (adaptive moment estimation)

Adam 算法拥有以下两个创新：

  1. 引入动量（继续朝同一方向移动）。
  2. 参数 \(\theta_0\) 的每个维度都有一个自适应（不同）的步长（受二阶方法启发）。

它的步骤如下：

  • 初始化参数 \(\theta_0\)

  • 初始化动量 \(m_0, v_0 \leftarrow 0\)

  • 重复以下步骤：

    • 采样小批量 \(B_t \subset D\)

    • 按照如下步骤更新参数：

      • 计算梯度

      \[ g_t \leftarrow \frac{1}{|B_t|} \sum_{x \in B_t} \nabla_\theta (-\log p_\theta(x)). \]

      • 更新一阶、二阶动量

      \[ m_t \leftarrow \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ v_t \leftarrow \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 \]

      • 对偏差进行修正

      \[ \hat m_t \leftarrow m_t / (1 - \beta_1^t) \\ \hat v_t \leftarrow v_t / (1 - \beta_2^t) \]

      • 更新参数

      \[ \theta_t \leftarrow \theta_{t-1} - \eta \, \hat m_t / (\sqrt{\hat v_t} + \epsilon). \]

存储占用分析：

Adam 将存储从 2 倍的模型参数（\(\theta_t,g_t\)）增加到了4倍（\(\theta_t,g_t,m_t,v_t\)）。

7.2.3 AdaFactor

AdaFactor 是一种为减少存储占用的优化算法。它有如下特点：

  • 它不储存 \(m_t,v_t\) 这样的 \(O(m \times n)\) 矩阵，而是存储行和列的和 \(O(m + n)\) 并重构矩阵
  • 去除动量
  • 它被用来训练 T5
  • AdaFactor 可能使训练变得困难（see Twitter thread and blog post）

7.2.4 混合精度训练

混合精度训练 是另一种减少存储的方法

  • 通常来说，默认的精度是：FP32（32位浮点）
  • 其他可选精度：FP16（16位浮点），但问题是任何小于 \(2^{-24}\) 的值都会变为 0。
  • 解决方案：将主权重存储在 FP32 中，并在 FP16 中执行其他所有操作。
  • 损失缩放：按比例放大损失，以避免梯度数值太小。
  • 结果：存储减少了一半。

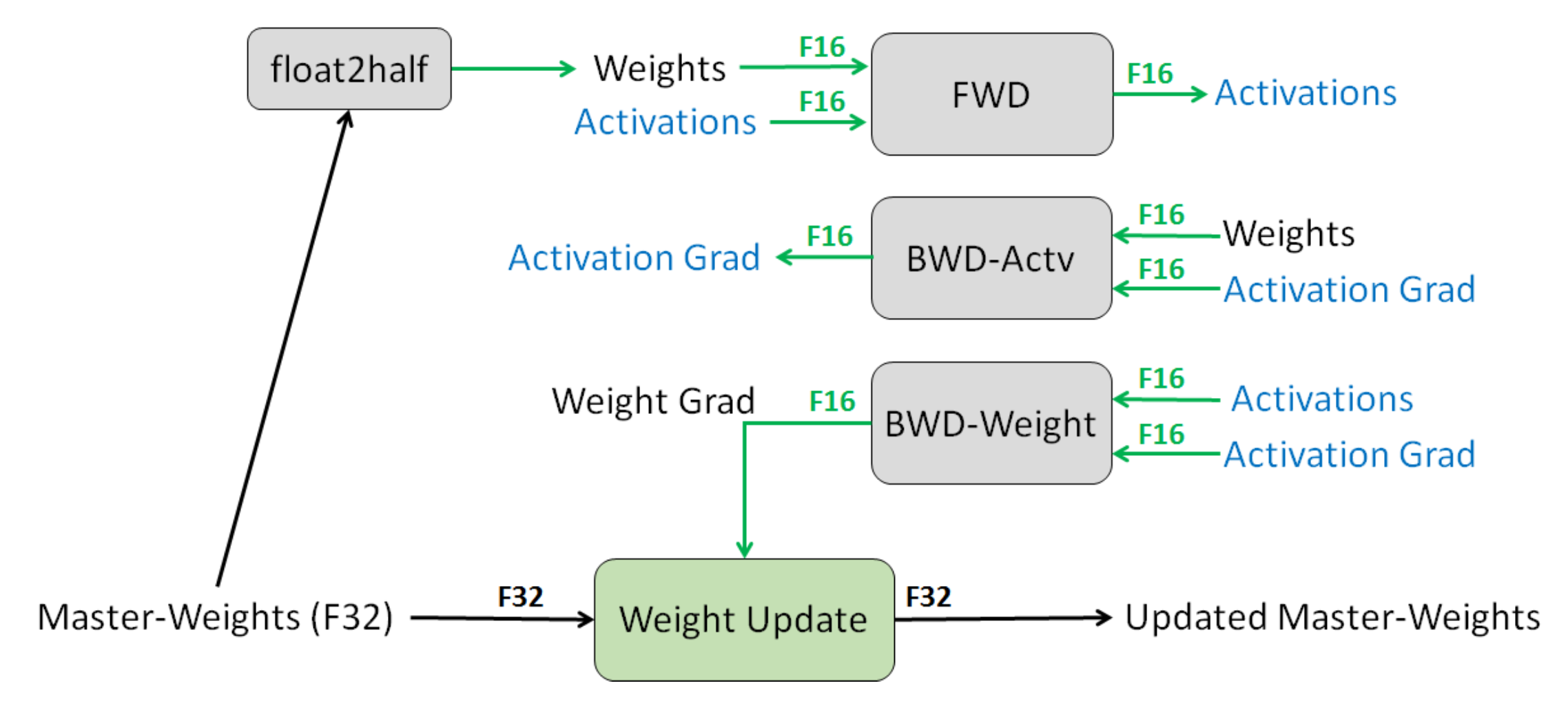
7.2.5 学习率

  • 通常情况下，学习率会随着时间的推移而衰减。
  • 对于 Transformer 模型，我们实际上需要通过预热（warmup）提高学习率。
  • Huang et al. (2020) 表明，一个潜在的原因是防止层归一化的梯度消失，导致使用 Adam优化器训练时不稳定。

7.2.6 初始化

  • 给定矩阵 \(W \in \mathbb{R}^{m \times n}\)，标准初始化（即，xavier 初始化）为 \(W_{ij} \sim N(0, 1/n)\)。
  • GPT-2 和 GPT-3 通过额外的 \(\frac{1}{\sqrt{N}}\) 缩放权重，其中 \(N\) 是残差层的数量。
  • T5将注意力矩阵增加一个\(\frac{1}{\sqrt{d}}\)（代码）。

以 GPT-3 为例，使用的参数如下：

  • Adam参数：\(\beta_1 = 0.9, \beta_2 = 0.95, \epsilon = 10^{-8}\)
  • 批量小：320万个token（约 1500 个序列）
  • 使用梯度剪裁（\(g_t \leftarrow g_t / \min(1, \|g\|_2)\)）
  • 线性学习率预热（前3.75亿个token）
  • 余弦学习率 衰减到 \(10\%\)
  • 逐渐增加批大小
  • 权重衰减设为 0.1

7.3 Reference

8. 分布式训练

近年来，深度学习被广泛应用到各个领域，包括计算机视觉、语言理解、语音识别、广告推荐等。不同的领域下的模型规模越来越大，比如 GPT-3 模型的参数量达到 1750 亿。即使用 1024 张 80 GB 的 A100，那么完整训练 GPT-3 的时长都需要1个月。

模型规模的扩大，对硬件（算力、内存）的发展提出要求。然而，因为 内存墙 的存在，单一设备的算力及容量，受限于物理定律，持续提高芯片的集成越来越困难，难以跟上模型扩大的需求。为了解决算力增速不足的问题，人们考虑用多节点集群进行分布式训练，以提升算力。因此分布式训练势在必行，也成为近些年来的流行方案。

8.1 常见的并行策略

简单的机器堆叠并不一定会带来算力的增长。因为神经网络的训练不仅需要多个设备进行计算，还涉及到设备之间的数据传输，只有协调好集群中的计算与通信，才能做高效的分布式训练。

我们将以矩阵乘法的例子，解释数据并行、模型并行的区别。先了解以下逻辑上的矩阵乘法例子：

假设神经网络中某一层是做矩阵乘法，其中的输入 \(x\) 的形状为 \(4\times5\)，模型参数 \(w\) 的形状为\(5\times8\)，那么，矩阵乘法输出形状为 \(4\times8\)。示意图如下：

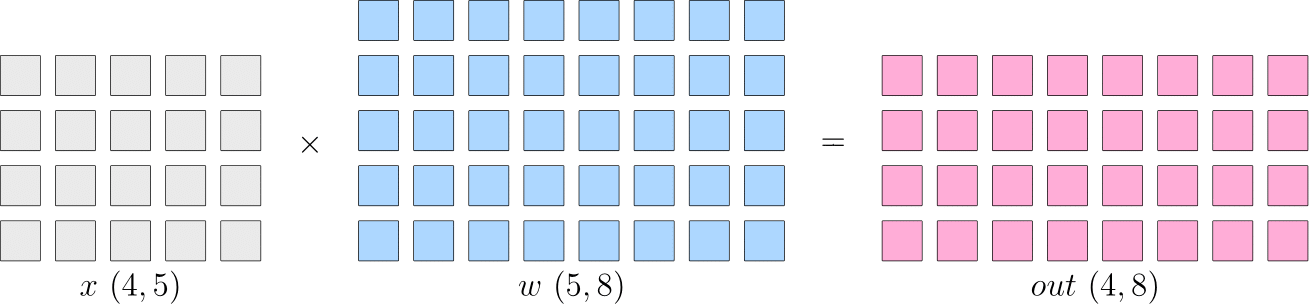
单机单卡的训练中，以上矩阵乘法，先计算得到 \(out\)，并将 \(out\) 传递给下一层，并最终计算得到\(loss\)，然后在反向传播过程中，得到 \(\frac{\partial loss}{\partial w}\)，用于更新 \(w\)。

分布式训练中，依据是切分 \(x\) 还是 \(w\) 的不同，分为“数据并行”和“模型并行”策略。接下来，我们介绍常见的并行策略。

8.2.1 数据并行

数据并行，就是将数据 \(x\) 进行切分，而每个设备上的模型 \(w\) 是相同的。如下图所示，\(x\) 被按照第 \(0\) 维度平均切分到 \(2\) 个设备上，两个设备上都有完整的 \(w\)。

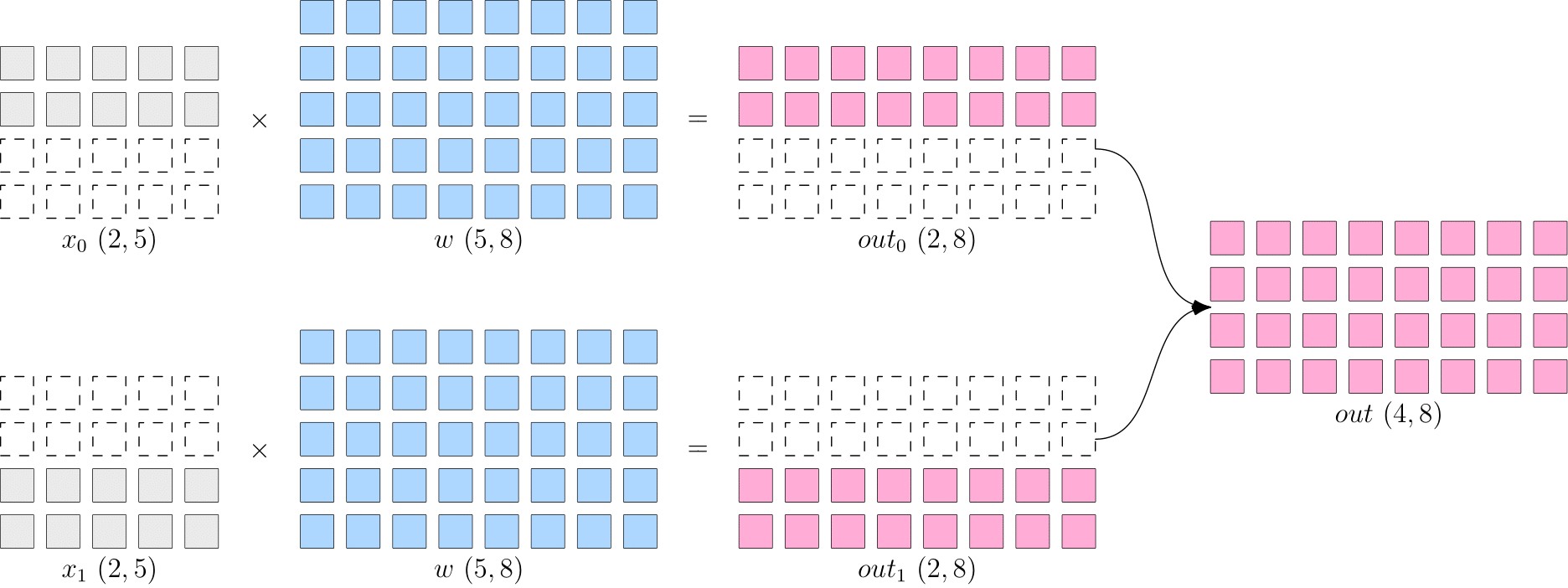
这样，在两台设备上，分别得到的输出，都只是逻辑上输出的一半（形状为 \(2\times8\)），将两个设备上的输出拼接到一起，才能得到逻辑上完整的输出。

Note：因为数据被分发到了 \(2\) 个设备上，因此反向传播过程，各自设备上得到的 \(\frac{\partial loss}{\partial w}\) 会不一样，如果直接使用各个设备上的梯度更新各自的模型，会造成 \(2\) 个设备上的模型不一致，训练就失去了意义（到底用哪个模型好呢？）。

因此，数据并行策略下，在反向传播过程中，需要对各个设备上的梯度进行 AllReduce，以确保各个设备上的模型始终保持一致。

  • 当数据集较大，模型较小时，由于反向过程中为同步梯度产生的通信代价较小，此时选择数据并行一般比较有优势，常见的视觉分类模型，如 ResNet50，比较适合采用数据并行。

8.2.2 模型并行

当神经网络非常巨大，数据并行同步梯度的代价就会很大，甚至网络可能巨大到无法存放到单一计算设备中，这时候，可以采用模型并行策略解决问题。

模型并行 指每个设备上的数据是完整的、一致的，而模型 \(w\) 被切分到了各个设备上，每个设备只拥有模型的一部分，所有计算设备上的模型拼在一起，才是完整的模型。 如下图所示，\(w\) 被按照第 \(1\) 维度平均切分到 \(2\) 个设备上，两个设备上都有完整的 \(x\)。两个设备上的输出也需要通过拼接才能得到逻辑上的输出。

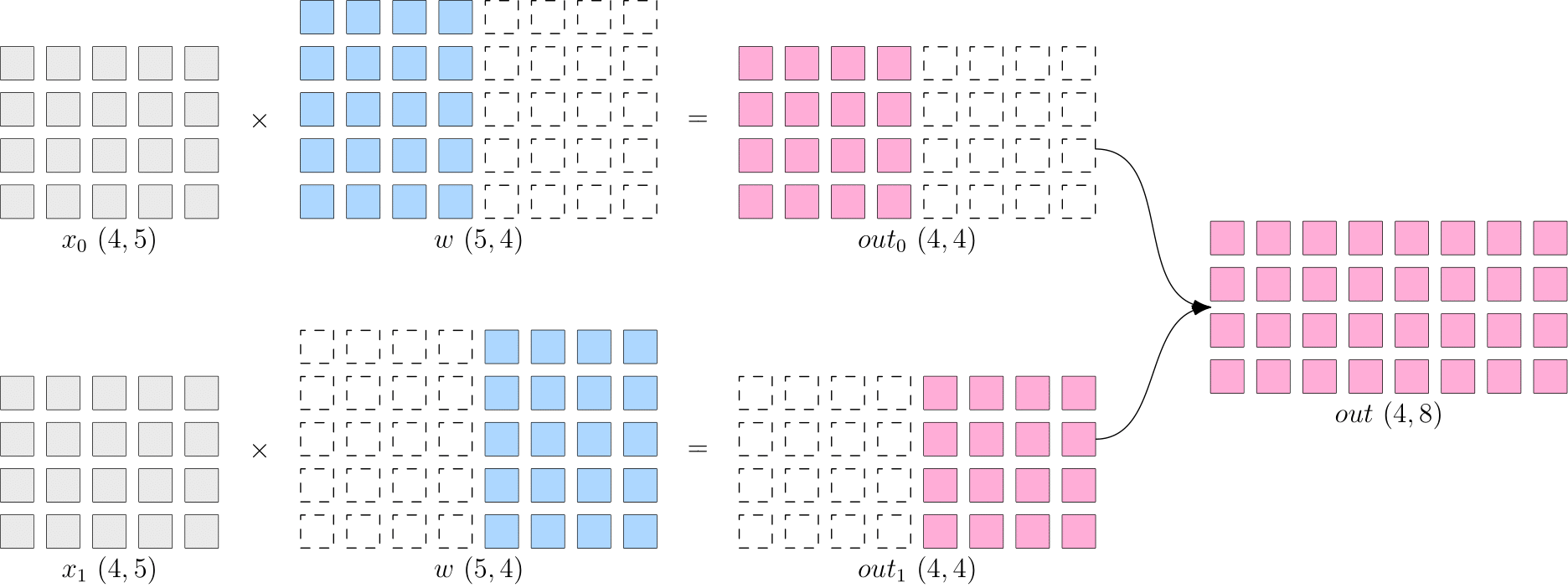
  • 优点：省去了多个设备之间的梯度 AllReduce；
  • 缺点：由于每个设备都需要完整的数据输入，因此，数据会在多个设备之间进行广播，产生通信代价。

比如，上图中的最终得到的 \(out~(4\times8)\) ，如果它作为下一层网络的输入，那么它就需要被广播发送到两个设备上。语言模型，如 BERT，常采用模型并行。

8.2.3 流水并行

当神经网络过于巨大，无法在一个设备上存放时，除了上述的模型并行的策略外，还可以选择流水并行。

流水并行 指将网络切为多个阶段，并分发到不同的计算设备上，各个计算设备之间以“接力”的方式完成训练。

如下图，展示了一个逻辑上的 4 层网络 (T1至T4) 是如何做流水并行的。4 层网络被切分到 2 个计算设备上，其中 GPU0 上进行 T1 与 T2 的运算，GPU1 上进行 T3 与 T4 的计算。GPU0 上完成前两层的计算后，它的输出被当作 GPU1 的输入，继续进行后两层的计算。

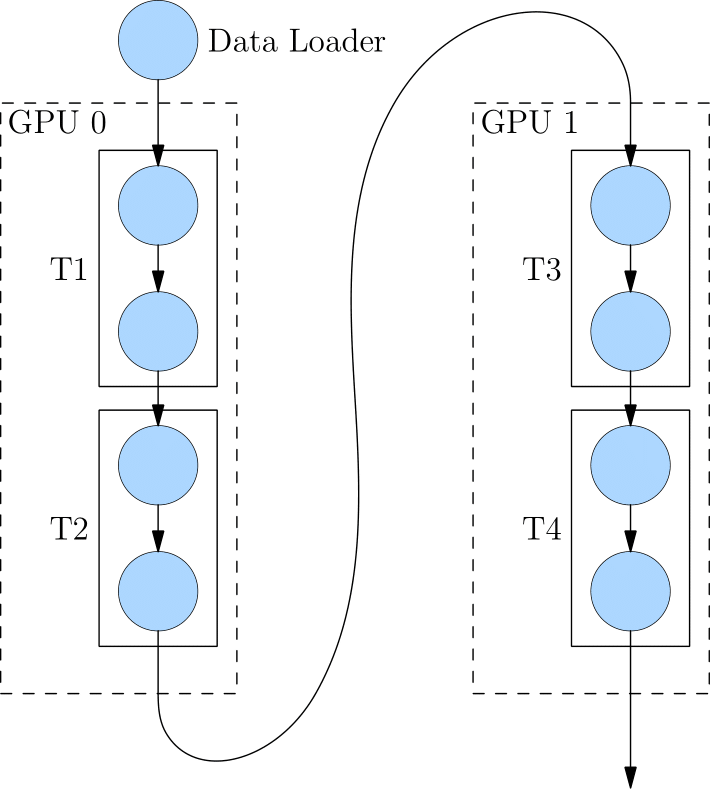
8.2.4 混合并行

网络的训练中，也可以将多种并行策略混用，以 GPT-3 为例，以下是它训练时的设备并行方案： 它首先被分为 64 个阶段，进行流水并行。每个阶段都运行在 6 台 DGX-A100 主机上。在6台主机之间，进行的是数据并行训练；每台主机有 8 张 GPU 显卡，同一台机器上的8张 GPU 显卡之间是进行模型并行训练。

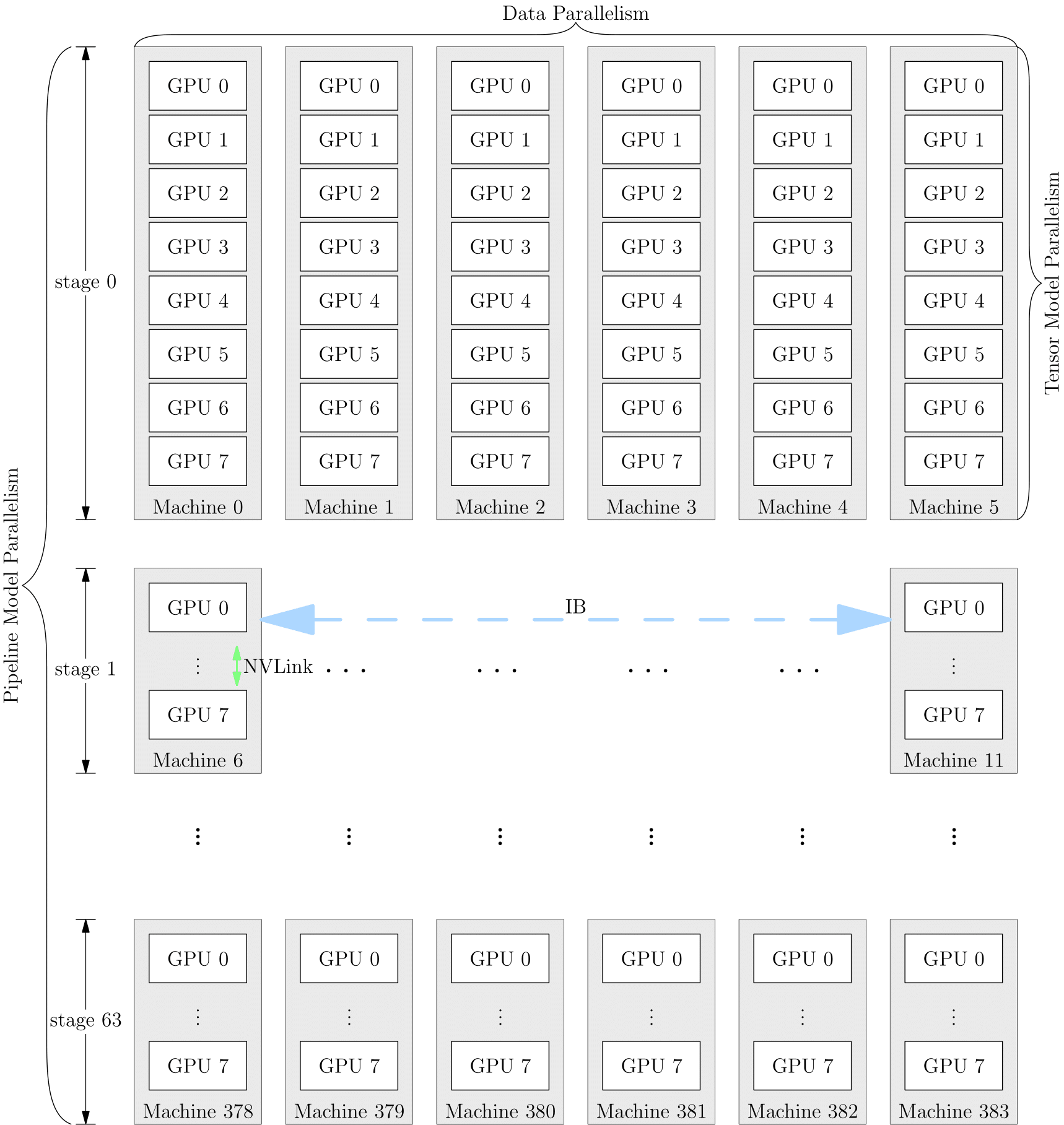
并行策略的选择影响着训练效率，框架对并行训练的接口支持程度，决定了算法工程师的开发效率。

8.3 Reference

-------------This blog is over! Thanks for your reading-------------