0. Preface
Most folks are as happy as they make up their minds to be.
— Abraham Lincoln
本系列博文是 DataWhale 社区 2023年 3月《动手学深度学习(Pytorch)》组队学习活动的笔记,本篇为系列笔记的第三篇—— 多层感知机。
本文是学习李沐老师 B 站视频教程 动手学深度学习 PyTorch版 所记录的笔记。主要使用 Obsidian 软件并借助插件 Meida extended 插件,在 markdown 文件中生成时间戳,可以在后期温习笔记时,方便地定位到原视频所在位置。
原教程视频如下:
PDF 版本笔记见:D2L Note Chapter 3
本次活动面向的人员:
- 有Python基础
- 有高数,线代,概率论基础
- 本科大二左右,或者研一
学习资源整合
3 多层感知机
3 多层感知机
3.1 多层感知机
#ob-media, #mlp
3.1.1 感知机
3.1.1.1 定义
从现在的观点来看,感知机实际上就是神经网络中的一个神经单元:
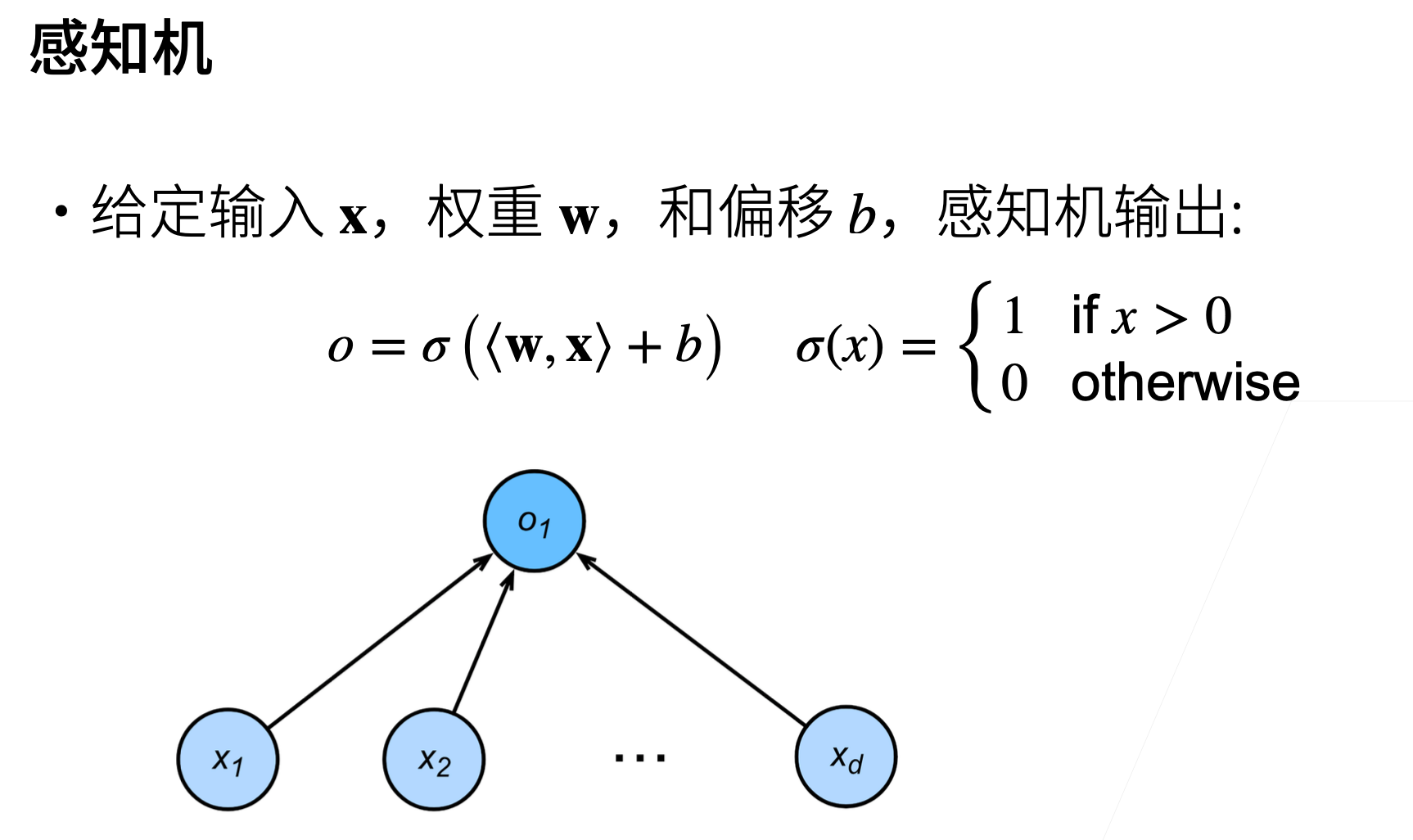 - 给定输入 $x$,权重 $w$ 和偏移 $b$,感知机的输出为:
- 给定输入 $x$,权重 $w$ 和偏移 $b$,感知机的输出为:
$$
o=\sigma(\langle\mathbf{w}, \mathbf{x}\rangle+b) \quad \sigma(x)=\left\{\begin{array}{ll}
1 & \text { if } x>0 \\
0 & \text { otherwise }
\end{array}\right.
$$
感知机能解决二分类问题,但与线性回归和 softmax 回归有所区别:
- 线性回归与
softmax回归的输出均为实数 softmax回归的输出同时还满足概率公理。
3.1.1.2 训练
训练感知机的伪代码如下:
1 | <font face="Times new roman" > |
可以看出这等价于使用如下损失函数的随机梯度下降(batch_size=1):
当预测错误时,偏导数为
注:此处为了方便计算,将偏置项 归入 中的最后一维,并在特征 中相应的最后一维加入常数 1。
3.1.1.3 收敛定理
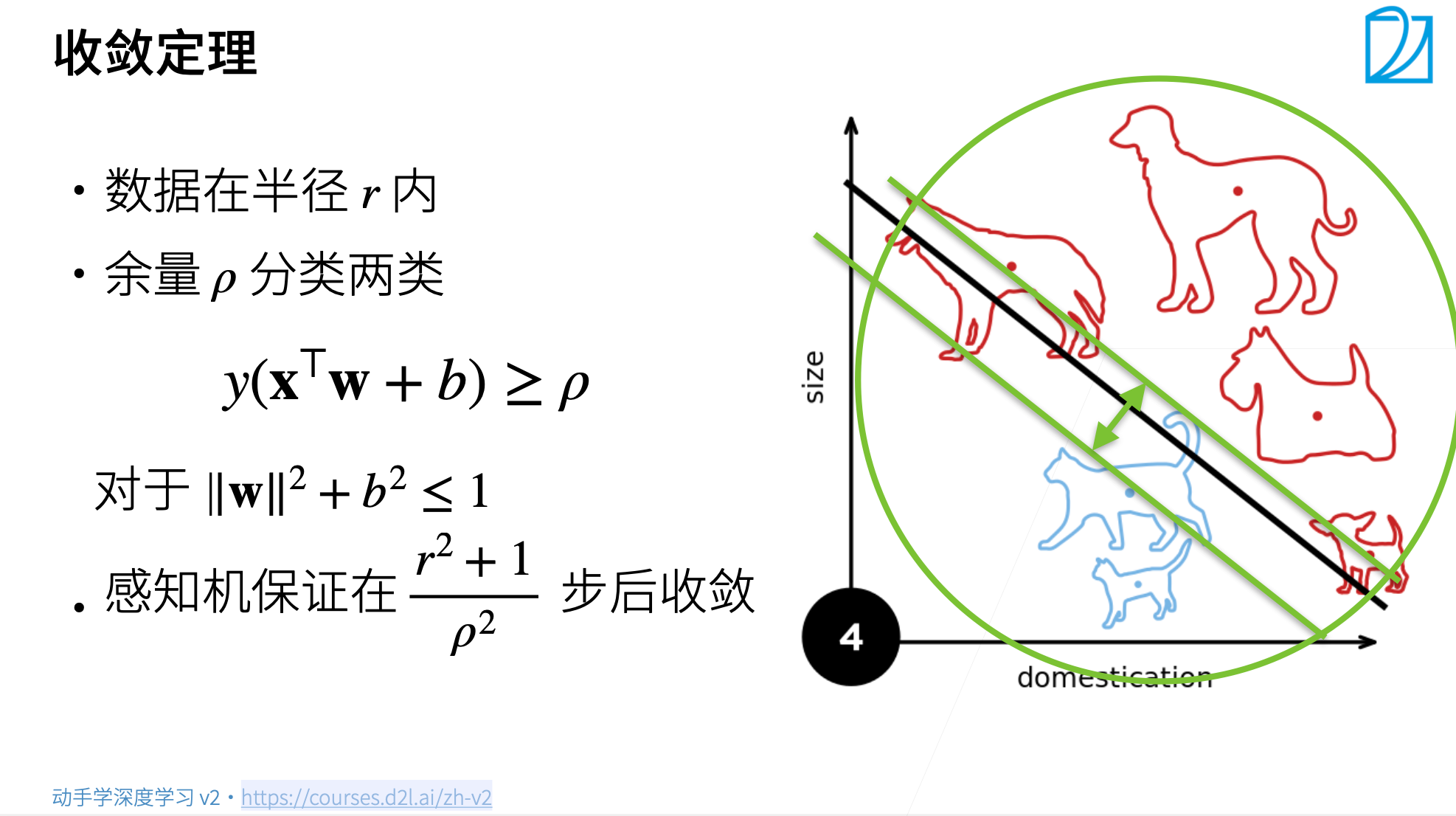 设数据在特征空间能被半径为 $r$ 的圆(球)覆盖,并且分类时有余量(即 $\sigma$ 函数的输入不会取使输出模棱两可的值) $y(\bf x^T\bf w)\geq \rho$ ,若初始参数满足 $\|\bf w\|^2+b^2 \leq 1$ ,则感知机保证在 $\bf{r^2+1}{\rho ^2}$ 步内收敛。
设数据在特征空间能被半径为 $r$ 的圆(球)覆盖,并且分类时有余量(即 $\sigma$ 函数的输入不会取使输出模棱两可的值) $y(\bf x^T\bf w)\geq \rho$ ,若初始参数满足 $\|\bf w\|^2+b^2 \leq 1$ ,则感知机保证在 $\bf{r^2+1}{\rho ^2}$ 步内收敛。
收敛性的证明可以查看:收敛性的证明
3.1.1.4 线性模型的缺陷
在前面的课程中我们学习了 softmax 回归,线性回归,他们有将输入向量与一个权重向量做内积再与一个偏置相加得到一个值的过程:
这个过程被称为仿射变换,它是一个带有偏置项的线性变换,它最终产生的模型被称为线性模型,线性模型的特点是只能以线性的方式对特征空间进行划分:
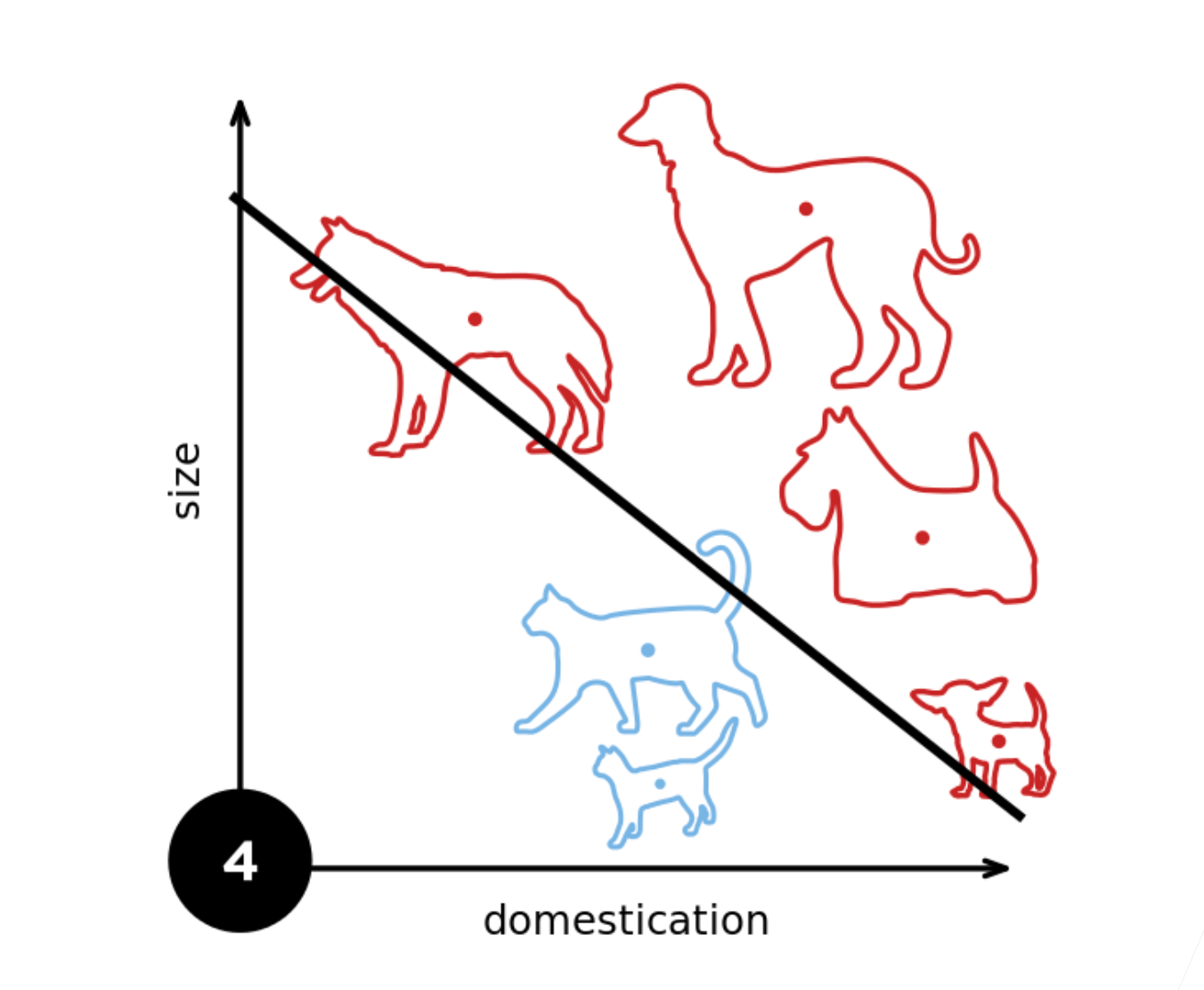
然而,这种线性划分依赖于线性假设,是非常不可靠的
线性假设意味着单调假设,这是不可靠的:
- 对于人体的体温与健康情况的建模,人体在37℃时最为健康,过小过大均有风险,然而这不是单调的
线性假设意味着特征与预测存在线性相关性,这也是不可靠的:
- 如果预测一个人偿还债务的可能性,那这个人的资产从0万元增至5万元和从100万元增至105万元对应的偿还债务的可能性的增幅肯定是不相等的,也就是不线性相关的
线性模型的评估标准是有位置依赖性的,这是不可靠的:
- 如果需要判断图片中的动物是猫还是狗,对于图片中一个像素的权重的改变永远是不可靠的,因为如果将图片翻转,它的类别不会改变,但是线性模型不具备这种性质,像素的权重将会失效
XOR 问题:
希望模型能预测出 XOR 分类(分割图片中的一三象限与二四象限):
 #### 3.1.1.5 总结
#### 3.1.1.5 总结
[!summary]+
- 感知机是一个二分类模型,是最早的
AI模型之一;- 它的求解算法等价于使用批量大小为 的梯度下降;
- 它不能你和
XOR函数,导致第一次AI寒冬。
3.1.2 多层感知机
3.1.2.1 XOR问题的多层次解决
XOR 问题的一个解决思路是分类两次:
- 先按 轴分类为
+和-; - 再按y轴分类为
+和-; - 最后将两个分类结果相乘,
+即为一三象限,-即为二四象限:
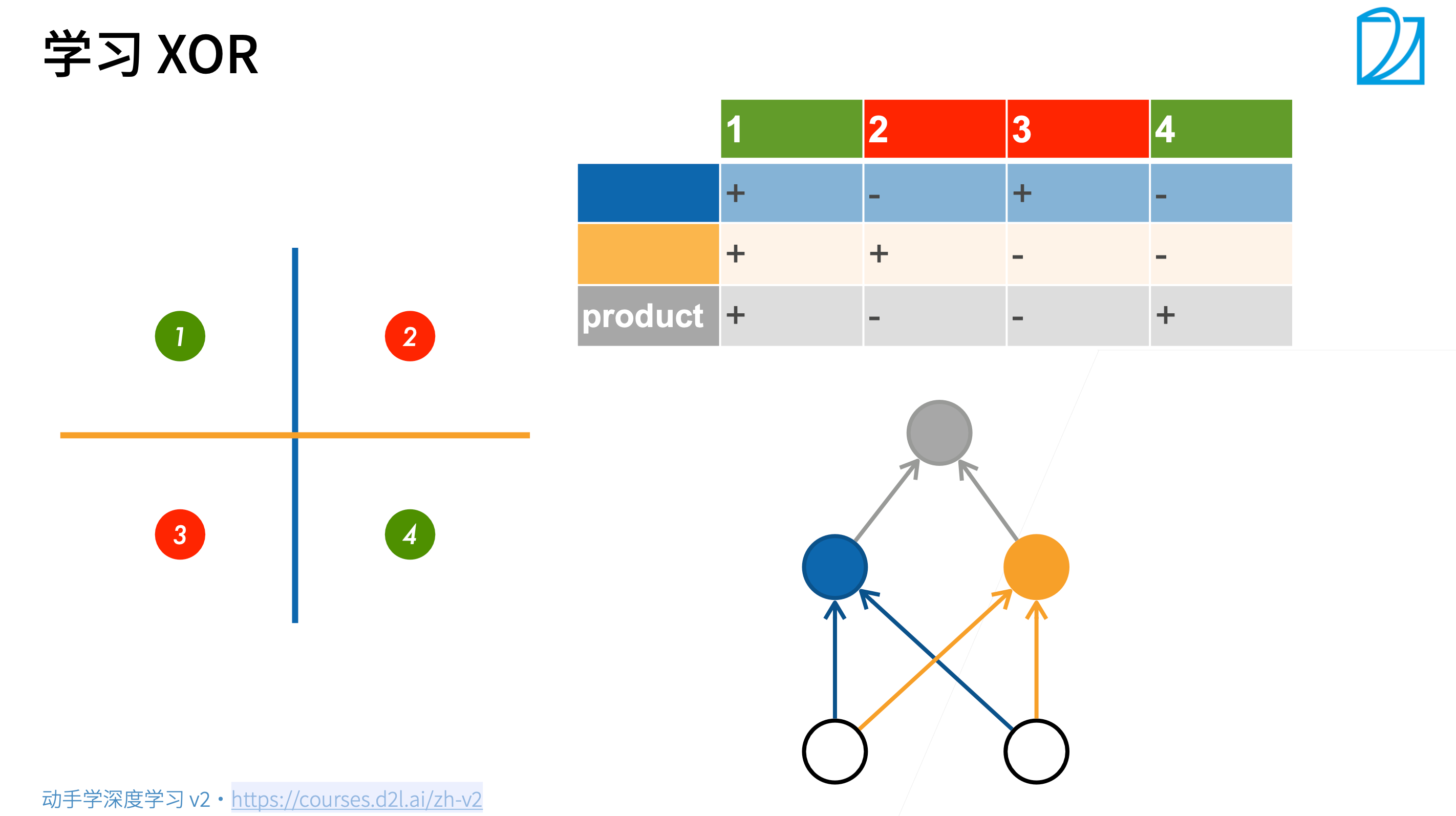 这实际上将信息进行了多层次的传递:
这实际上将信息进行了多层次的传递:
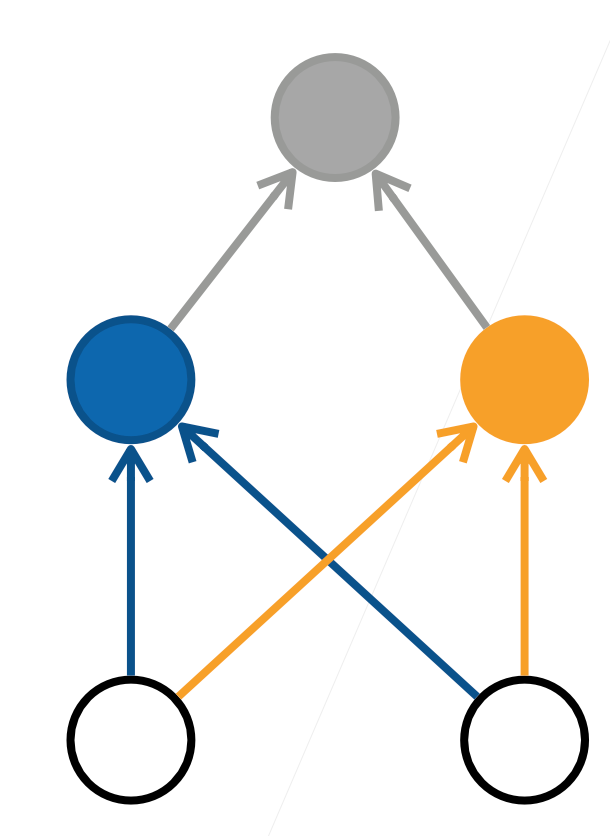 其中蓝色为按 `X` 坐标的正负进行的分类,橙色为按 `Y` 坐标的正负进行的分类,灰色为将二者信息的综合,这就实现了用多层次的线性模型对非线性进行预测。
其中蓝色为按 `X` 坐标的正负进行的分类,橙色为按 `Y` 坐标的正负进行的分类,灰色为将二者信息的综合,这就实现了用多层次的线性模型对非线性进行预测。
3.1.2.2 多层感知机
有了 XOR 问题的解决经验,可以想到如果将多个感知机堆叠起来,形成具有多个层次的结构,如下图:
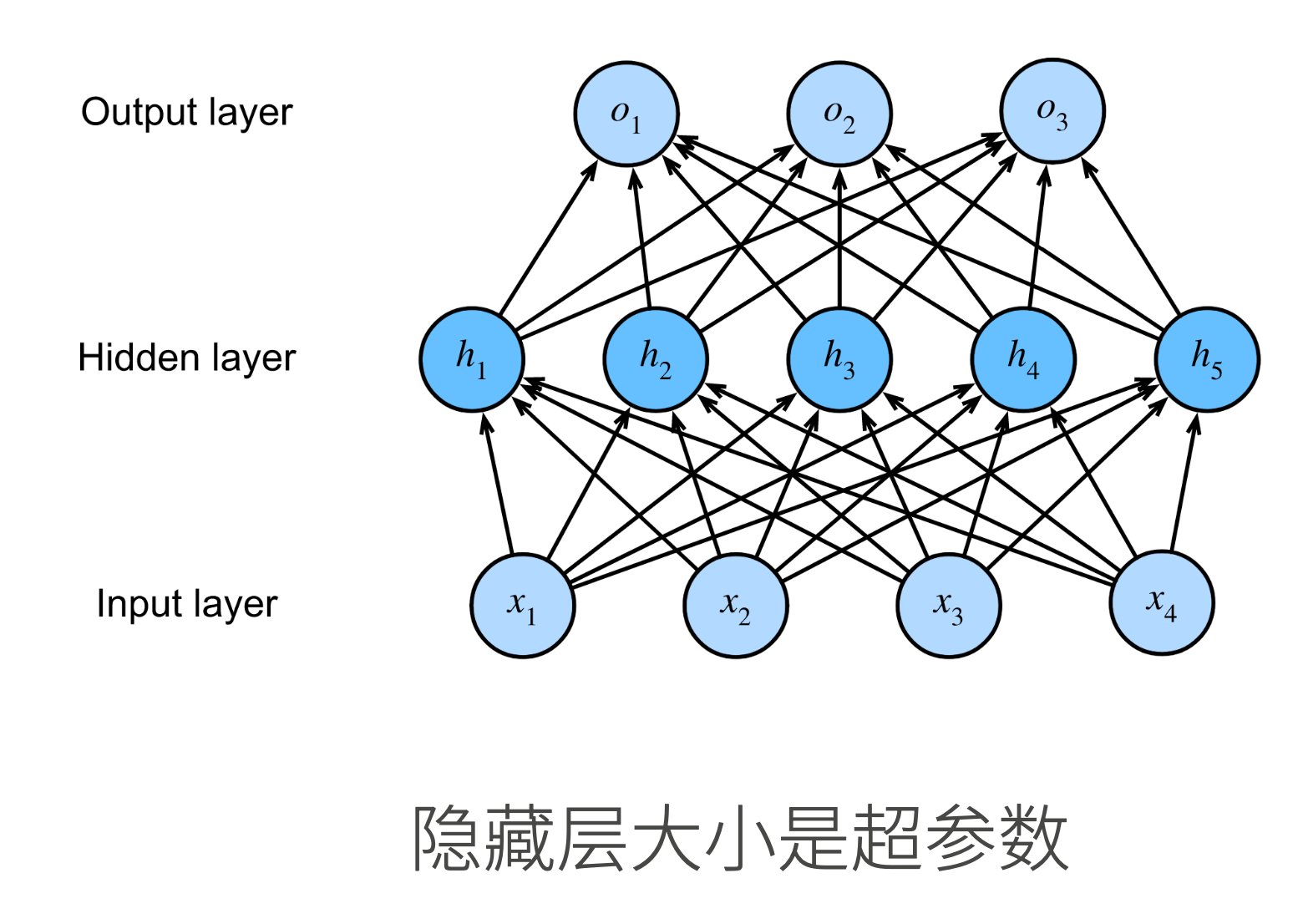 这里的模型称为 **多层感知机**:
- **输入**:$x_1,x_2,x_3,x_4$ ,$\mathbf{x} \in \mathbb{R}^n$
- **隐藏层**:由 `5` 个感知机构成,均以前一层的信息作为输入。
$$
\mathbf{h}=\sigma\left(\mathbf{W}_1 \mathbf{x}+\mathbf{b}_1\right)
$$
其中,$\mathbf{W}_1 \in \mathbb{R}^{m \times n}, \mathbf{b}_1 \in \mathbb{R}^m$,$\sigma$ 是按元素的激活函数。
- **输出层**:以前一层隐藏层的结果作为输入。
$$
o=\mathbf{w}_2^T \mathbf{h}+b_2
$$
其中,$\mathbf{w}_2 \in \mathbb{R}^m, b_2 \in \mathbb{R}$
这里的模型称为 **多层感知机**:
- **输入**:$x_1,x_2,x_3,x_4$ ,$\mathbf{x} \in \mathbb{R}^n$
- **隐藏层**:由 `5` 个感知机构成,均以前一层的信息作为输入。
$$
\mathbf{h}=\sigma\left(\mathbf{W}_1 \mathbf{x}+\mathbf{b}_1\right)
$$
其中,$\mathbf{W}_1 \in \mathbb{R}^{m \times n}, \mathbf{b}_1 \in \mathbb{R}^m$,$\sigma$ 是按元素的激活函数。
- **输出层**:以前一层隐藏层的结果作为输入。
$$
o=\mathbf{w}_2^T \mathbf{h}+b_2
$$
其中,$\mathbf{w}_2 \in \mathbb{R}^m, b_2 \in \mathbb{R}$
除了输入的信息和最后一层的感知机以外,其余的层均称为隐藏层,隐藏层的设置为模型一个重要的超参数,这里的模型有一个隐藏层。
3.1.2.3 激活函数
仅仅有线性变换是不够的,如果我们简单的将多个线性变换按层次叠加,由于线性变换的结果仍为线性变换,所以最终的结果等价于线性变换,与单个感知机并无区别,反而加大了模型,浪费了资源。
为了防止这个问题,需要对每个单元(感知机)的输出通过激活函数进行处理再交由下一层的感知机进行运算,这些激活函数就是解决非线性问题的关键。
激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活,它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。主要的激活函数有:
- Sigmoid 激活函数
Sigmoid 激活函数将输入投影到 ,是一个软的 。
目前,sigmoid 在隐藏层中已经较少使用,它在大部分时候被更简单、更容易训练的 ReLU 所取代。
导数为下面的公式:
1 | y = torch.sigmoid(x) |
Results:
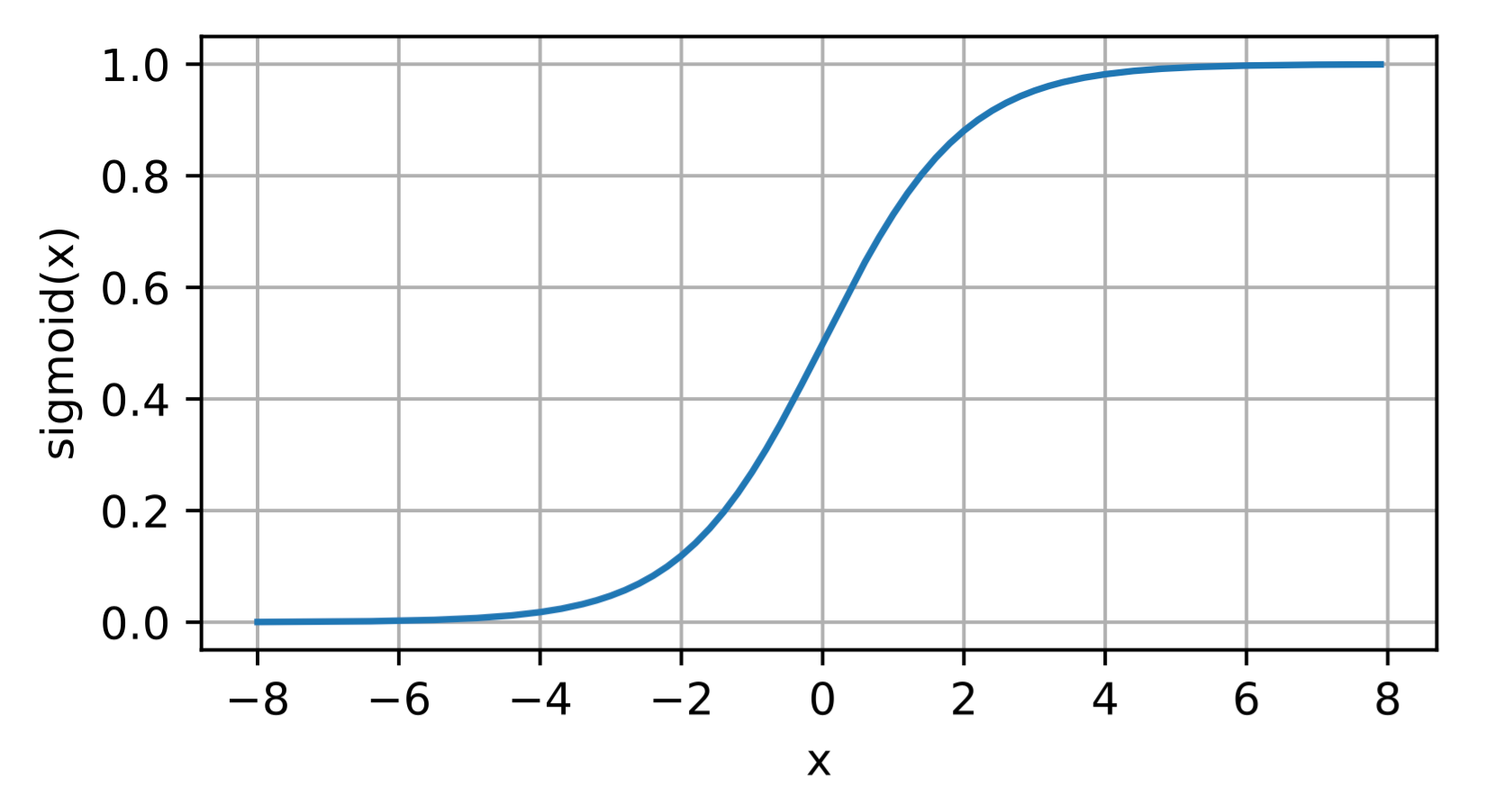 **Note**:当输入接近0时,sigmoid函数接近线性变换。
**Note**:当输入接近0时,sigmoid函数接近线性变换。
- sigmoid函数的导数:
1 | # 清除以前的梯度 |
Results:
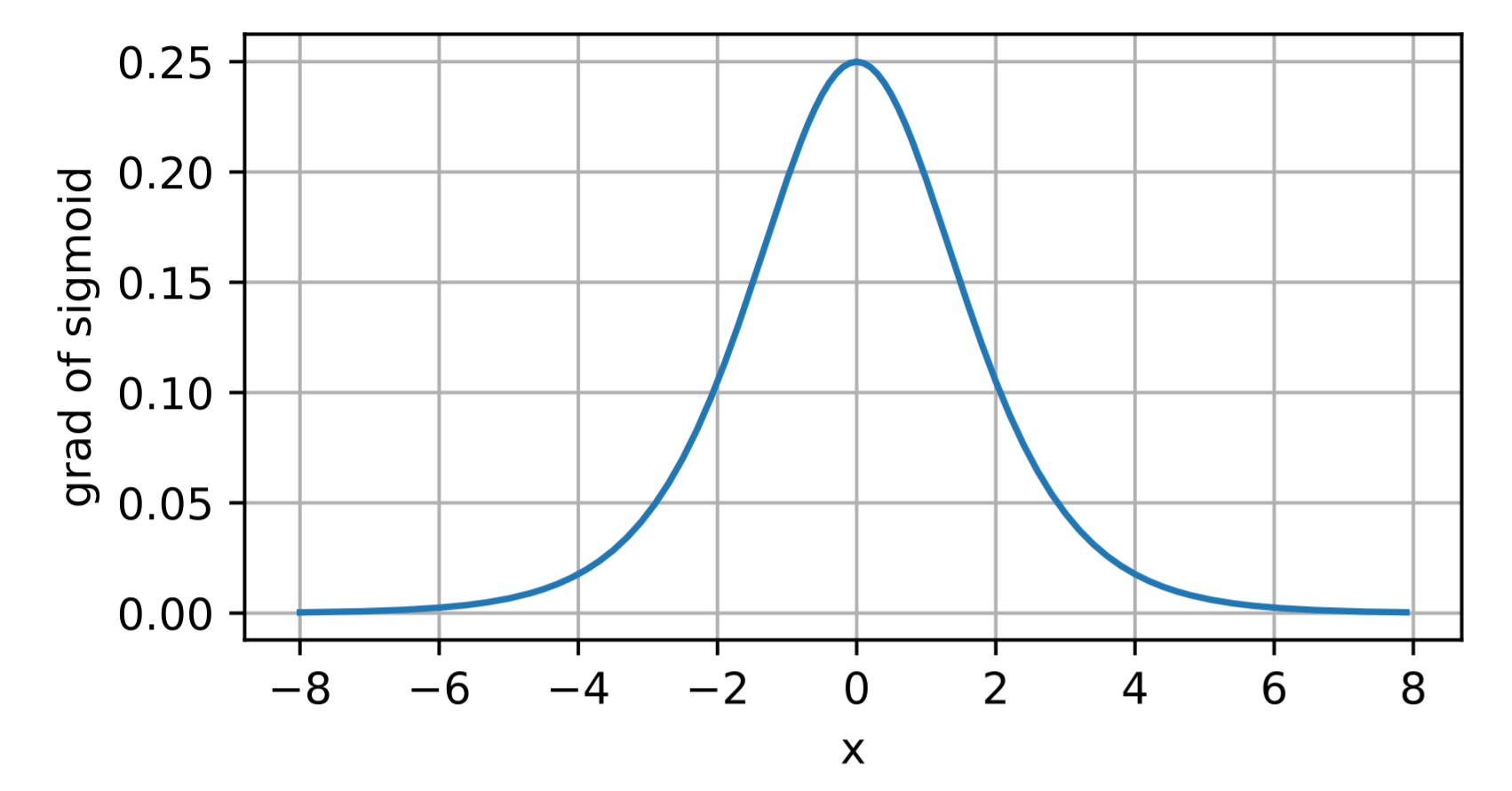 **注意**:当输入为0时,sigmoid函数的导数达到最大值0.25; 而输入在任一方向上越远离0点时,导数越接近0。
**注意**:当输入为0时,sigmoid函数的导数达到最大值0.25; 而输入在任一方向上越远离0点时,导数越接近0。
- Tanh函数
与sigmoid函数类似,tanh(双曲正切)函数也能将其输入压缩转换到区间 上。 tanh 函数的公式如下:
tanh函数的导数是:
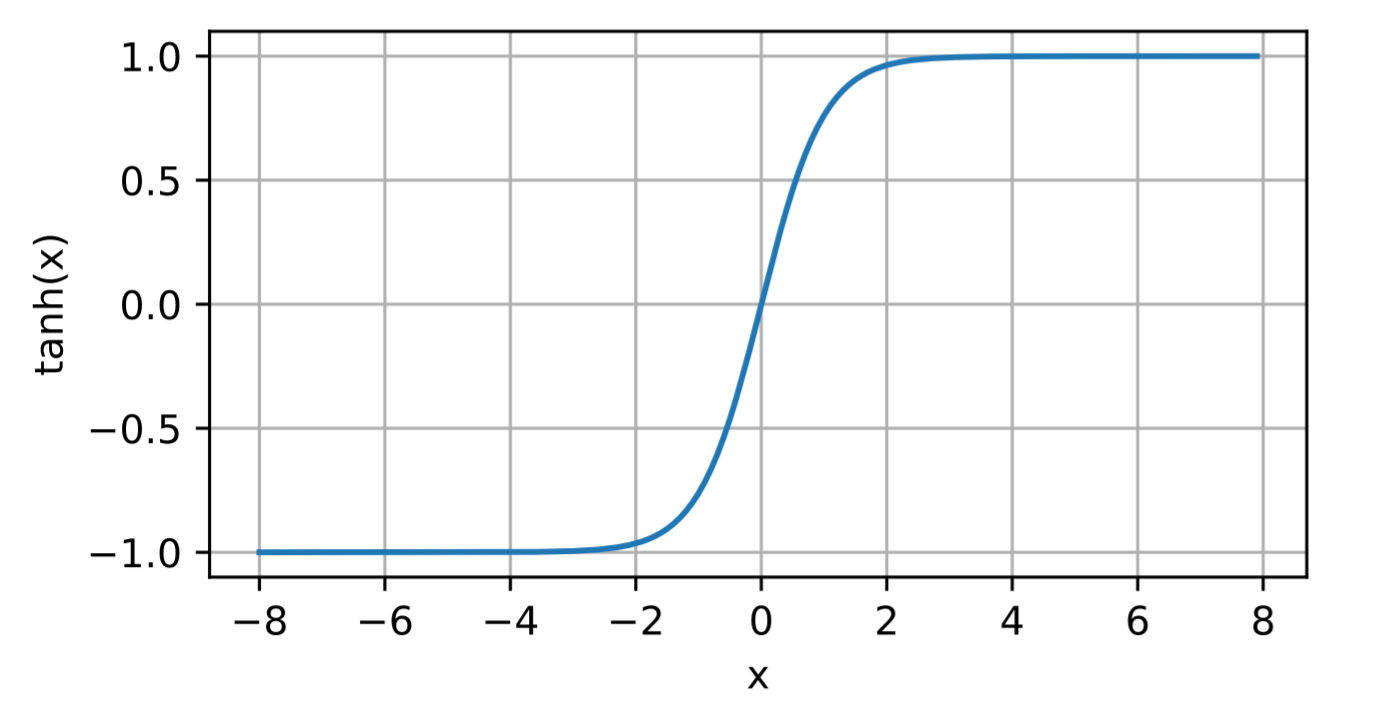
为了直观感受一下,可以画出函数的曲线图。 正如从图中所看到,当输入在0附近时,tanh函数接近线性变换。 函数的形状类似于sigmoid函数, 不同的是tanh函数关于坐标系原点中心对称。
1 | y = torch.tanh(x) |
Results:
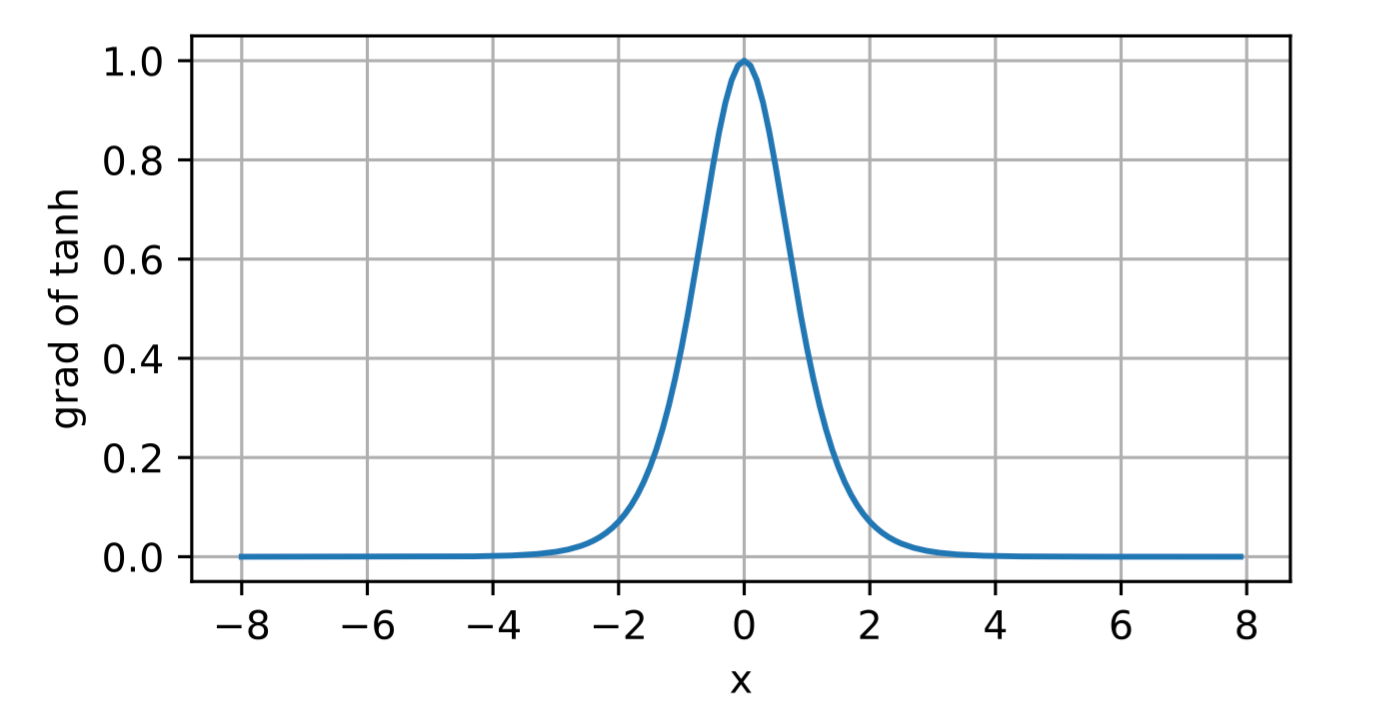
 - Tanh 函数的导数
- Tanh 函数的导数
1 | # 清除以前的梯度 |
Results:
- ReLU 函数
最受欢迎的激活函数是修正线性单元(Rectified linear unit,ReLU),因为它实现简单,同时在各种预测任务中表现良好。 ReLU 提供了一种非常简单的非线性变换。
使用 ReLU 的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。这使得优化表现的更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题
给定元素 , ReLU 函数被定义为该元素与 0 的最大值:
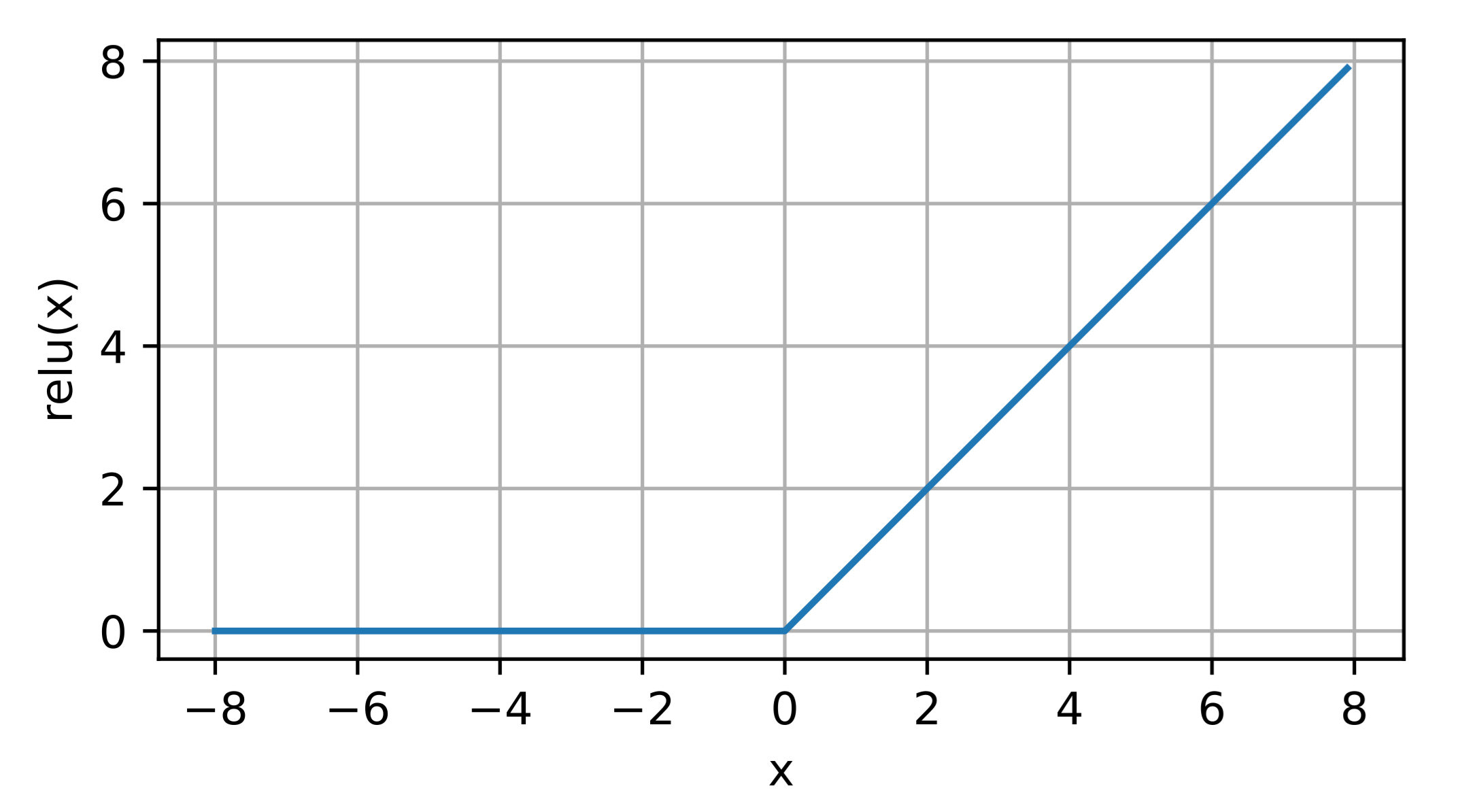
为了直观感受一下,可以画出函数的曲线图。 正如从图中所看到,激活函数是分段线性的。
1 | %matplotlib inline |
Results:
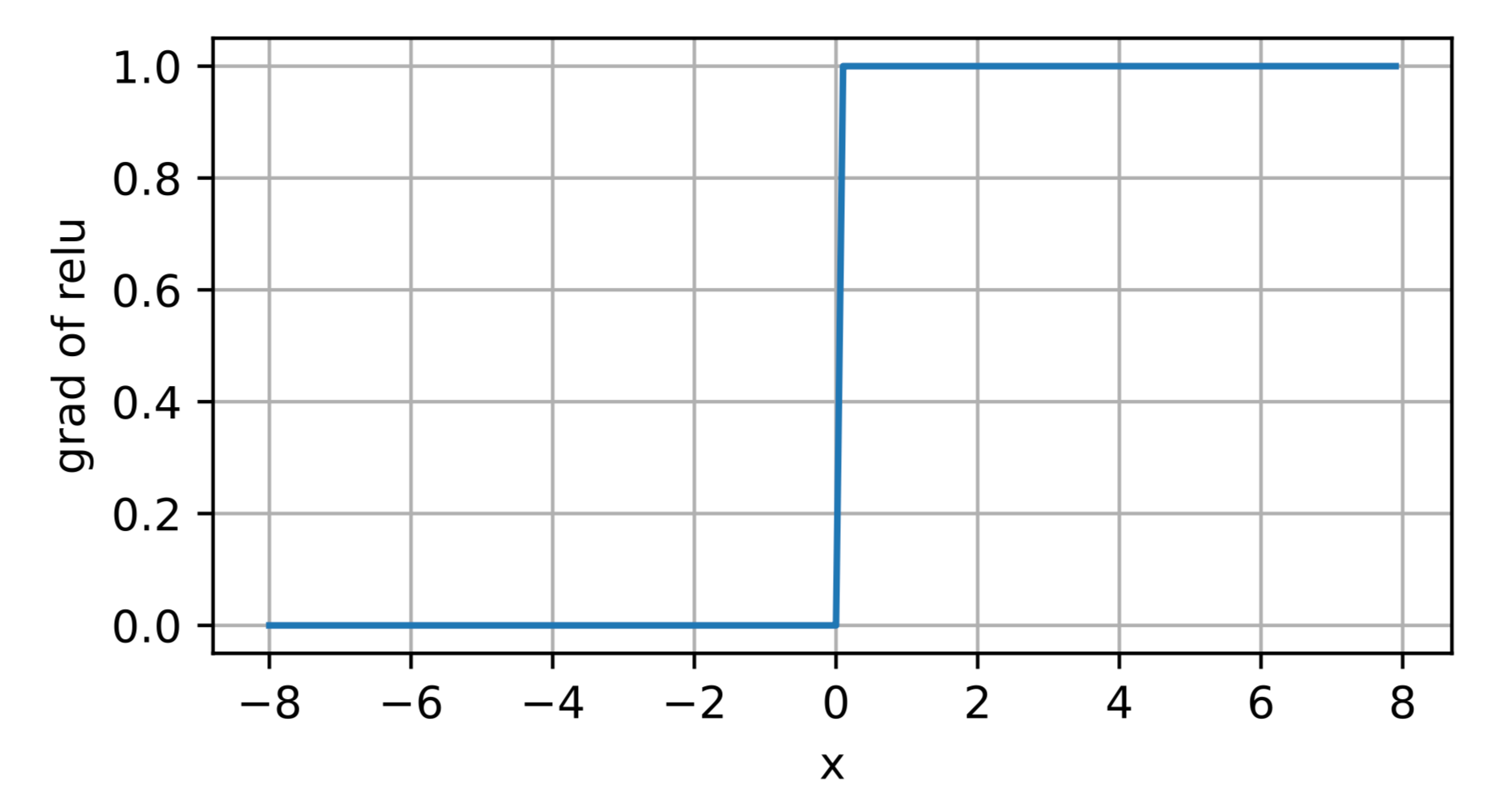
Note:当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。 注意,当输入值精确等于0时,ReLU函数不可导。
- ReLU函数的导数
1 | y.backward(torch.ones_like(x), retain_graph=True) |
Results:
3.1.2.4 多类分类
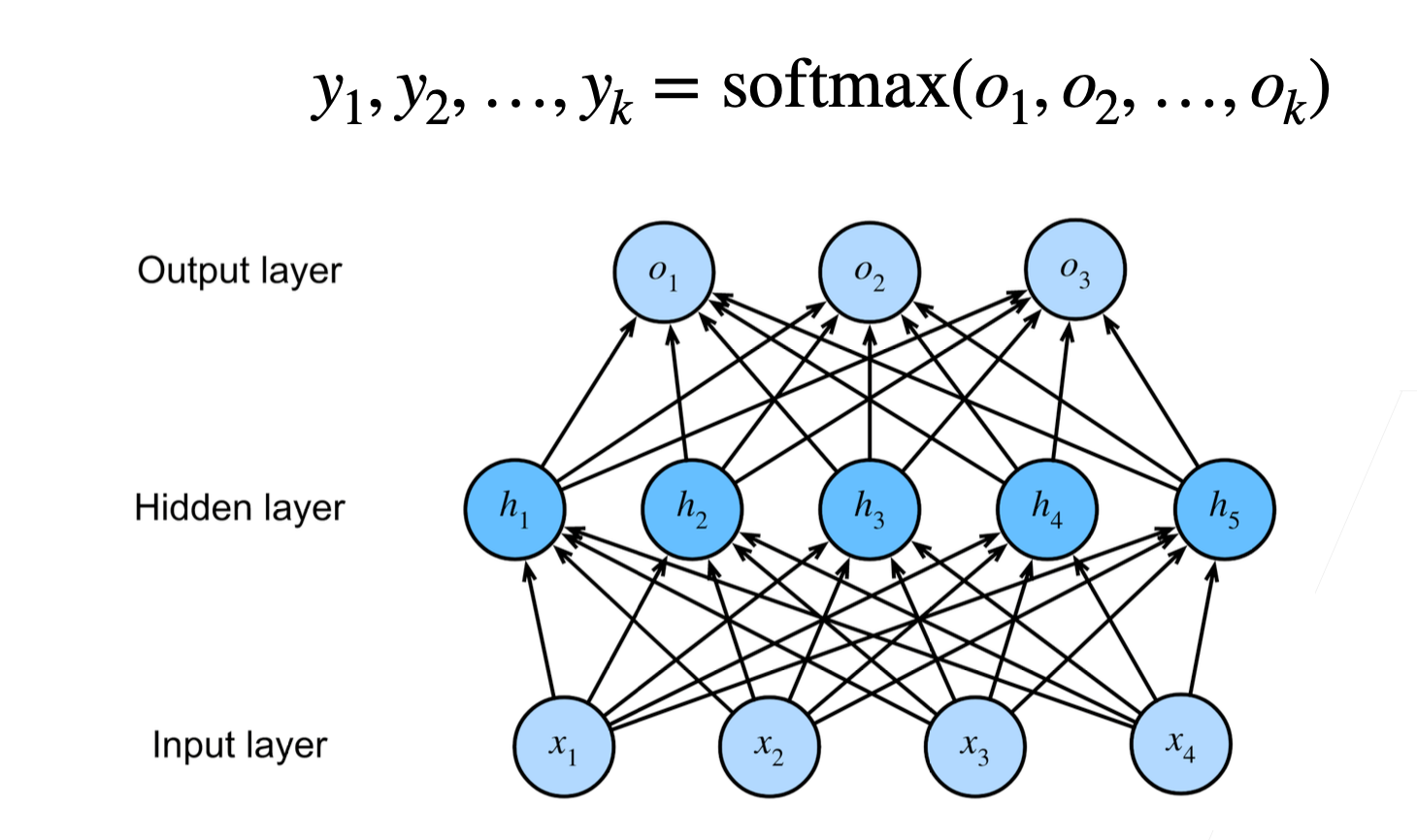 - **输入**:$\mathbf{x} \in \mathbb{R}^n$
- **隐藏层**:
$$
\mathbf{h}=\sigma\left(\mathbf{W}_1 \mathbf{x}+\mathbf{b}_1\right)
$$
其中,$\mathbf{W}_1 \in \mathbb{R}^{m \times n}, \mathbf{b}_1 \in \mathbb{R}^m$,$\sigma$ 是按元素的激活函数。
- **输出层**:
$$
\begin{aligned}
o &=\mathbf{w}_2^T \mathbf{h}+b_2 \\
y &= \textrm{softmax}(\mathbf{o})
\end{aligned}
$$
其中,$\mathbf{w}_2 \in \mathbb{R}^{m\times k}, b_2 \in \mathbb{R}^k$
- **输入**:$\mathbf{x} \in \mathbb{R}^n$
- **隐藏层**:
$$
\mathbf{h}=\sigma\left(\mathbf{W}_1 \mathbf{x}+\mathbf{b}_1\right)
$$
其中,$\mathbf{W}_1 \in \mathbb{R}^{m \times n}, \mathbf{b}_1 \in \mathbb{R}^m$,$\sigma$ 是按元素的激活函数。
- **输出层**:
$$
\begin{aligned}
o &=\mathbf{w}_2^T \mathbf{h}+b_2 \\
y &= \textrm{softmax}(\mathbf{o})
\end{aligned}
$$
其中,$\mathbf{w}_2 \in \mathbb{R}^{m\times k}, b_2 \in \mathbb{R}^k$
3.1.2.5 多隐藏层
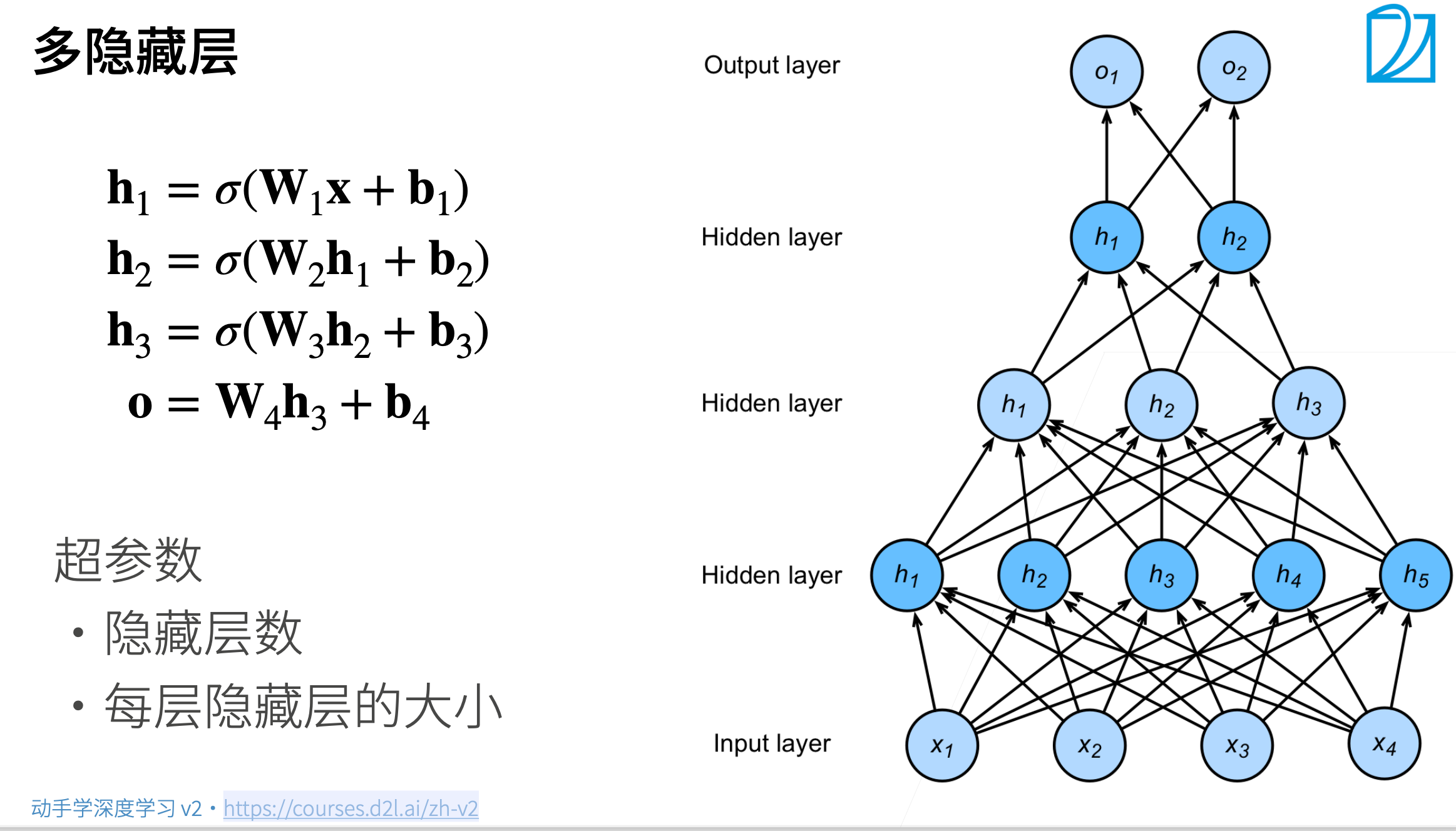 $$
\begin{aligned}
\mathbf{h}_1 & =\sigma\left(\mathbf{W}_1 \mathbf{x}+\mathbf{b}_1\right) \\
\mathbf{h}_2 & =\sigma\left(\mathbf{W}_2 \mathbf{h}_1+\mathbf{b}_2\right) \\
\mathbf{h}_3 & =\sigma\left(\mathbf{W}_3 \mathbf{h}_2+\mathbf{b}_3\right) \\
\mathbf{o} & =\mathbf{W}_4 \mathbf{h}_3+\mathbf{b}_4
\end{aligned}
$$
$$
\begin{aligned}
\mathbf{h}_1 & =\sigma\left(\mathbf{W}_1 \mathbf{x}+\mathbf{b}_1\right) \\
\mathbf{h}_2 & =\sigma\left(\mathbf{W}_2 \mathbf{h}_1+\mathbf{b}_2\right) \\
\mathbf{h}_3 & =\sigma\left(\mathbf{W}_3 \mathbf{h}_2+\mathbf{b}_3\right) \\
\mathbf{o} & =\mathbf{W}_4 \mathbf{h}_3+\mathbf{b}_4
\end{aligned}
$$
超参数:
- 隐藏层数
- 每层隐藏层大小
3.1.2.6 练习
- 证明一个仅使用ReLU(或pReLU)的多层感知机构造了一个连续的分段线性函数。00:08
绘制出RELU的图像后,我们可以发现,输出值在经过下一层隐藏层的计算后,如果结果小于等于0,则这个数据被舍弃,结果大于0则被保留,类似一个筛选的过程。相当于上一层的输出经过线性变换后在下一层被筛选,线性变换和上述筛选的过程都是连续的,因此就会产生连续而且分段的结果。
- 构建多个超参数的搜索方法。
有四种主要的策略可用于搜索最佳配置。
- 试错
- 网格搜索
- 随机搜索
- 贝叶斯优化
- 权重初始化方法
- 全零初始化:在神经网络中,把w初始化为0是不可以的。这是因为如果把w初始化0,那么每一层的神经元学到的东西都是一样的(输出是一样的),而且在BP的时候,每一层内的神经元也是相同的,因为他们的gradient相同,weight update也相同。
- 随机初始化
- Xavier初始化:保持输入和输出的方差一致(服从相同的分布),这样就避免了所有输出值都趋向于0。
- He initialization:在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0(x负半轴中是不激活的),所以要保持variance不变,只需要在Xavier的基础上再除以2。
- pre-training
详见权重/参数初始化
- 超参数的调节
- 在mlp中,第一个隐藏的的单元数可能大于输入的个数,每个隐藏层中的单元数由前至后递减,逐渐接近输出的个数。
- 多数情况下,将mlp的深度设置得较深,而每层的单元数相对较少,这样易于训练,不易过拟合,也利于逐步学习样本特征。
- 激活函数种类的选择对训练的影响小于其余的因素。
3.1.2.7 总结
- 多层感知机使用隐藏层和激活函数来得到非线性模型
- 常用激活函数:Sigmoid,Tanh,ReLU
- 使用softmax进行多分类
- 隐藏层数、大小为超参数
3.1.3 从零实现多层感知机
在 [[dl-notes-2#2.2.5.5 训练|Softmax 简洁实现]] 中,笔者在尝试运行李沐老师的代码时会报错,此处,对其进行修正。
通过查询发现,笔者安装的 d2l 是最新版本:
1 | d2l==1.0.0a0 |
发现这个版本中并没有 d2l.train_ch3 函数,因此,考虑将版本进行倒退:
1 | pip install d2l==0.17.5 |
然而,此时 import d2l 包时会报 [[dl-notes-2#2.1.3.1 环境配置|环境配置]] 中出现的错误:
1 | !pip install d2l |
会报如下错误:
1 | ValueError Traceback (most recent call last) |
此时只需要重装 pandas 就可以完美解决了。
1 | !pip install --upgrade numpy |
3.1.3.1 读取数据
我们已经在 [[dl-notes-2#3.1.2 多层感知机|上一节]] 中描述了多层感知机(MLP),接下来让我们尝试自己实现一个多层感知机。
为了与之前 [[dl-notes-2#2.2.4 从零实现 Softmax回归|softmax回归]] 获得的结果进行比较,我们将继续使用 Fashion-MNIST [[dl-notes-2#2.2.3 图片分类数据集|图像分类数据集]]。
1 | import torch |
3.1.3.2 初始化模型参数
Fashion-MNIST 中的每个图像由 个灰度像素值组成。所有图像共分为 10 个类别。忽略像素之间的空间结构,我们可以将每个图像视为具有 784 个输入特征和 10 个类的简单分类数据集。
首先,我们将实现一个具有单隐藏层的多层感知机,它包含 256 个隐藏单元。通常,我们选择 2 的若干次幂作为层的宽度。因为内存在硬件中的分配和寻址方式,这么做往往可以在计算上更高效。
我们用几个张量来表示我们的参数。注意,对于每一层我们都要记录一个权重矩阵和一个偏置向量。跟以前一样,我们要为损失关于这些参数的梯度分配内存。
1 | num_inputs, num_outputs, num_hiddens = 784, 10, 256 |
3.1.3.3 模型设定
实现relu激活函数:
1 | def relu(X): |
构建模型:
因为我们忽略了空间结构,所以我们使用 reshape 将每个二维图像转换为一个长度为 num_inputs 的向量。只需几行代码就可以实现我们的模型。
1 | def net(X): |
损失函数:
1 | loss = nn.CrossEntropyLoss(reduction='none') |
训练:
多层感知机的训练过程与 softmax 回归的训练过程完全相同。可以直接调用 d2l 包的 train_ch3 函数(如果运行报错,提示 d2l.train_ch3 不存在,请查看 [[dl-notes-2#3.1.3 从零实现多层感知机|本章前沿部分]] 的解决方案)。
将迭代周期数设置为 10 ,并将学习率设置为 0.1 :
1 | num_epochs, lr = 10, 0.1 |
Results:
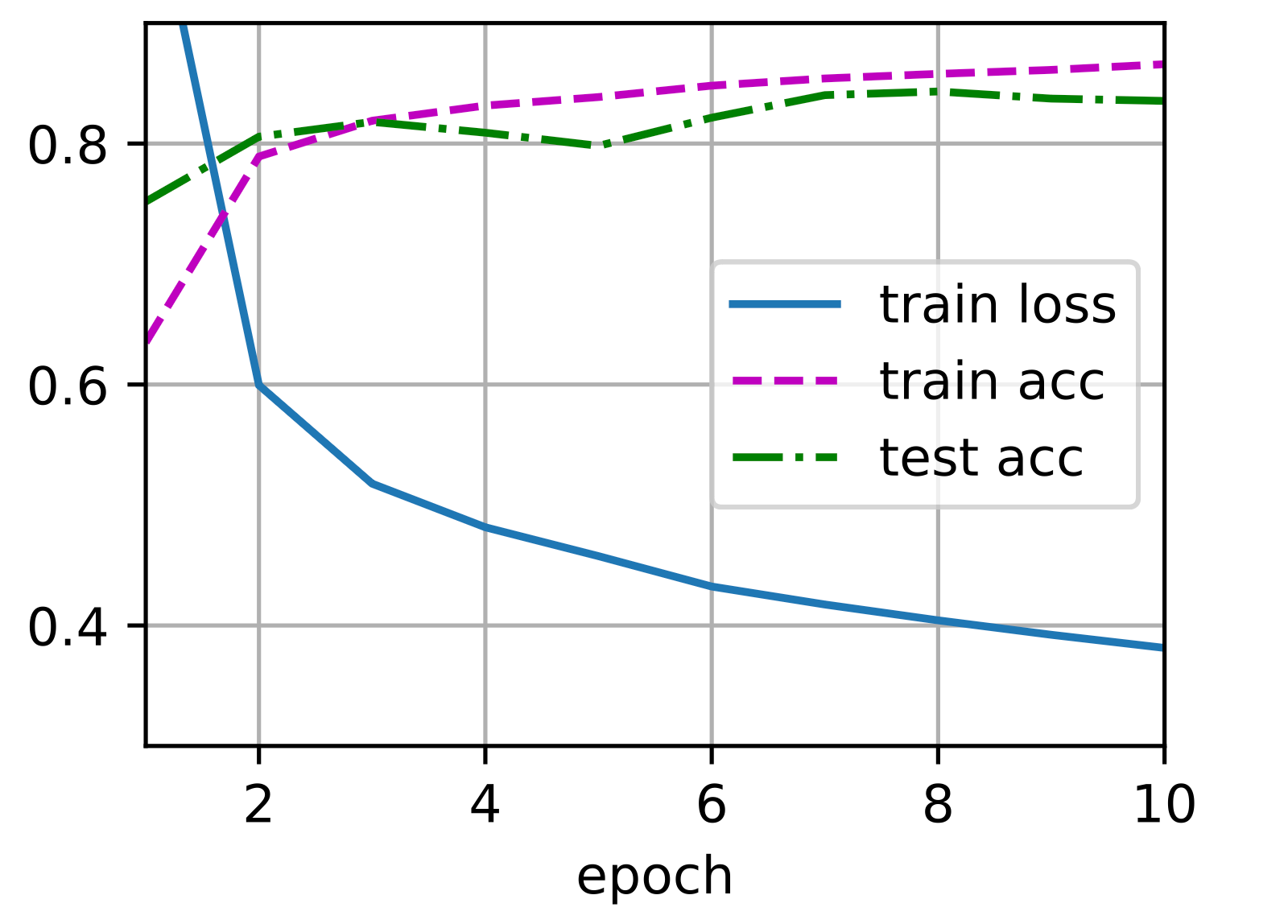
为了对学习到的模型进行评估,我们将在一些测试数据上应用这个模型。
1 | d2l.predict_ch3(net, test_iter) |
Results:
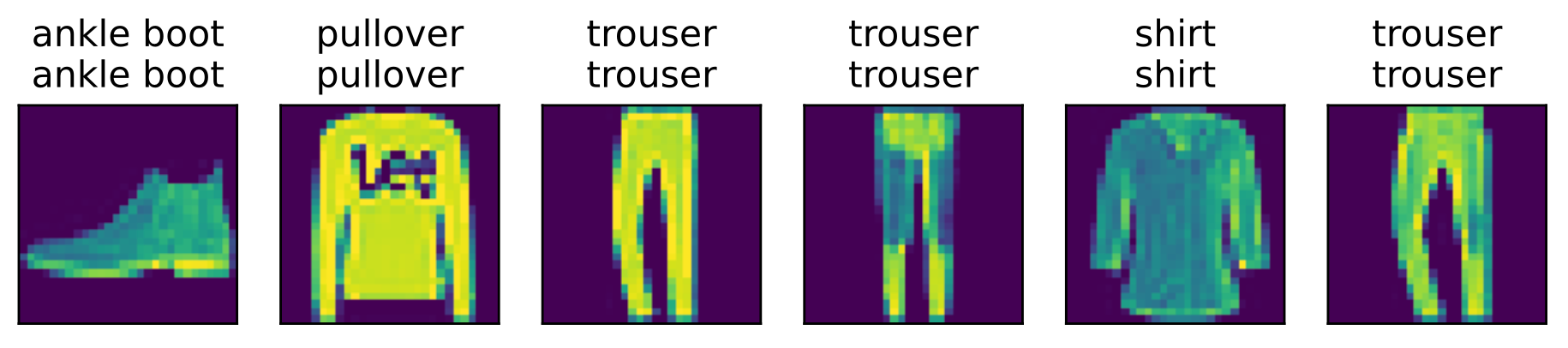
3.1.3.4 小结
手动实现一个简单的多层感知机是很容易的。然而如果有大量的层,从零开始实现多层感知机会变得很麻烦(例如,要命名和记录模型的参数)。
3.1.4 多层感知机Q&A
3.2 模型选择和过拟合
3.2.1 模型选择
案例:预测谁会偿还贷款:
-
Q:给定100个贷款申请人的信息,其中五个人在3年内违约了,模型通过训练发现了强信号:所有的五个人在面试时都穿了蓝色衬衫。
-
A:这当然是不对的。
3.2.1.1 训练集和测试集相关概念
-
训练误差和泛化误差
- 训练误差:模型在训练数据上的误差
- 泛化误差:模型在新数据上的误差。 泛化误差是我们所最关心的
-
验证数据集和测试数据集
- 验证数据集:一个用来评估模型好坏的数据集(如拿出50%的训练数据)
- Note:不要跟训练数据混在一起(常犯错误)
- 测试数据集:只用一次的数据集。(如:未来的考试)
二者最大的区别:验证数据集可以那来用很多次,相当于平时的模拟考,而测试数据集则只能用一次来评估模型的性能,相当于最终的考试。
- 验证数据集:一个用来评估模型好坏的数据集(如拿出50%的训练数据)
-
K-则交叉验证
- 在没有足够多数据时使用(这是常态)
目的:在没有足够多数据使用时评估模型和超参数的性能,也就是说,K次训练和验证使用的是相同的超参数和模型
3.2.1.2 总结
- 训练数据集:训练模型参数
- 验证数据集:选择模型超参数
- 非大数据集上通常使用k-则交叉验证
3.2.2 过拟合和欠拟合
3.2.2.1 模型复杂度
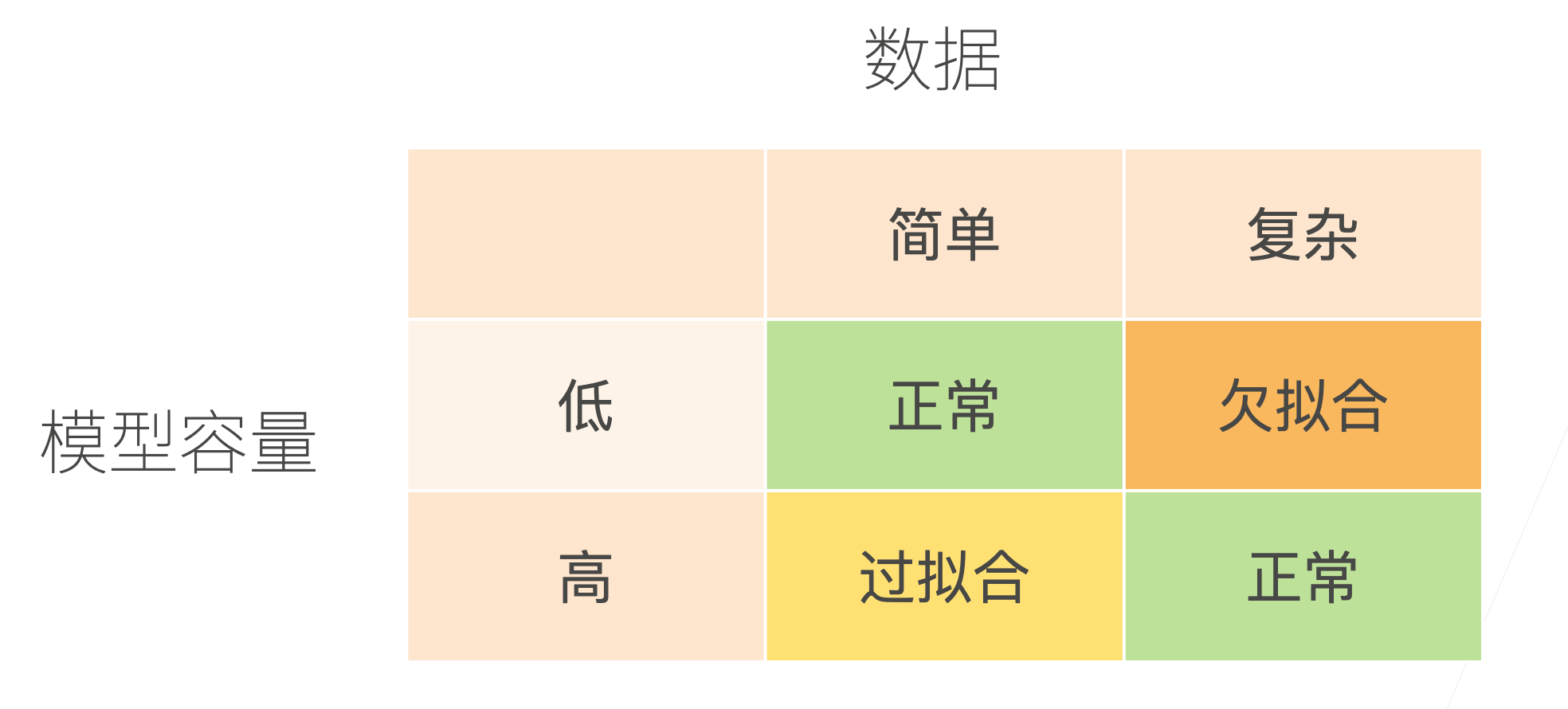 **模型容量**:即模型的复杂度,也代表了模型拟合各种函数的能力。
- 低容量的模型难以拟合训练数据
- 高容量的模型可以记住所有的训练数据
**模型容量**:即模型的复杂度,也代表了模型拟合各种函数的能力。
- 低容量的模型难以拟合训练数据
- 高容量的模型可以记住所有的训练数据
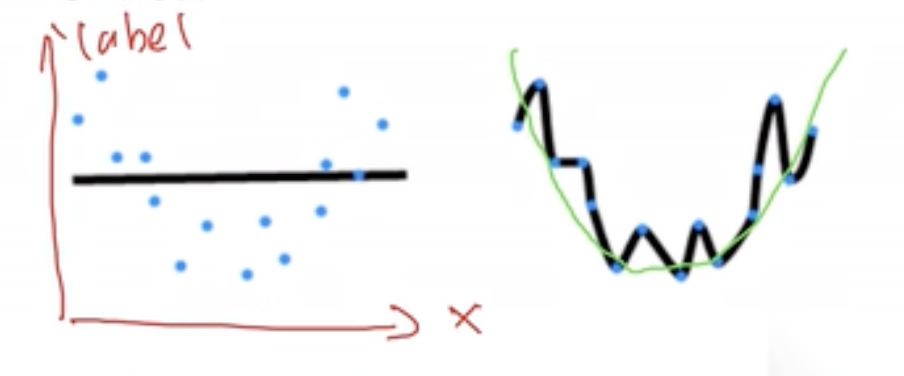 显然,模型容量太低或太高都不好:
- 太低(对应第一种)过于简单,模型分类效果差,
- 太高(对应第二种)则过于复杂,把噪声全部都拟合住了。
显然,模型容量太低或太高都不好:
- 太低(对应第一种)过于简单,模型分类效果差,
- 太高(对应第二种)则过于复杂,把噪声全部都拟合住了。
模型容量的影响:
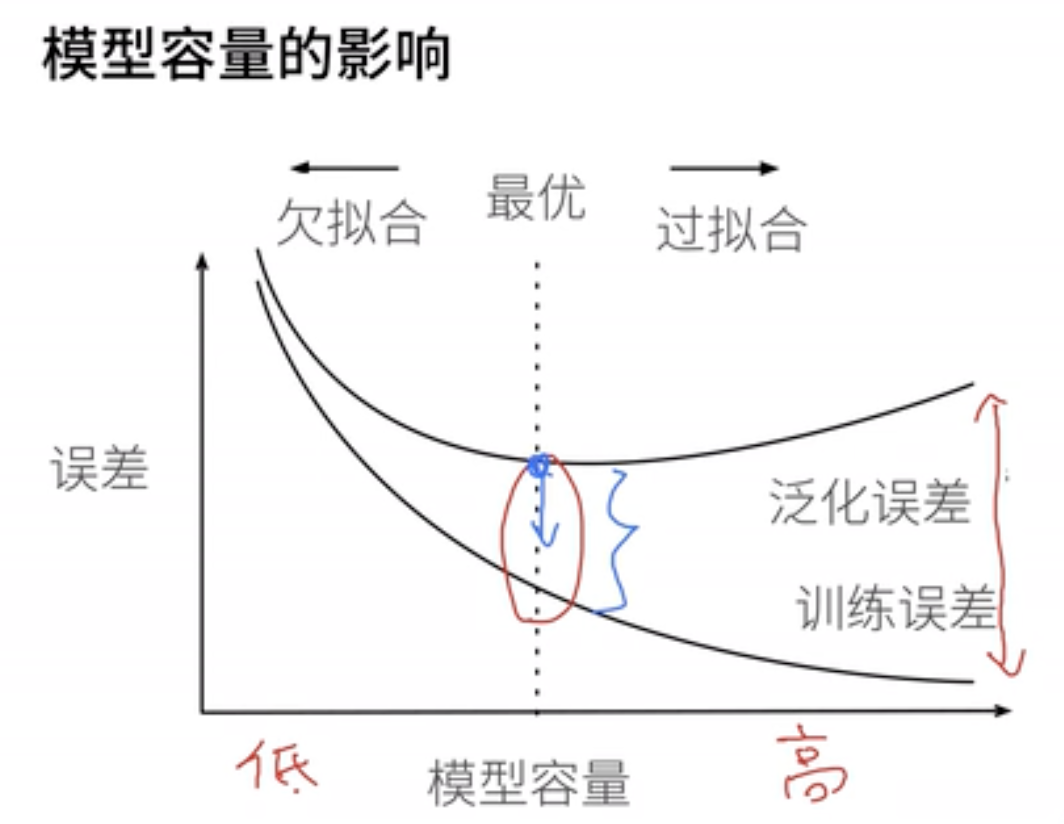
- 深度学习的核心任务就是把泛化误差往下降。
- 有时为了降低泛化误差,不得不承受一定程度的过拟合。
- 首先模型大,然后再使用各种手段控制模型容量使得泛化误差下降。
估计模型容量:
- 难以在不同的种类算法之间比较
- 例如树模型和神经网络
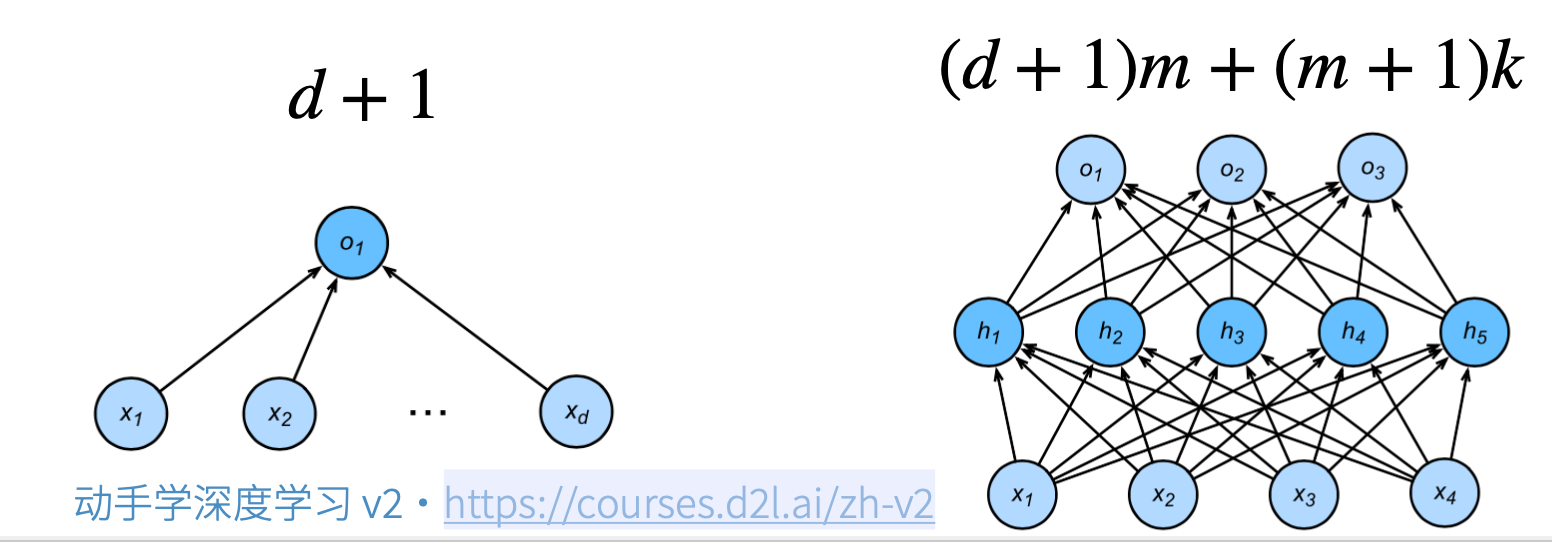
- 给定一个模型种类,将有两个主要因素
- 参数的个数
- 参数的选择范围
 #### 3.2.2.2 VC维
#### 3.2.2.2 VC维
VC维:统计学习理论的一个核心思想,这里大致了解就行,因为很难计算之后学习的模型(如CNN,RNN)的 VC 维,故并不经常用:
-
定义:对于一个分类模型,
VC维等于一个最大的数据集的大小,不管如何给定标号,都存在一个模型对它进行完美分类。即存在 个样本,模型能把 个样本的 种标号方式打散的 的最大值。 -
例子:线性分类器的
VC维-
2 维输入的感知机,VC 维 = 3
对于三个点的任意标号都能分类,而任意四个点的样本都存在不能被打散的标号形式个,如之前讲过的
XOR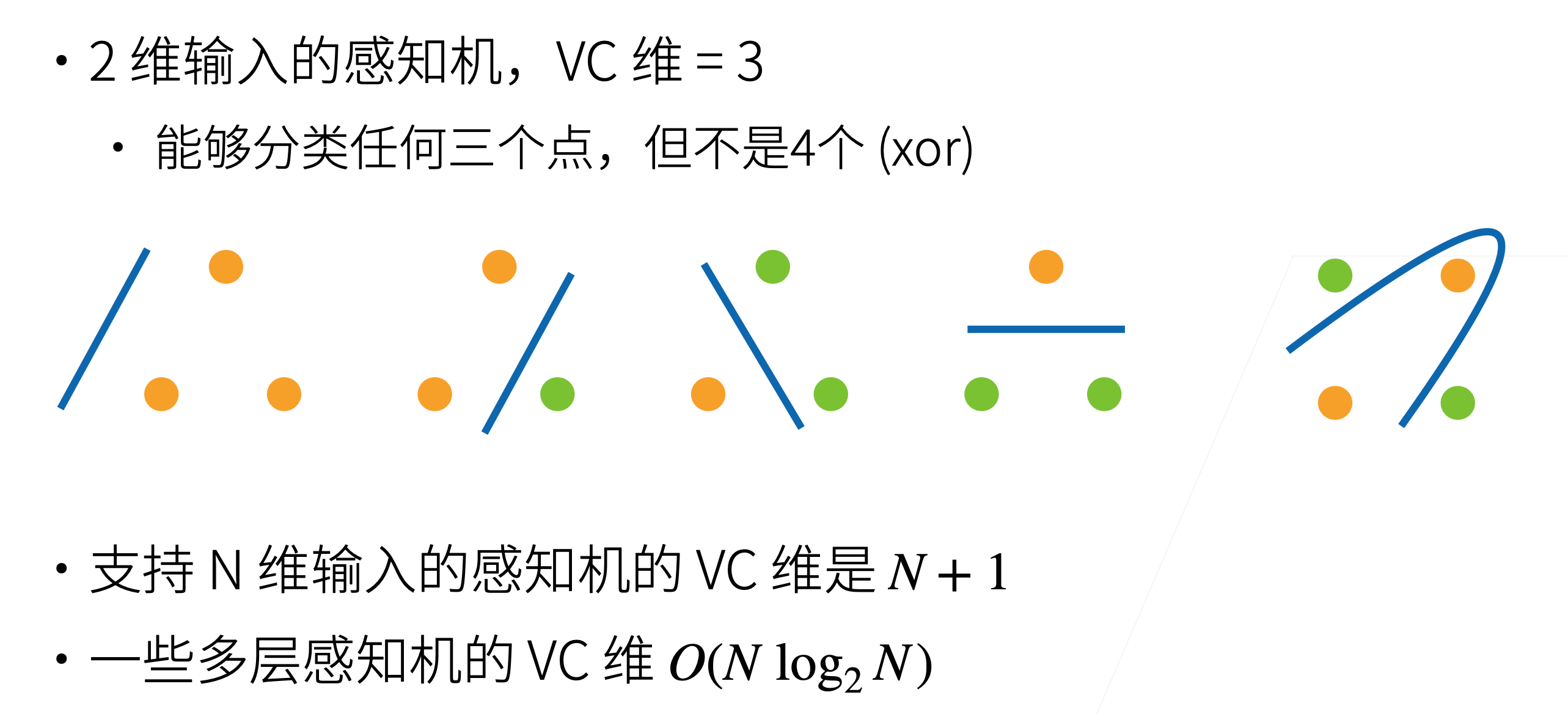
-
-
支持N维输入的感知机的
VC维是 -
一些多层感知机的
VC维是
VC维的用处
- 提供为什么一个模型好的理论依据
- 它可以衡量训练误差和泛化误差之间的间隔
- 但深度学习中很少使用
- 衡量不是很准确
- 计算深度学习模型的
VC维很困难
3.2.2.3 数据复杂度
- 多个重要因素
- 样本的元素个数
- 每个样本的元素个数
- 时间、空间结构
- 多样性
3.2.3 总结
- 模型容量需要匹配数据复杂度,否则可能导致欠拟合和过拟合
- 统计机器学习提供数学工具来衡量模型复杂度
- 实际中一般考观察训练误差和验证误差
3.3 多项式回归
- 本小节使用多项式回归为例子,在
pytorch上展示过拟合和欠拟合的实际表现
3.3.1 导入库
1 | import math |
3.3.2 生成数据集
给定 ,我们将使用以下三阶多项式来生成训练和测试数据的标签:
噪声项 服从均值为 且标准差为 的正态分布。
- 在优化的过程中,通常希望避免非常大的梯度值或损失值。
- 因此此处,将特征从 调整为 ,这样可以避免很大的 带来的特别大的指数值。
1 | max_degree = 20 # 多项式的最大阶数 |
- Note:存储在
poly_features中的单项式由gamma函数重新缩放,其中 。
3.3.3 NumPyndarray 转换为tensor
1 | true_w, features, poly_features, labels = [torch.tensor(x, dtype= |
Results:
1 | (tensor([[0.2658], |
3.3.4 模型训练和测试
- 评估损失函数
1 | def evaluate_loss(net, data_iter, loss): #@save |
- 训练函数
1 | def train(train_features, test_features, train_labels, test_labels, |
3.3.5 拟合
3.3.5.1 三阶多项式函数拟合(正态)
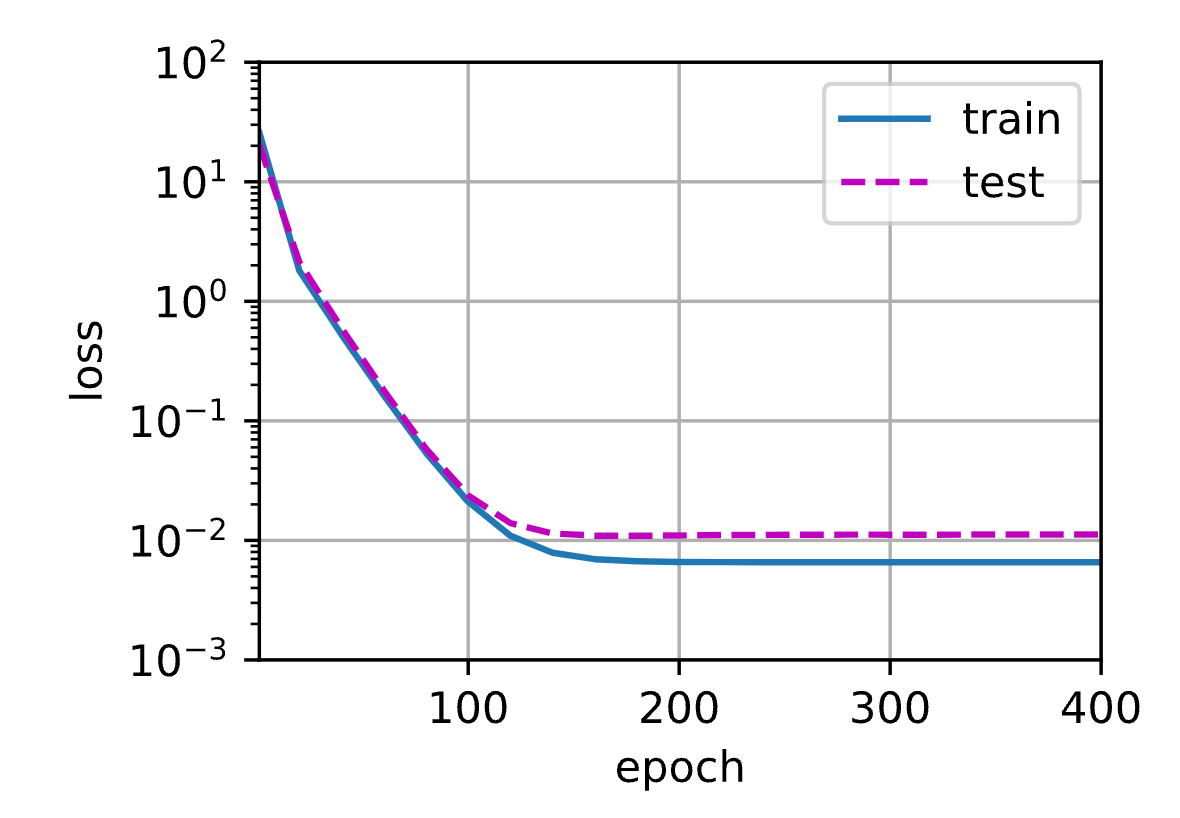
我们将首先使用三阶多项式函数,它与数据生成函数的阶数相同。 结果表明,该模型能有效降低训练损失和测试损失。 学习到的模型参数也接近真实值 。
1 | # 从多项式特征中选择前4个维度,即1,x,x^2/2!,x^3/3! |
Results:
1 | weight: [[ 4.9753904 1.1974537 -3.3913007 5.6012864]] |
3.3.5.2 线性函数拟合(欠拟合)
1 | # 从多项式特征中选择前2个维度,即1和x |
Results:
1 | weight: [[3.366678 4.3843927]] |
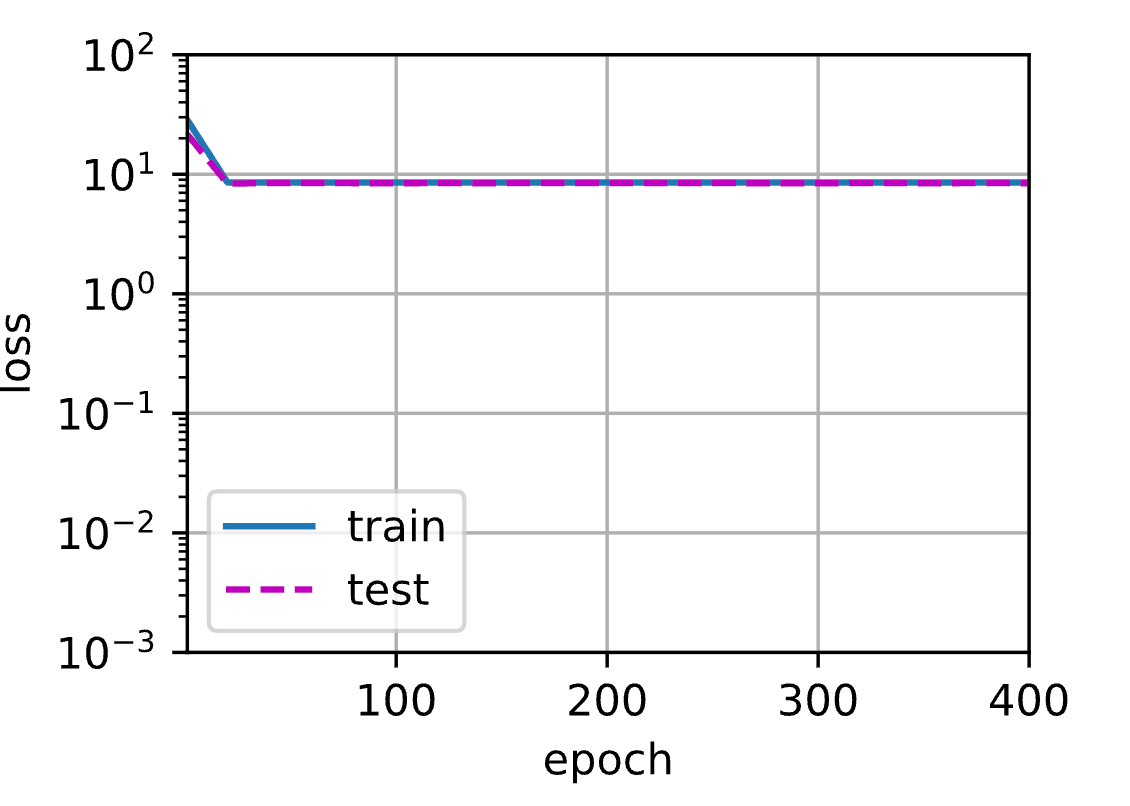 可以发现,在最后一个迭代周期完成后,训练损失仍然很高。 当用来拟合非线性模式(如这里的三阶多项式函数)时,线性模型容易欠拟合。
可以发现,在最后一个迭代周期完成后,训练损失仍然很高。 当用来拟合非线性模式(如这里的三阶多项式函数)时,线性模型容易欠拟合。
3.3.5.3 高阶多项式函数拟合(过拟合)
1 | # 从多项式特征中选取所有维度 |
Results:
1 | weight: [[ 4.9389434 1.2975892 -3.20294 5.0837035 -0.6047161 1.3912908 |
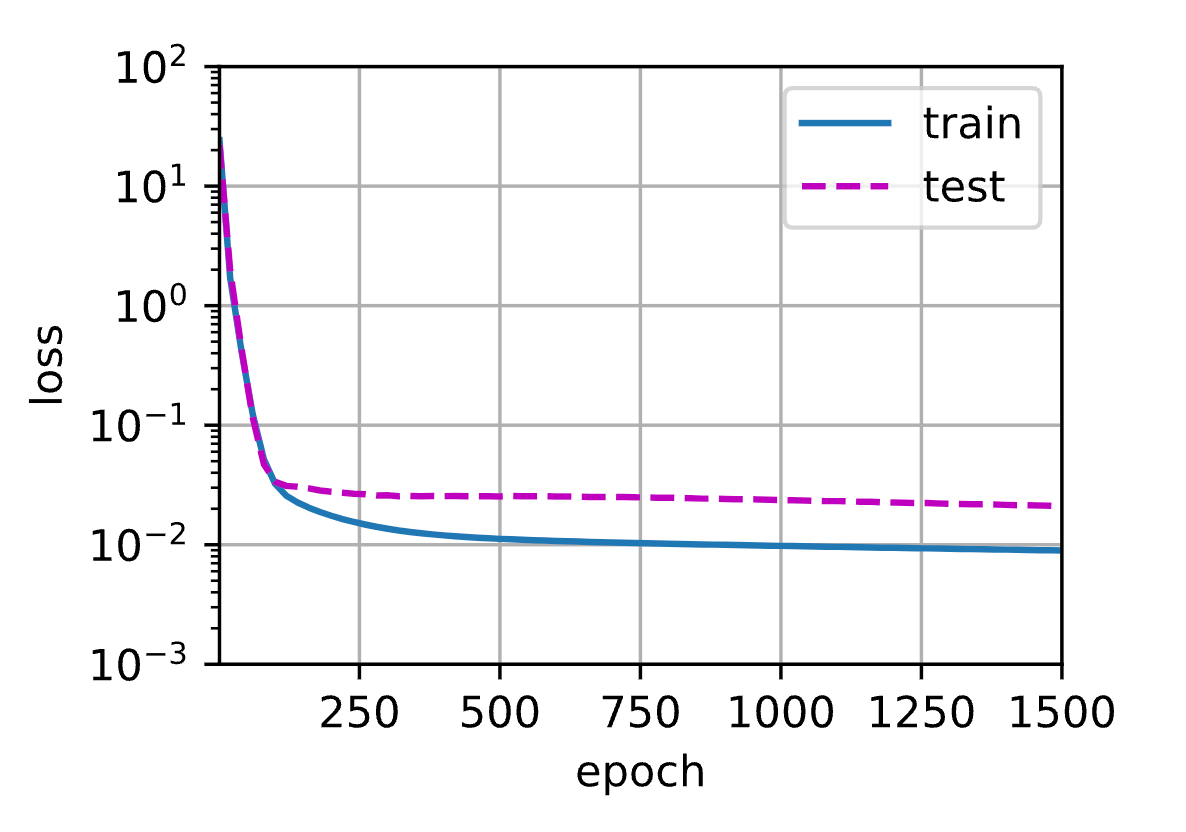 ### 3.3.5 小结
### 3.3.5 小结
- 欠拟合 是指模型无法继续减少训练误差。过拟合 是指训练误差远小于验证误差。
- 由于不能基于训练误差来估计泛化误差,因此简单地最小化训练误差并不一定意味着泛化误差的减小。
- 机器学习模型需要注意防止过拟合,即防止泛化误差过大。
- 验证集可以用于模型选择,但不能过于随意地使用它。
- 应该选择一个复杂度适当的模型,避免使用数量不足的训练样本
3.4 权重衰退
3.4.1 权重限制
 权重衰退是最常见的一种处理过拟合的方法,是最广泛使用的正则化技术之一。
权重衰退是最常见的一种处理过拟合的方法,是最广泛使用的正则化技术之一。
其中权重衰退属于第二种方法。
3.4.1.1 硬性限制/直观理解
优化目标:仍然是 ,只是额外对 添加一个限制条件 ,即权重的各项平方和小于一个特定的常数 。那么设定一个较小的 就会使得 中每个元素的值都不会太大。
通常不会限制偏移 ,理论上讲 表示整个数据在零点上的偏移,因此是不应该限制的,但实践中限制与否对结果都没什么影响。
吴恩达课程中对这一现象的解释是 是高维向量,已经包含了绝大多数参数足以表达高方差问题,b作为单个数字对结果的影响就会很小.
小的 意味着更强的正则项,对于相同的 , 中元素越多则单个元素的值会越小。
3.4.1.2 柔性限制/实际应用
可以通过拉格朗日乘子证明对于每个 都可以找到 使得硬性限制的目标函数等价于上式。
其中 这一项被称为罚 (penalty), 是超参数,控制了正则项的重要程度。
当 时无作用, 时最优解 ,也就是说 越大模型复杂度就被控制的越低。
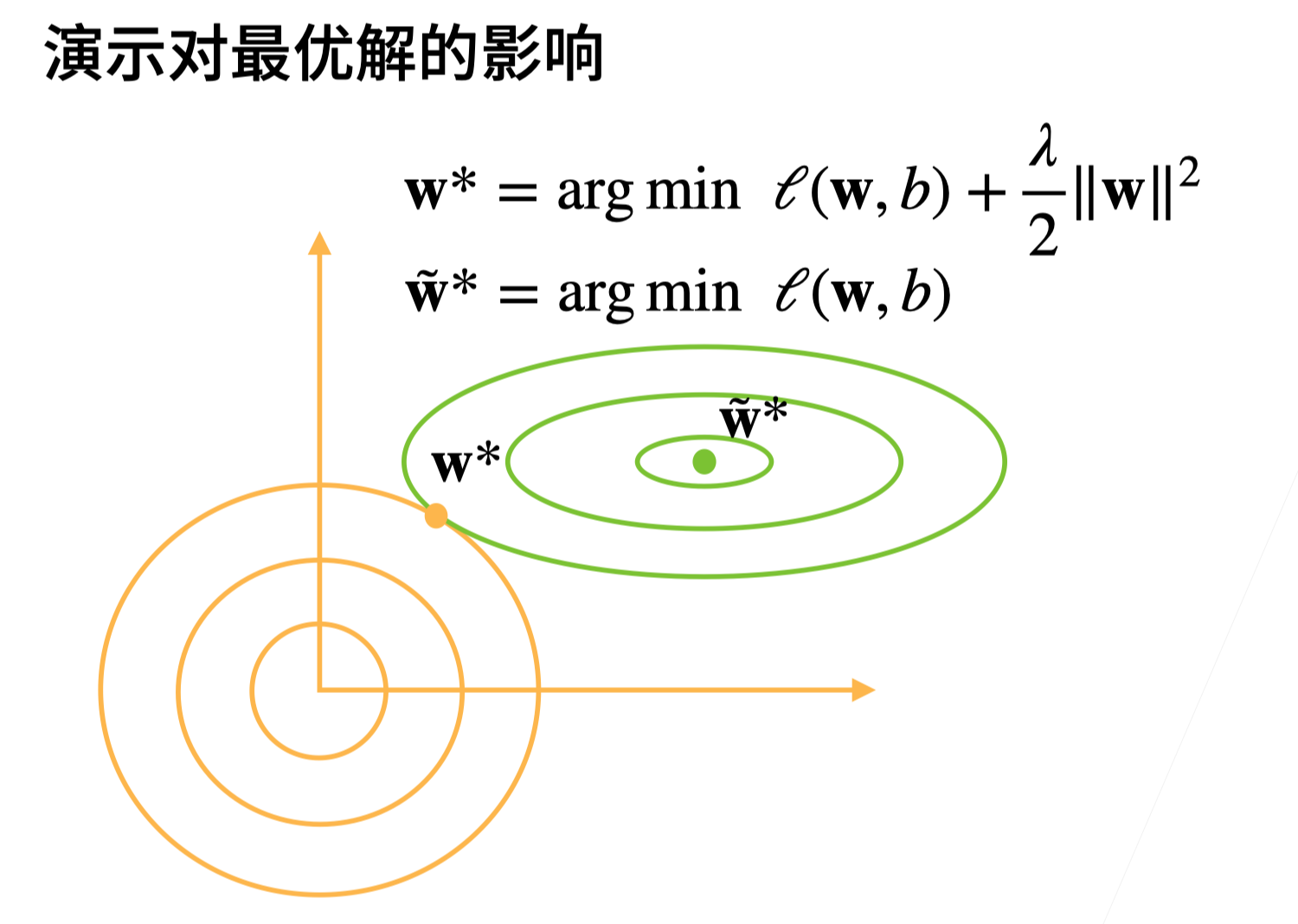
为什么我们首先使用范数,而不是范数?
事实上,这个选择在整个统计领域中都是有效的和受欢迎的。 正则化线性模型构成经典的 岭回归(ridge regression)算法, 正则化线性回归是统计学中类似的基本模型,通常被称为 套索回归(lasso regression)。
使用范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。在实践中,这可能使它们对单个变量中的观测误差更为稳定。
相比之下,惩罚会导致模型将权重集中在一小部分特征上,而将其他权重清除为零。这称为特征选择(feature selection),这可能是其他场景下需要的。
3.4.2 参数更新
- 计算梯度
- 时间 更新参数
注意到这个公式中后一项与原来更新参数的公式没有区别,仅仅是在前一项 上加了一个系数 。通常 ,也就是说由于引入了 ,每次更新参数前先给待更新参数乘上一个小于 的权重再更新,权重衰退由此得名。
3.4.3 代码实现
3.4.3.1 从零实现
下面我们将从头开始实现权重衰减,只需将的平方惩罚添加到原始目标函数中。
- 初始化模型参数
定义一个函数来随机初始化模型参数。
1 | def init_params(): |
- 定义 范数惩罚
对所有项求平方后求和。
1 | def l2_penalty(w): |
- 定义训练代码实现
下面的代码将模型拟合训练数据集,并在测试数据集上进行评估。
1 | def train(lambd): |
- 忽略正则化直接训练
我们现在用 禁用权重衰减后运行这个代码。注意,这里训练误差有了减少,但测试误差没有减少,这意味着出现了严重的过拟合。
1 | train(lambd=0) |
w的L2范数是: 12.837363243103027
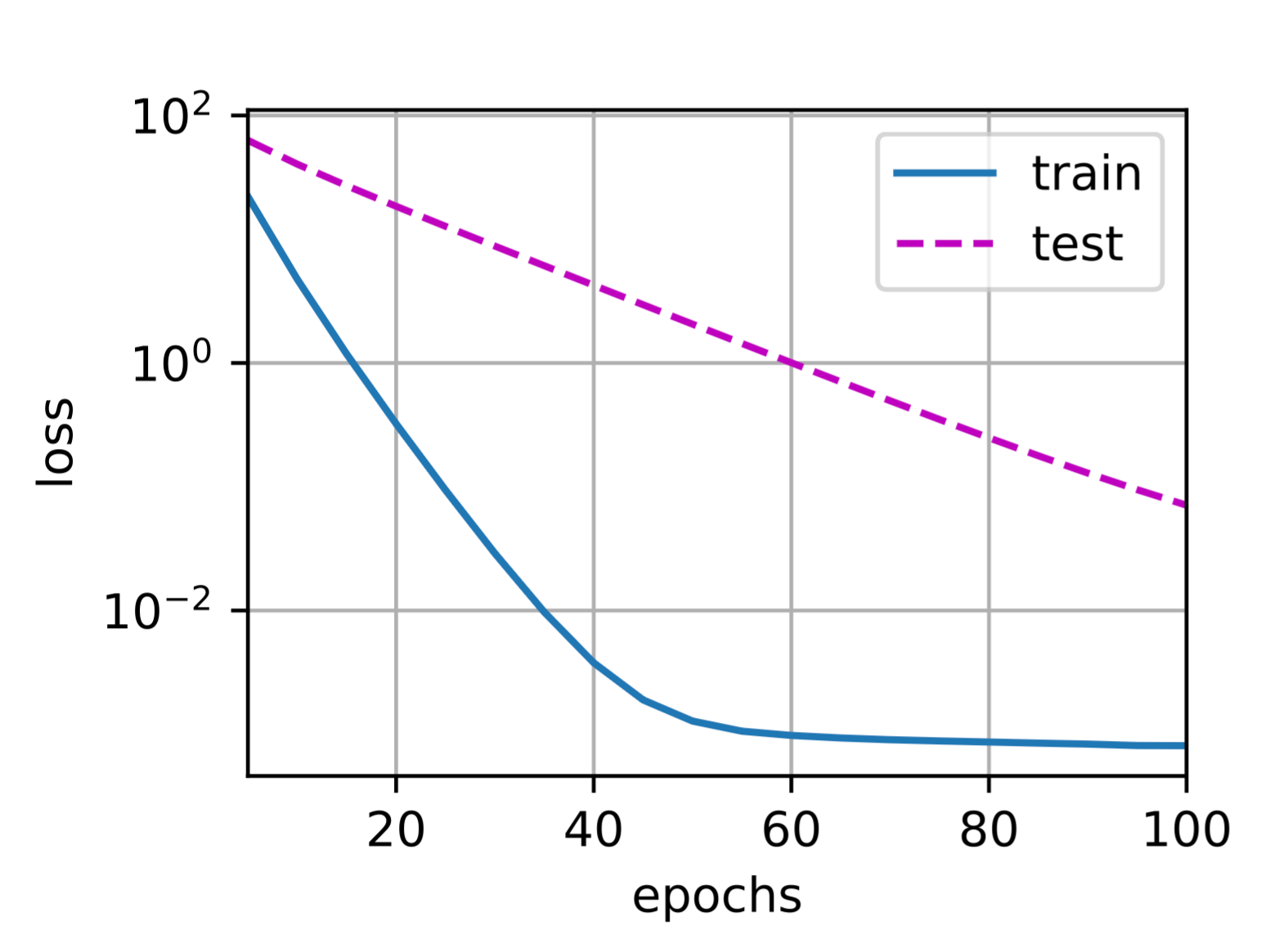 5. 使用权重衰减
5. 使用权重衰减
下面,使用权重衰减来运行代码。注意,在这里训练误差增大,但测试误差减小。这正是期望从正则化中得到的效果。
1 | train(lambd=3) |
w的L2范数是: 0.3454086184501648
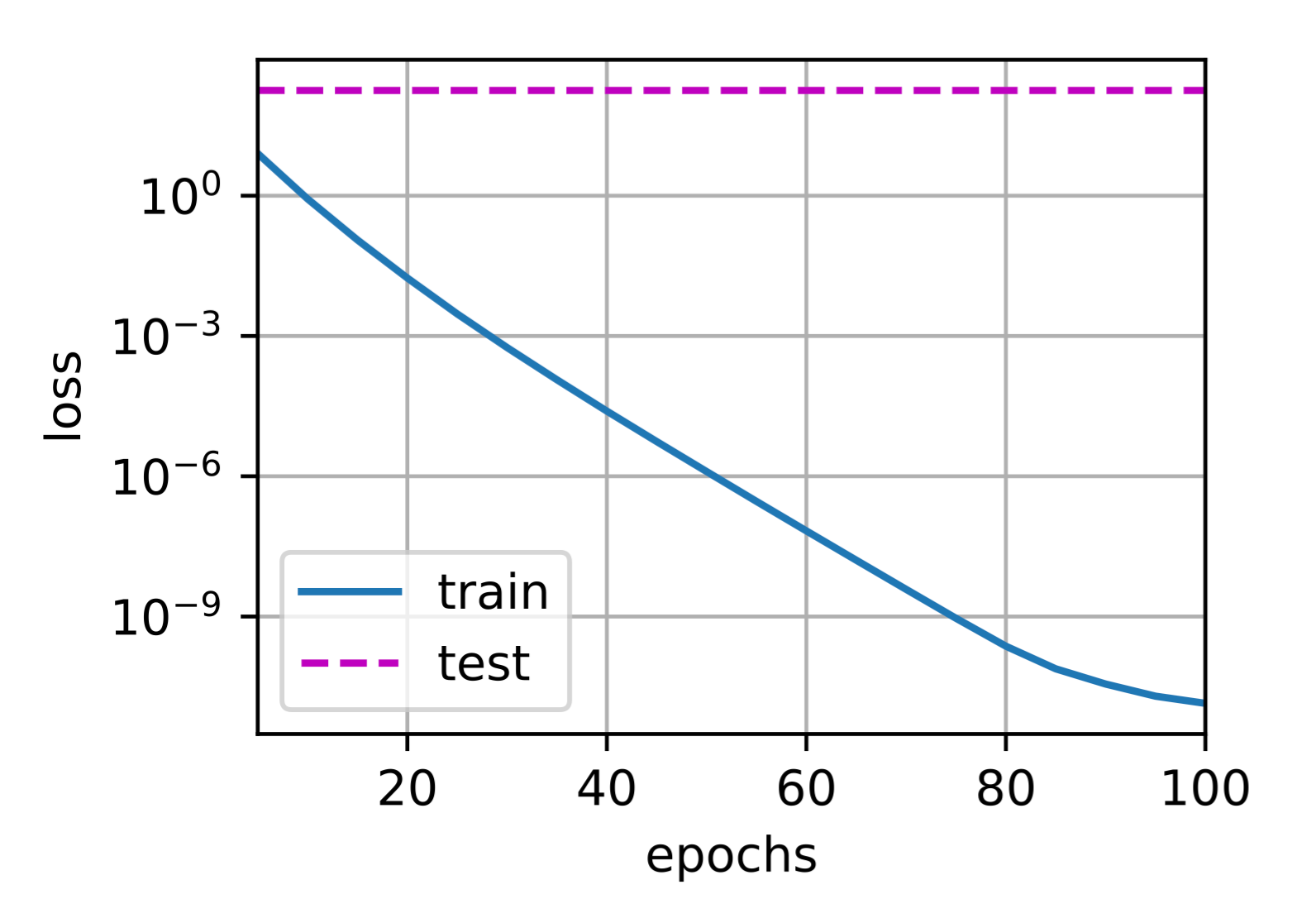 #### 3.4.3.2 简洁实现
#### 3.4.3.2 简洁实现
这里我们只为权重设置了weight_decay,所以偏置参数不会衰减。
1 | def train_concise(wd): |
这些图看起来和我们从零开始实现权重衰减时的图相同然而,它们运行得更快,更容易实现。对于更复杂的问题,这一好处将变得更加明显。
1 | train_concise(0) |
w的L2范数: 13.264945983886719
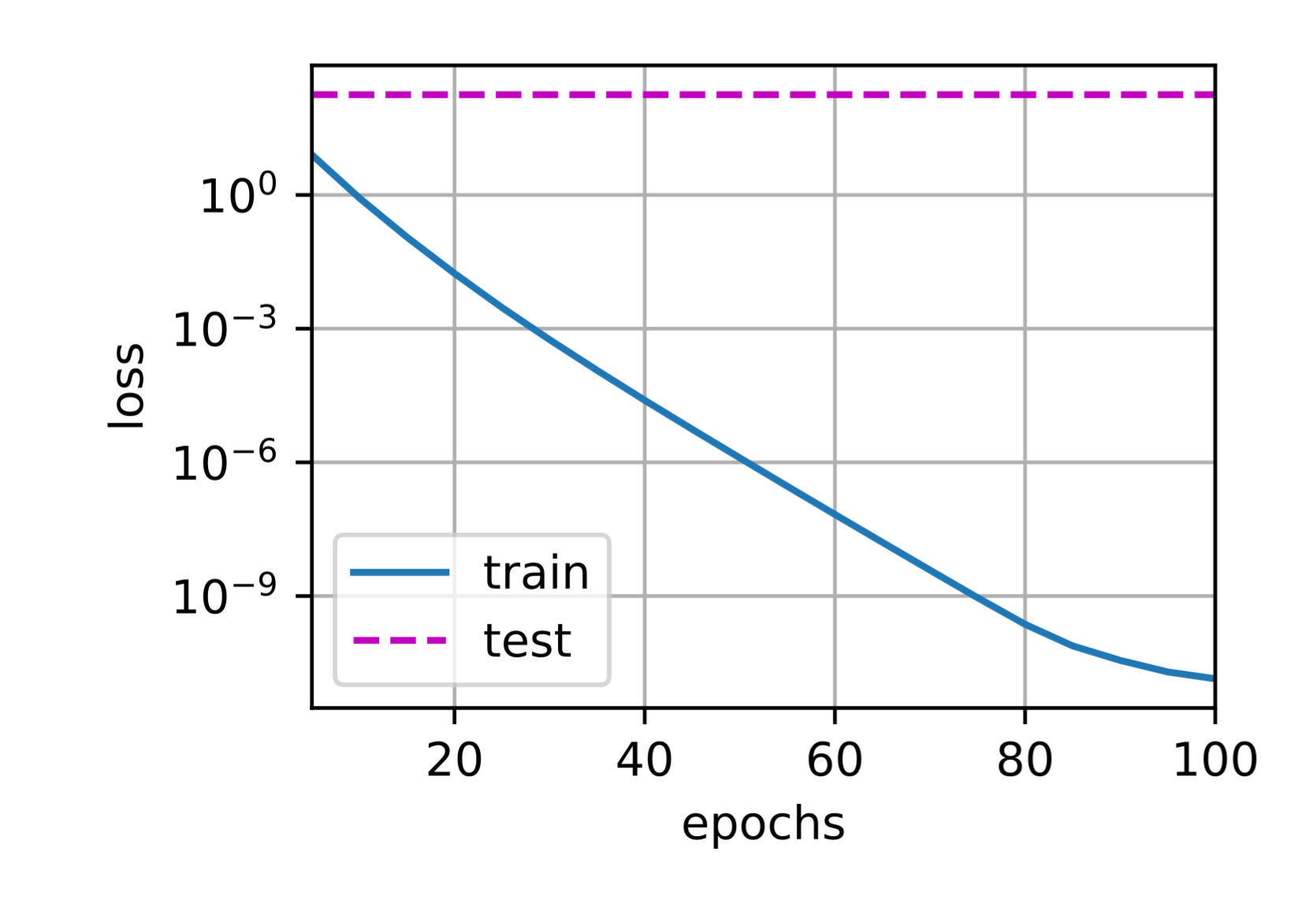
1 | train_concise(3) |
w的L2范数: 0.34366342425346375
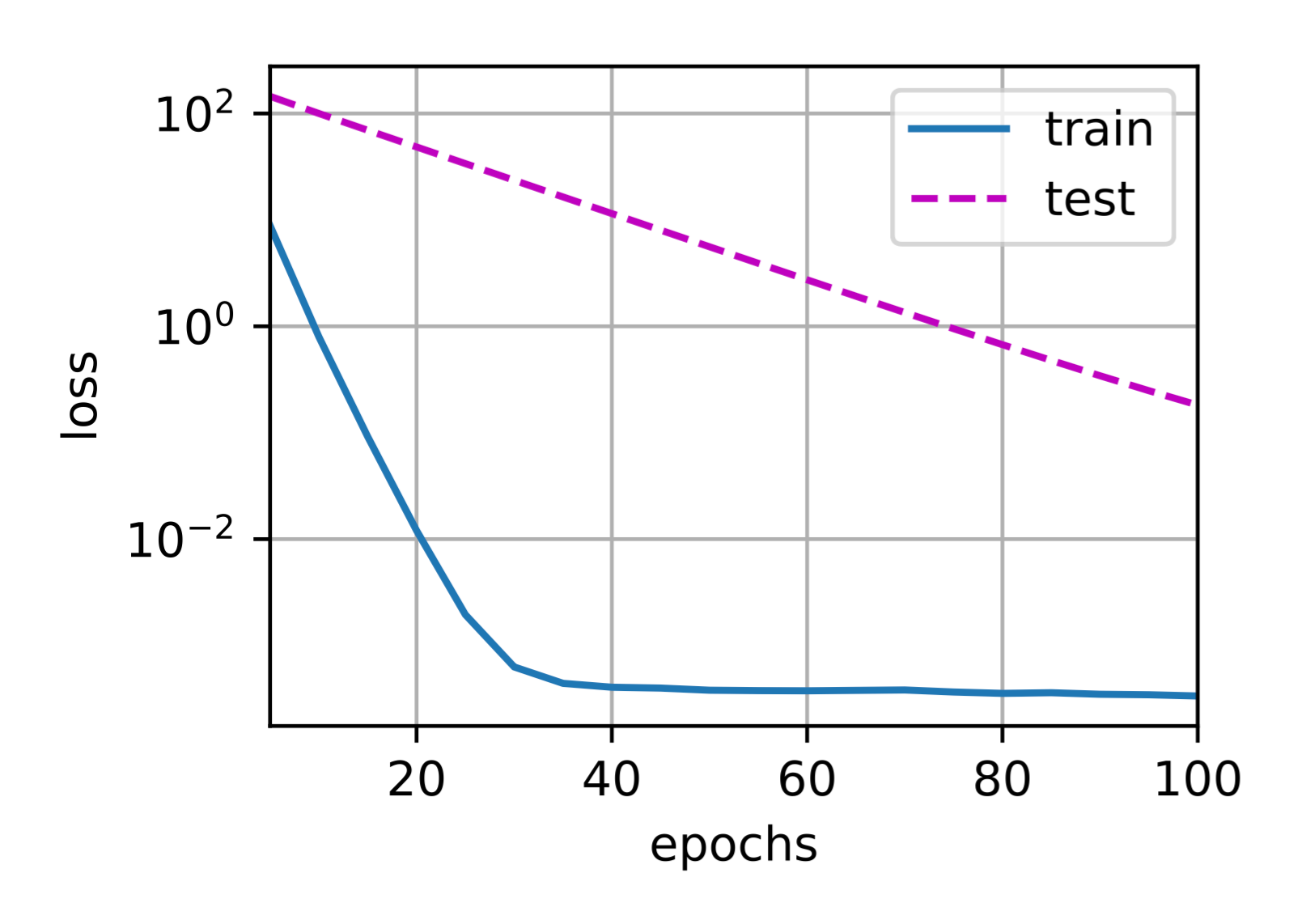
到目前为止,我们只接触到一个简单线性函数的概念。
此外,由什么构成一个简单的非线性函数可能是一个更复杂的问题:
- 例如,再生核希尔伯特空间(RKHS) 允许在非线性环境中应用为线性函数引入的工具。不幸的是,基于RKHS的算法往往难以应用到大型、高维的数据。在这本书中,我们将默认使用简单的启发式方法,即在深层网络的所有层上应用权重衰减。
3.4.4 总结
- 权重衰退通过L2正则项使得模型参数不会过大,从而控制模型复杂度
- 正则项权重 是控制模型复杂度的超参数
- 正则化是处理过拟合的常用方法:在训练集的损失函数中加入惩罚项,以降低学习到的模型的复杂度。
3.5 丢弃法

3.5.1 丢弃法动机、实现及原则
3.5.1.1动机
- 一个好的模型需要对输入数据的扰动鲁棒(健壮性)
如何实现模型的这一能力
-
对 加入噪声得到 ,我们希望:
例:模型的功能是识别猫猫,加入噪音可以是输入模糊的猫猫图片,但尽量不要是狗狗的图片。
-
丢弃法对每个元素进行如下扰动
0 & \text { with probablity } p \
\frac{x_i}{1-p} & \text { otherise }
\end{array}\right.
3.5.1.2 丢弃法使用
- 丢弃法的使用位置
- 通常将丢弃法作用在隐藏全连接层的输出上
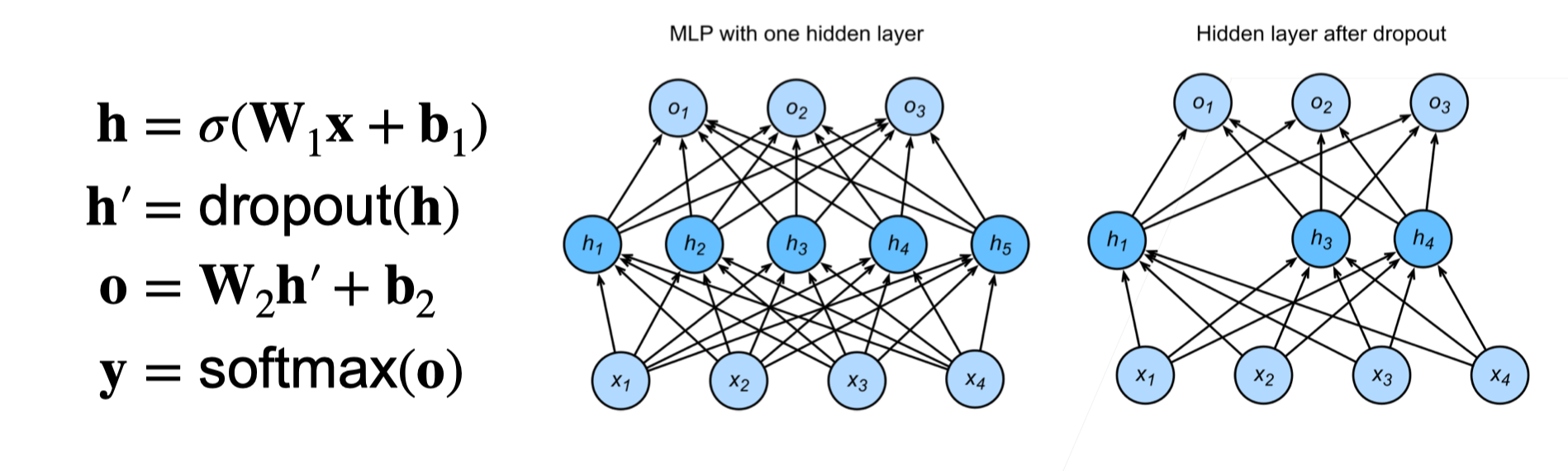
- 随机选中某些神经元将其输出置位 ,因此模型不会过分依赖某些神经元
- 正则项(丢弃法)仅在训练中使用:影响模型参数的更新,预测的时候便不再使用
- 丢弃法将一些输出项随机置0来控制模型复杂度
- 常作用在多层感知机的隐藏层输出上
- 丢弃概率是控制模型复杂度的超参数(常取0.9,0.5,0.1)
3.5.2 代码实现
3.5.2.1 从零实现
要实现单层的暂退法函数,我们从均匀分布中抽取样本,样本数与这层神经网络的维度一致。然后我们保留那些对应样本大于的节点,把剩下的丢弃。
在下面的代码中,我们实现 dropout_layer 函数,
该函数以dropout的概率丢弃张量输入X中的元素,
如上所述重新缩放剩余部分:将剩余部分除以1.0-dropout。
- 定义
dropout_layer
1 | import torch |
我们可以通过下面几个例子来测试dropout_layer函数。我们将输入X通过暂退法操作,暂退概率分别为 0 、0.5 和 1。
1 | X= torch.arange(16, dtype = torch.float32).reshape((2, 8)) |
Results:
1 | tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.], |
- 定义模型参数
定义具有两个隐藏层的多层感知机,每个隐藏层包含256个单元。
1 | num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256 |
- 定义模型
将暂退法应用于每个隐藏层的输出(在激活函数之后),并且可以为每一层分别设置暂退概率:
下面的模型将第一个和第二个隐藏层的暂退概率分别设置为0.2和0.5,并且只在训练期间有效。
1 | dropout1, dropout2 = 0.2, 0.5 |
- 训练和测试
这类似于前面描述的多层感知机训练和测试。
1 | num_epochs, lr, batch_size = 10, 0.5, 256 |
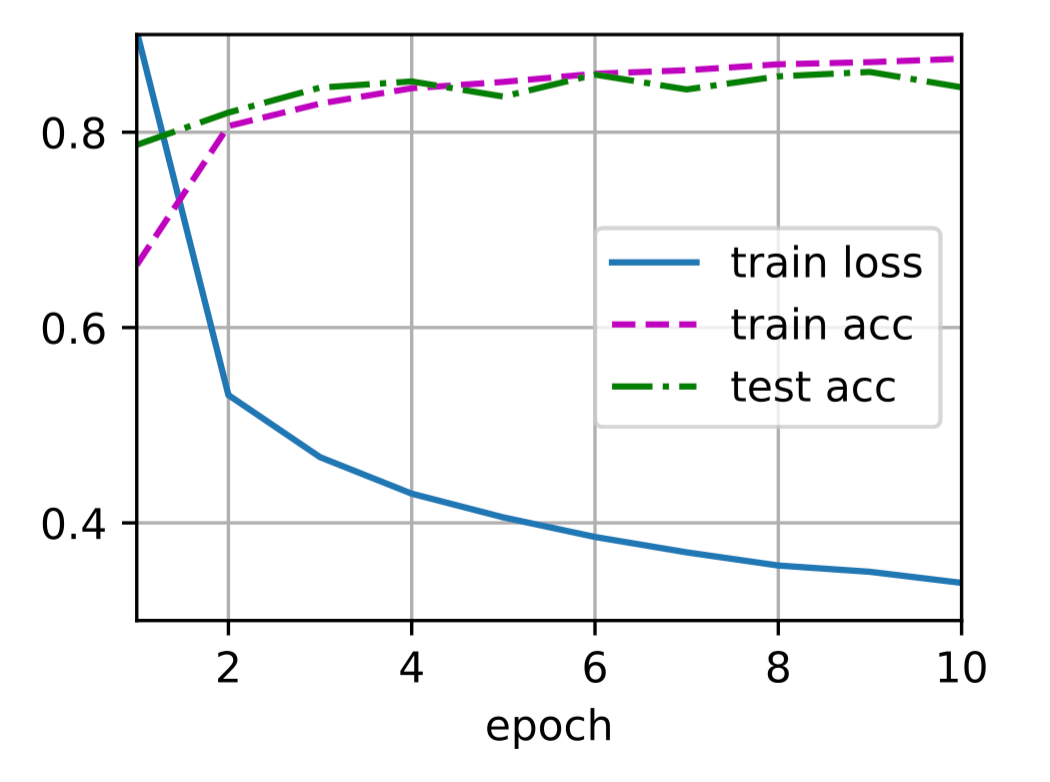 ) #### 3.5.2.2 简洁实现
#### 3.5.2.2 简洁实现
对于深度学习框架的高级 API ,我们只需在每个全连接层之后添加一个Dropout层,将暂退概率作为唯一的参数传递给它的构造函数。
- 训练:
Dropout层将根据指定的暂退概率随机丢弃上一层的输出(相当于下一层的输入)。 - 测试:
Dropout层仅传递数据。
- 配置模型
1 | net = nn.Sequential(nn.Flatten(), |
- 训练和测试
1 | trainer = torch.optim.SGD(net.parameters(), lr=lr) |
Results:
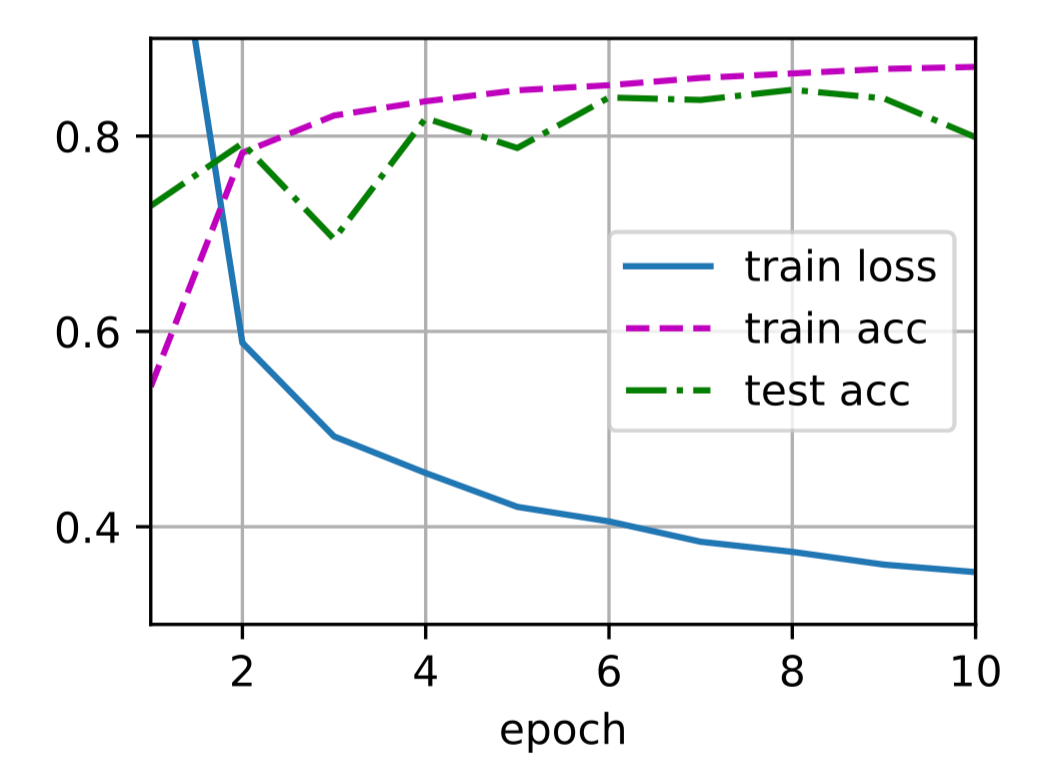
3.5.3 小结
- 暂退法在前向传播过程中,计算每一内部层的同时丢弃一些神经元。
- 暂退法可以避免过拟合,它通常与控制权重向量的维数和大小结合使用的。
- 暂退法将活性值替换为具有期望值的随机变量。
- 暂退法仅在训练期间使用。
3.5.4 Q&A
3.6 数值稳定性
3.6.1 神经网络的梯度
数值稳定性是深度学习中比较重要的点,特别是当神经网络变得很深的时候,数值通常很容易变得不稳定。
 - $t$ 表示层数, $h^{t-1}$ 表示第 $t-1$ 层的输出,经过一个 $f_{t}$ 函数后,得到第 $t$ 层的输出。
- $t$ 表示层数, $h^{t-1}$ 表示第 $t-1$ 层的输出,经过一个 $f_{t}$ 函数后,得到第 $t$ 层的输出。
- 最终输出 的表示:输入 经过若干层( 层)的函数作用,最后被损失函数作用得到输出y。
3.6.1.1 数值稳定性的常见两个问题
- 梯度爆炸
假设梯度都是一些比 大的数比如 ,做 次乘积之后得到 ,这个数字很容易带来一些浮点数上限的问题(需了解更多请参考计算机系统-计算机中浮点数的存储方式)。
- 梯度消失
假设梯度都是一些比 小的数比如 ,做 次乘积之后得到 ,也可能会带来浮点数下溢的问题。
3.6.1.2 例子:MLP
此处我们着重探讨 [[dl-notes-3#3.6.1 神经网络的梯度|神经网络的梯度]] 中所述的求梯度时所做的 d-t 次矩阵乘法,并以一个实例 MLP 来探讨其结果的具体形式。
 - 第一行:定义 $h^{t}$ 和 $h^{t-1}$ (均为向量)的函数关系 $f_{t}$ ,第 $t$ 层的权重矩阵作用于 $t-1$ 层的输出 $h^{t-1}$ 后经过激活函数 $\sigma$ 得到 $h^{t}$ ,注意激活函数 $\sigma$ 逐元素计算。
- 第一行:定义 $h^{t}$ 和 $h^{t-1}$ (均为向量)的函数关系 $f_{t}$ ,第 $t$ 层的权重矩阵作用于 $t-1$ 层的输出 $h^{t-1}$ 后经过激活函数 $\sigma$ 得到 $h^{t}$ ,注意激活函数 $\sigma$ 逐元素计算。
- 第二行:用链导法则,激活函数 先对内部向量逐元素求导,然后把求导后这个向量变成对角矩阵(可以理解为链导法则中内部向量 对自身进行求导,变成一个nxn的对角矩阵,更多请参考邱锡鹏 《神经网络与深度学习》
3.6.1.3 梯度爆炸
- 使用
ReLU作为激活函数
 由于激活函数 `Relu` 求导后或者是1或者是0,变为对角矩阵的斜对角线元素后,与 $W^{i}$ 做乘积,斜对角线为 1 的部分会使得W中元素保留,最终该连乘式中有一些元素来自 $\prod\left ( W^{i} \right )$,如果大部分 $W^{i}$ 中值都大于1,且层数比较大,那么连乘之后可能导致梯度爆炸的问题。
由于激活函数 `Relu` 求导后或者是1或者是0,变为对角矩阵的斜对角线元素后,与 $W^{i}$ 做乘积,斜对角线为 1 的部分会使得W中元素保留,最终该连乘式中有一些元素来自 $\prod\left ( W^{i} \right )$,如果大部分 $W^{i}$ 中值都大于1,且层数比较大,那么连乘之后可能导致梯度爆炸的问题。
- 梯度爆炸问题
- 值超出值域(infinity)
- 对于
16位浮点数尤为严重(数值区间 [6e-5 , 6e4]),GPU用16位浮点数更快
- 对于
- 对学习率敏感
- 如果学习率太大→大参数值→更大的梯度,如此循环几次,容易导致梯度爆炸
- 如果学习率太小→训练无进展
- 我们可能需要在训练过程中不断调整学习率
- 值超出值域(infinity)
3.6.1.4 梯度消失
- 使用
Sigmoid作为激活函数
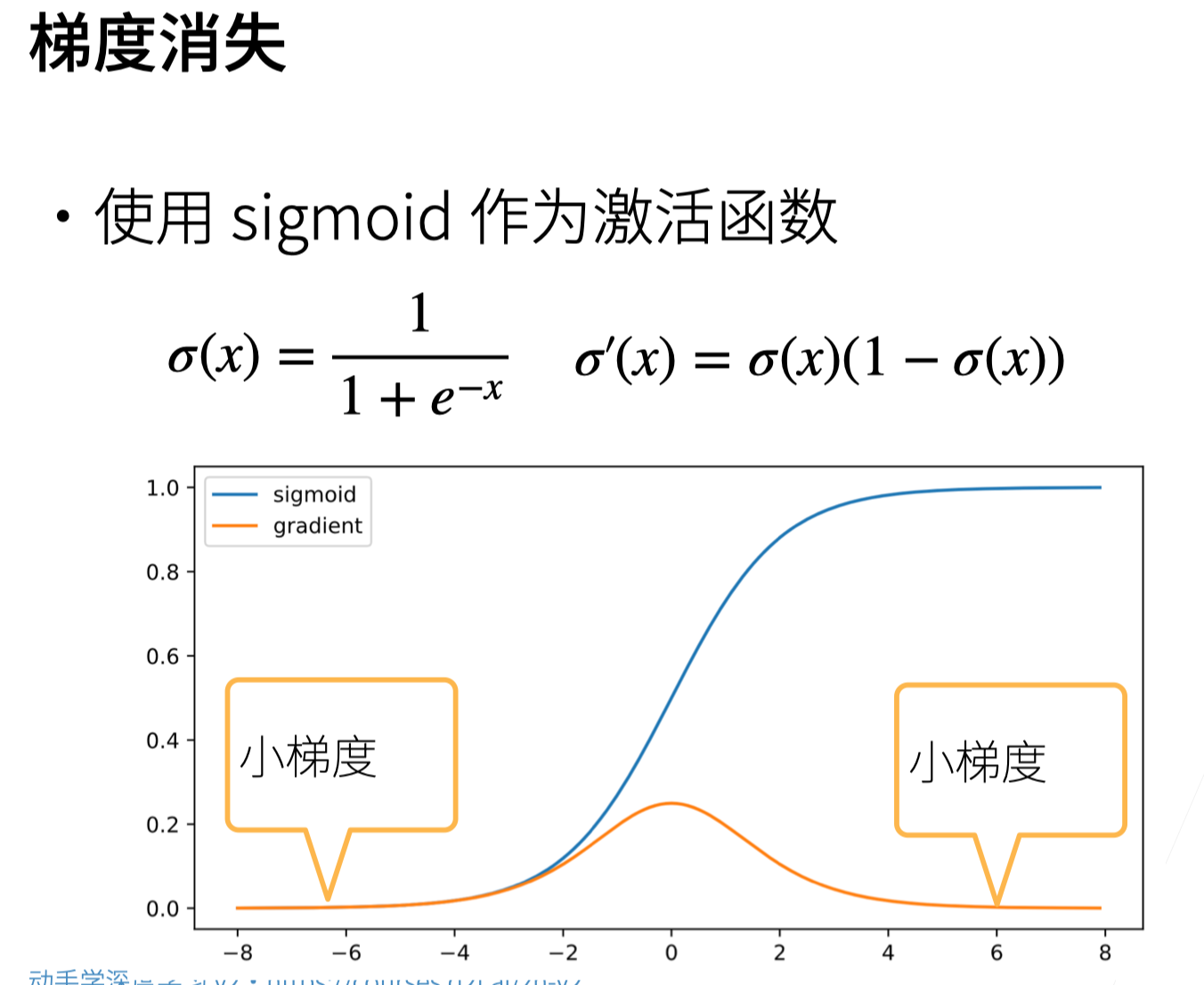 - 蓝色曲线为函数值
- 黄色曲线为梯度,注意到当输入 $x$ 值取 $±6$ 时,此时梯度已经变得很小,由图也可以看出,当输入值稍大或稍小都很容易引起小梯度。
- 蓝色曲线为函数值
- 黄色曲线为梯度,注意到当输入 $x$ 值取 $±6$ 时,此时梯度已经变得很小,由图也可以看出,当输入值稍大或稍小都很容易引起小梯度。
- 梯度消失的问题
- 梯度值变为0
- 对16位浮点数尤为严重
- 训练没有进展
- 不管如何选择学习率,由于梯度已经为0了,学习率x梯度=0
- 对于底部层尤为严重
- 仅仅顶部层训练得较好。第 层导数包含 个矩阵乘积,越往底层走, 越小,乘得越多,梯度消失越严重,所以底部层效果更差。
- 无法让神经网络更深。只能把顶部层训练得比较好,底部层跑不动,这和浅层神经网络没有什么区别。
- 梯度值变为0
3.6.1.5 总结
- 当数值过大或者过小时会导致数值问题
- 常发生在深度模型中,因为其会对 个数累乘
3.6.2 模型初始化和激活函数
3.6.2.1 让训练更加稳定
核心目标:是如何让训练更稳定,梯度值不要太大也不要太小,即让梯度值在合理的范围内(例如 [1e-6, 1e3])。
- 常用方法:
- 将乘法变加法:
ResNet(跳跃连接,如果很多层,加入加法进去)LSTM(引入记忆细胞,更新门,遗忘门,通过门权重求和,控制下一步是否更新)
- 归一化:
- 梯度归一化(归一化均值,方差)
- 梯度裁剪(
clipping):比如大于/小于一个固定的阈值,就让梯度等于这个阈值,将梯度限制在一个范围中。(可以缓解梯度爆炸)
- 合理的权重初始化和激活函数
- 将乘法变加法:
3.6.2.2 让每层的均值/方差是一个常数
-
将每层的输出和梯度都看做随机变量
比如第 层有100维,就将输出和梯度分别看成100个随机变量 -
让它们的均值和方差都保持一致
这样不管神经网络多深,最后一层总与第一层差不多,从而不会梯度爆炸和消失
根据假设,可以列出如下方程式:
 #### 3.6.2.3 权重初始化
#### 3.6.2.3 权重初始化
- 在合理值区间里随机初始参数
- 训练开始的时候更容易有数值不稳定
- 远离最优解的地方损失函数表面可能很复杂
- 最优解附近表面会比较平
- 使用 分布来初始可能对小网络没问题,但不能保证深度神经网络
例子:MLP
下面我们以MLP为例,考虑需要什么条件,才能满足2.2节的假设。
- 模型假设
- 每一层权重中的变量均为独立同分布,并设出均值、方差(, )。
- 每一层输入的变量独立于该层权重变量。同时输入变量之间独立同分布 ( 独立于 )。
- 假设没有激活函数 , 这里 ,可以求得该层输出的期望为0:
- 正向方差
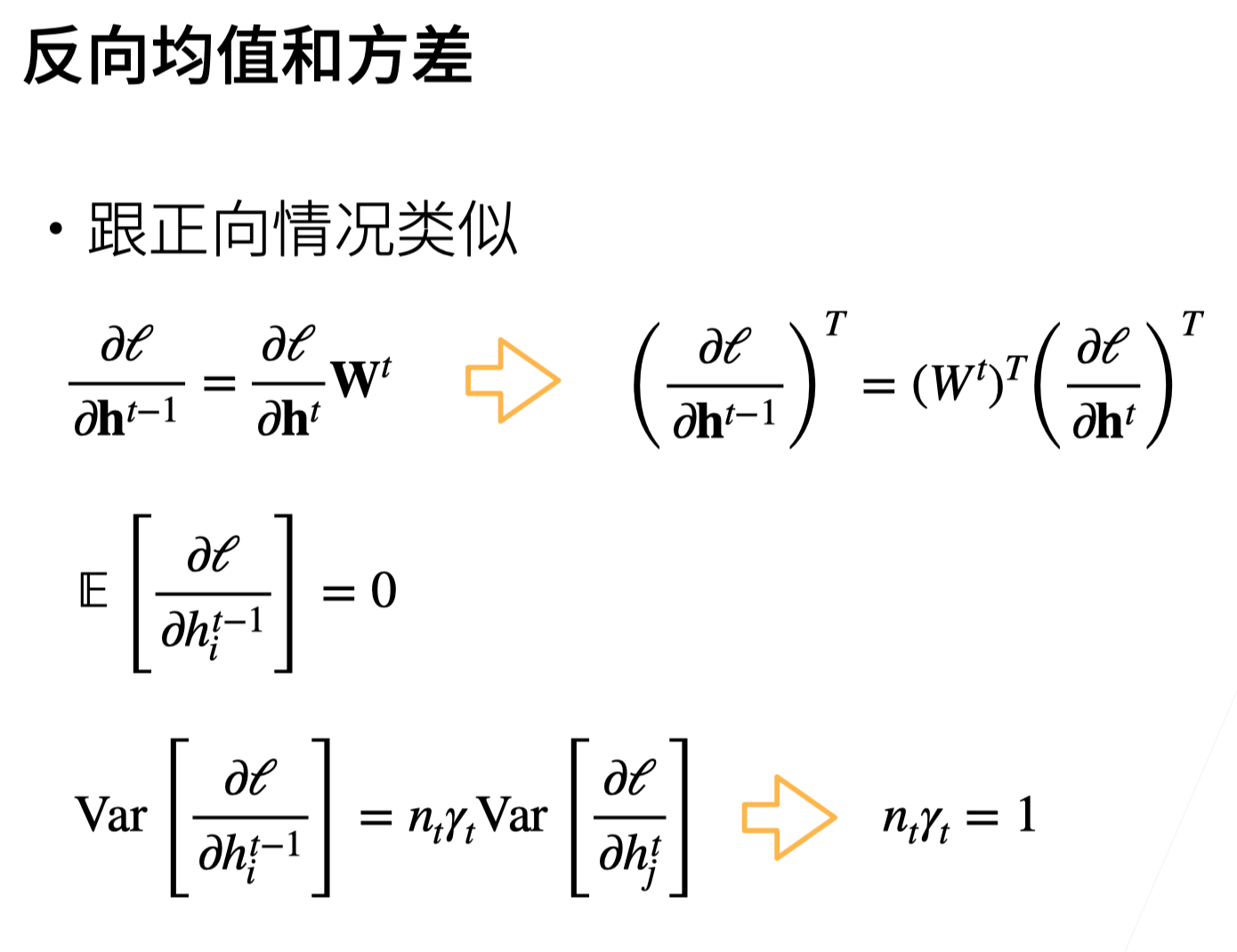
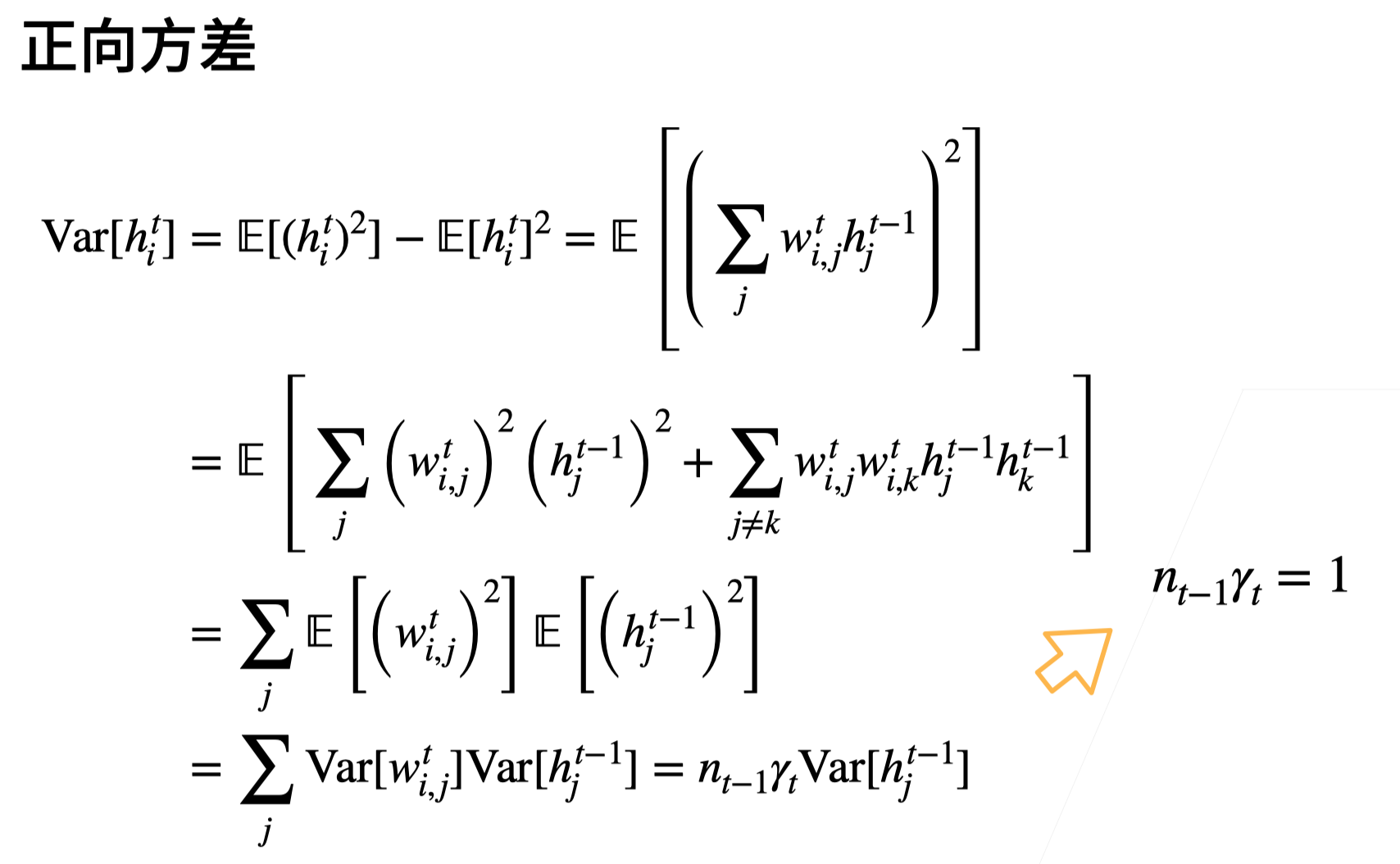 3. 反向均值和方差
3. 反向均值和方差
 4. Xavier初始
4. Xavier初始
 - 上述推导带来的问题:难以同时满足 $n_{t-1}\gamma _{t}=1$ 和 $n_{t}\gamma _{t}=1$。(需要每层输出的维度都相同)
- 上述推导带来的问题:难以同时满足 $n_{t-1}\gamma _{t}=1$ 和 $n_{t}\gamma _{t}=1$。(需要每层输出的维度都相同)
- 采用Xavier折中解决,不能同时满足上面两式,转而满足 上面两式做加法后除以 2 得到的式子,用两种分布进行初始化(每层方差、均值满足推导式)。
- 如果能确定每层输入、输出维度大小,则能确定该层权重的方差大小。
- 权重初始化方式:正态分布、均匀分布,均值/方差满足Xavier的假设。
- 检查常用激活函数
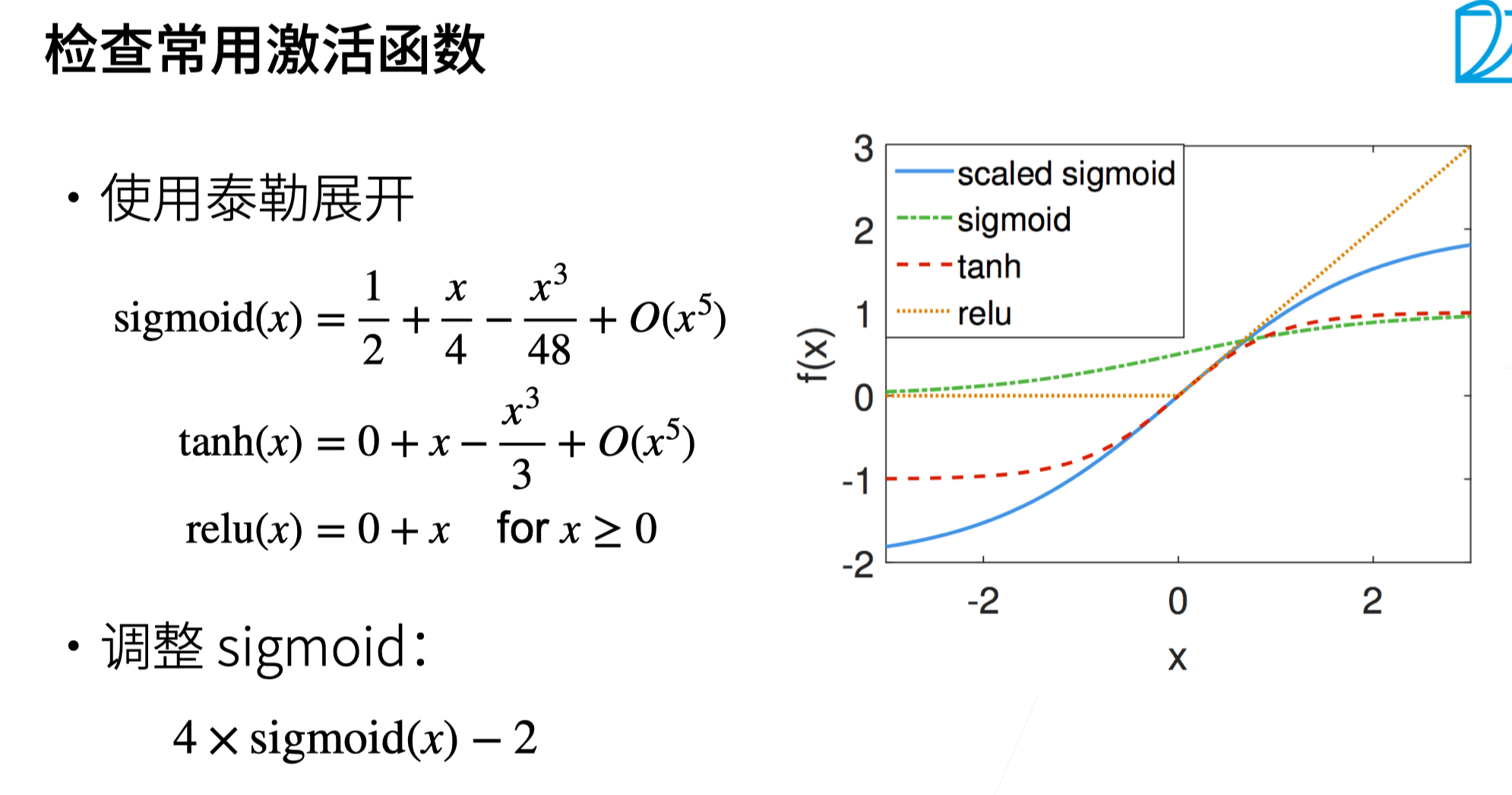 对于常用激活函数: `tanh` , `relu` 满足在零点附近有 $f(x)=x$ ,而 `sigmoid` 函数在零点附近不满足要求,可以对sigmoid函数进行调整(根据 `Taylor` 展开式,调整其过原点)
对于常用激活函数: `tanh` , `relu` 满足在零点附近有 $f(x)=x$ ,而 `sigmoid` 函数在零点附近不满足要求,可以对sigmoid函数进行调整(根据 `Taylor` 展开式,调整其过原点)
3.6.3 总结
- 当数值过大或者过小时,会导致数值问题。
- 常发生在深度模型中,因为其会对n个数累乘。
- 合理的权重初始值(如Xavier)和激活函数的选取(如relu, tanh, 调整后的sigmoid)可以提升数值稳定性。
4.Q&A
问题:nan, inf是怎么产生的以及怎么解决的?
NaN和Inf怎么产生的:参考出现nan、inf原因
如何解决:参考深度学习中nan和inf的解决以及训练网络loss出现Nan解决办法
问题:训练过程中,如果网络层的输出的中间层特征元素的值突然变成nan了,是发生梯度爆炸了吗?
问题:老师,让每层方差是一个常数的方法,您指的是batch normalization吗?想问一下bn层为什么要有伽马和贝塔?去掉可以吗
让每层方差是一个常数,和batch norm没有太多关系
