0%

dive-into-DL-2-Linear

Posted on Edited on In ,
Symbols count in article: 37k Reading time ≈ 33 mins.

0. Preface

本系列博文是 DataWhale 社区 2023年 3月《动手学深度学习（Pytorch）》组队学习活动的笔记，本篇为系列笔记的第二篇—— 线性回归和Softmax回归。

本文是学习李沐老师 B 站视频教程 动手学深度学习 PyTorch版 所记录的笔记。主要使用 Obsidian 软件并借助插件 Meida extended 插件，在 markdown 文件中生成时间戳，可以在后期温习笔记时，方便地定位到原视频所在位置。

原教程视频如下：

PDF 版本笔记见：D2L Note Chapter 2

本次活动面向的人员：

  • 有Python基础
  • 有高数，线代，概率论基础
  • 本科大二左右，或者研一

学习资源整合

  • 教材：Link
  • 纸质书：Link（最低折扣五折购买地址）
  • 视频：Link
  • 笔记：Link
  • 竞赛：Link
  • OpenI云环境（可直接运行）：[Link]）：Link

If we open a quarrel between past and present, we shall find that we have lost the future.
— Winston Churchill

1 线性回归

房价预测例子。00:02 线性回归

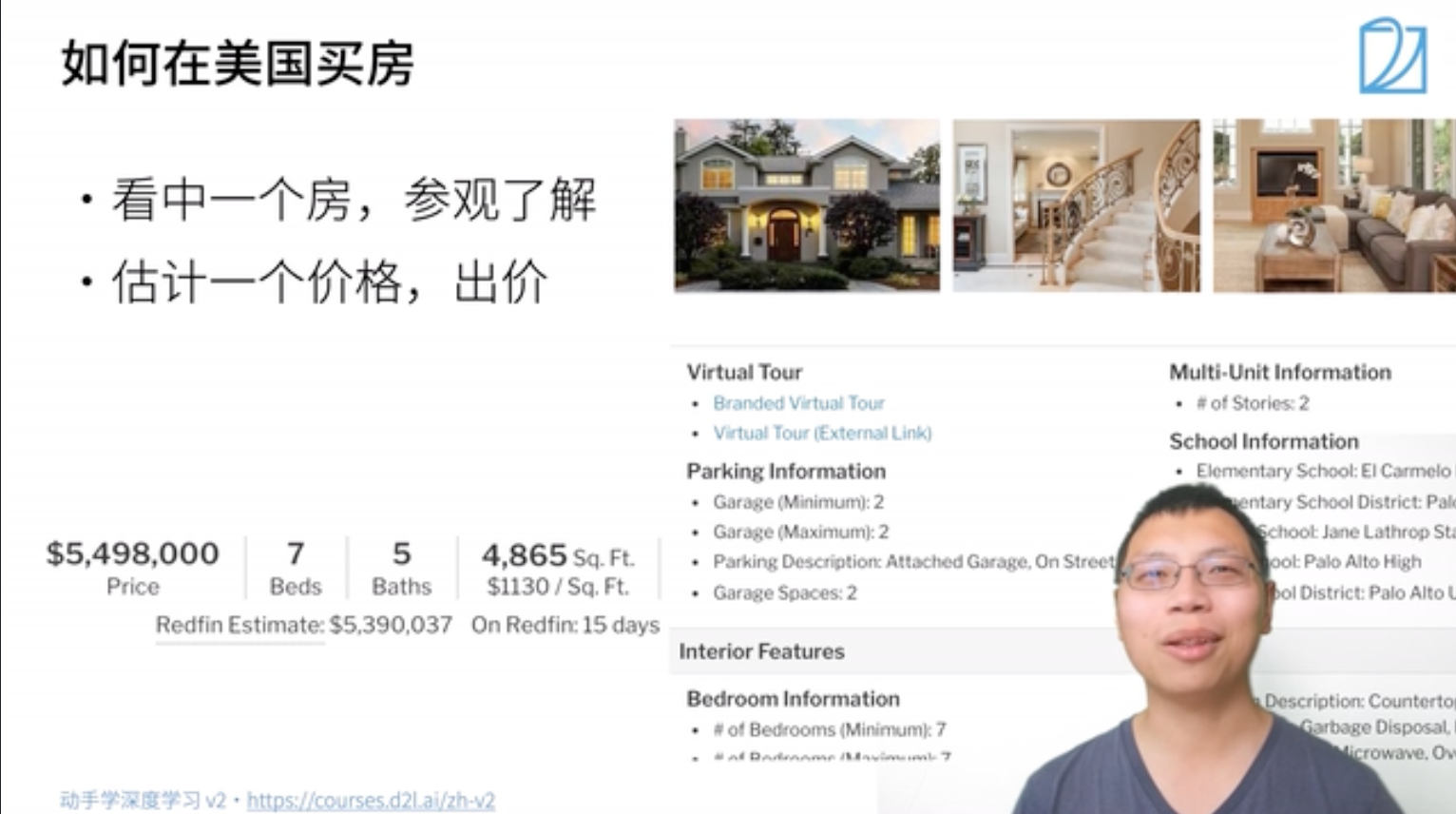
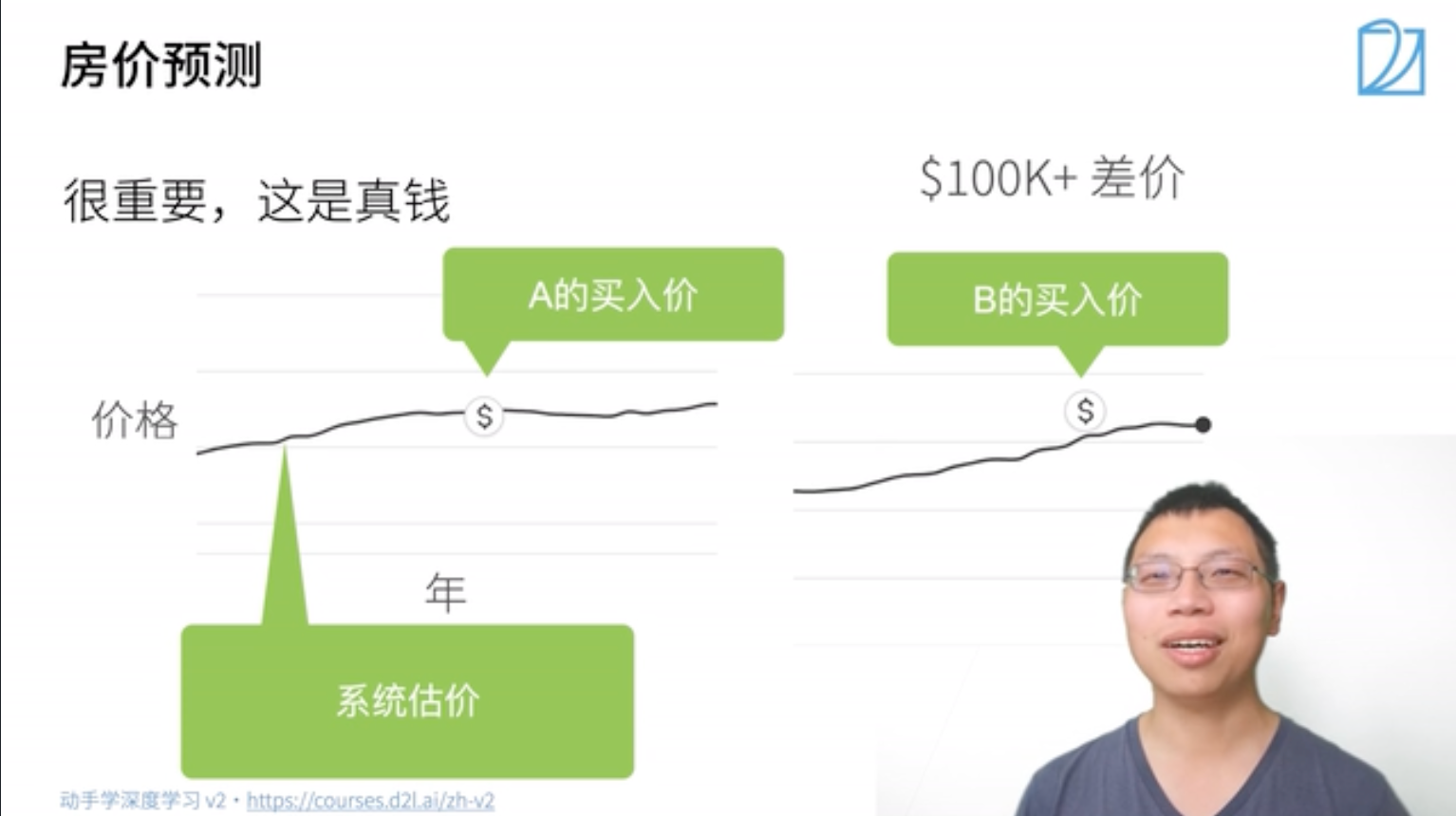**模型简化**。[03:27 模型简化](https://www.bilibili.com/video/BV1PX4y1g7KC?p=1&vd_source=ed04dacb9e3f8845a9f0fa7b8130e4f1&t=207.569903)

  1. 假设一：影响房价的关键因素是卧室个数，卫生间个数和居住面积，记为 x1x_1, x2x_2, x3x_3。

  2. 假设二：成交价是关键因素的加权和

    y=w1x1+w2x2+w3x3+by = w_1 x_1 + w_2 x_2 + w_3 x_3 + b

    权重和偏差的实际值在后文给出。

1.1 线性模型

1.1.1 模型设定

- 输入：$x=[x_1,x_2,...,x_n]^T$

  • 线性模型需要确定一个n维权重和一个标量偏差

    w=[w1,w2,...,wn]T,bw=[w_1,w_2,...,w_n]^T,b

  • 输出 ：

    y=w1x1+w2x2+...+wnxn+by=w_1x_1+w_2 x_2+...+w_nx_n+b

    向量版本的是 y=<w,x>+by=<w,x>+b

Note： 线性模型可以看作是单层神经网络（图片）

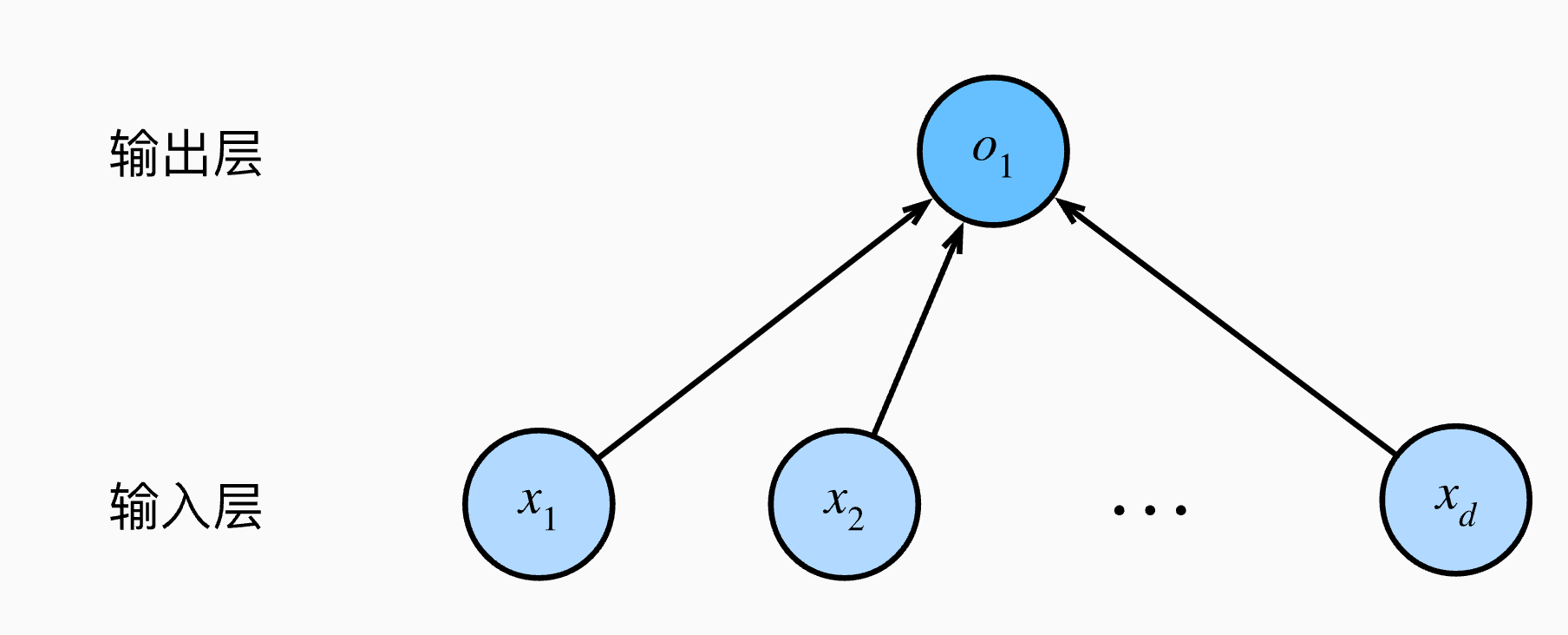神经网络源于神经科学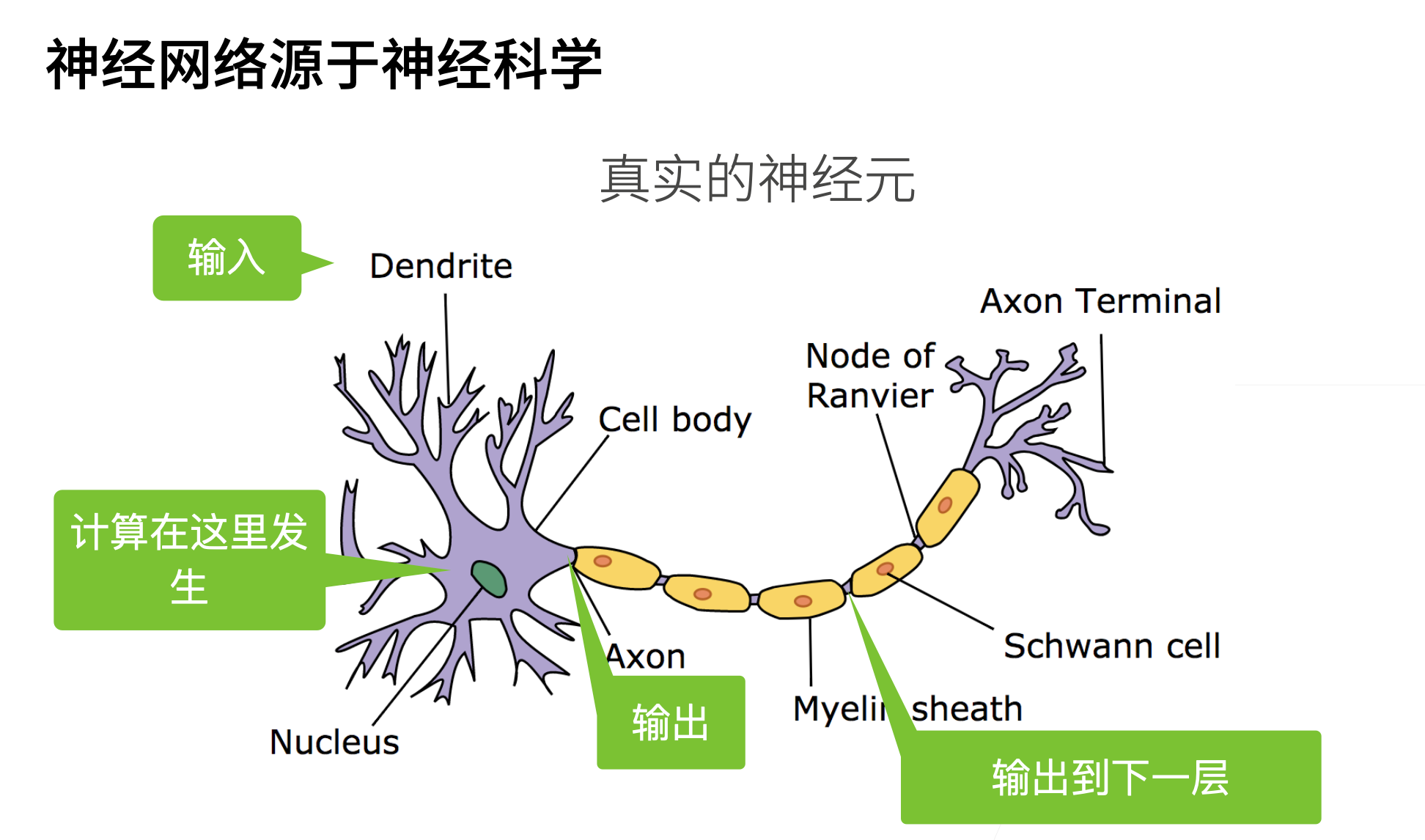： > - 最早的神经网络是源自神经科学的，但是时至今日，很多神经网络已经远远高于神经科学，可解释性也不是很强，不必纠结

1.1.2 衡量估计质量

08:08 评价指标

  • 需要估计模型的预估值和真实值之间的差距，例如房屋售价和股价

  • 假设yy是真实值，y~\tilde{y}是估计值，我们可以比较

    ℓ(y,y~)=12(y−y~)2\ell(y,\tilde{y})=\frac{1}{2}(y-\tilde{y})^2

    这个叫做平方损失

1.1.3 训练数据

  • 收集一些数据点来决定参数值（权重 ω\omega 和偏差 bb），例如6个月内被卖掉的房子。这被称之为训练数据

  • 通常越多越好。

    Note：需要注意的是，现实世界的数据都是有限的，但是为了训练出精确的参数往往需要训练数据越多越好，当训练数据不足的时候，我们还需要进行额外处理。

  • 假设我们有n个样本，记为

    X=[x1,x2,...,xn]T,y=[y1,y2,...yn]TX=[x_1,x_2,...,x_n]^T,y=[y_1,y_2,...y_n]^T

XX的每一行是一个样本，yy的每一行是一个输出的实数值。

1.1.4 参数学习

10:41 参数学习

  • 训练损失。
    训练参数时，需要定义一个损失函数来衡量参数的好坏，应用前文提过的平方损失有公式：
    $$\ell(\mathbf{X}, \mathbf{y},\mathbf{w},b)=\frac{1}{2n}\sum_{i=1}n(y_i-<\mathbf{x}_i,\mathbf{w}>-b)2=\frac{1}{2n}||\mathbf{y}-\mathbf{X} \mathbf{w}-b||^2$$

  • 最小化损失来学习参数。
    训练参数的目的就是使损失函数的值尽可能小（这意味着预估值和真实值更接近）。最后求得的参数值可表示为：

w∗,b∗=arg⁡min⁡w,bl(X,y,w,b)\mathbf{w^*},\mathbf{b}^*=\arg\min_{\mathbf{w},b}l(\mathbf{X},\mathbf{y},\mathbf{w},b)

1.1.5 显示解

12:58 显示解

线性回归有显示解，即可以直接矩阵数学运算，得到参数w和b的最优解，而不是用梯度下降，牛顿法等参数优化方式一点点逼近最优解。

推导过程：

  • 为了方便矩阵表示和计算，将偏差加入权重，X←[X,1]X\gets[X,1], w←[wb]\mathbf{w} \leftarrow\left[\begin{array}{l}\mathbf{w} \\ b\end{array}\right]

ℓ(X,y,w)=12n∥y−Xw∥2∂∂wℓ(X,y,w)=1n(y−Xw)TX\ell(\mathbf{X}, \mathbf{y}, \mathbf{w})=\frac{1}{2 n}\|\mathbf{y}-\mathbf{X w}\|^2 \frac{\partial}{\partial \mathbf{w}} \ell(\mathbf{X}, \mathbf{y}, \mathbf{w})=\frac{1}{n}(\mathbf{y}-\mathbf{X w})^T \mathbf{X}

  • 损失函数是凸函数，最优解满足导数为0，可解出显示解：

    令∂∂ωl(X,y,ω)=0\frac{\partial}{\partial\omega} l(X,y,\omega)=0

    有，1n(y−Xω)TX=0\frac{1}{n}(y-X\omega)^TX=0

    解得：ω∗=(XTX)−1XTy\omega^*=(X^TX)^{-1}X^Ty

1.1.6 总结

  • 线性回归是对 nn 维输入的加权，外加偏差
  • 使用平方损失来衡量预测值和真实值之间的误差
  • 线性回归有显示解
  • 线性回归可以看作单层神经网络

1.2 基础优化算法

00:00 基础优化算法

1.2.1 梯度下降

当模型没有显示解的时候，应用梯度下降法逼近最优解。梯度下降法的具体步骤：

  • 挑选一个初始值 w0w_0，

  • 重复迭代参数，迭代公式为：

    $-\frac{\partial l}{\partial\omega_{t-1}}$ 为函数值下降最快的方向，学习率 $\eta$ 为学习步长。

1.2.2 选择学习率

学习率 η\eta 为学习步长，代表了沿负梯度方向走了多远，这是超参数（人为指定的的值，不是训练得到的）

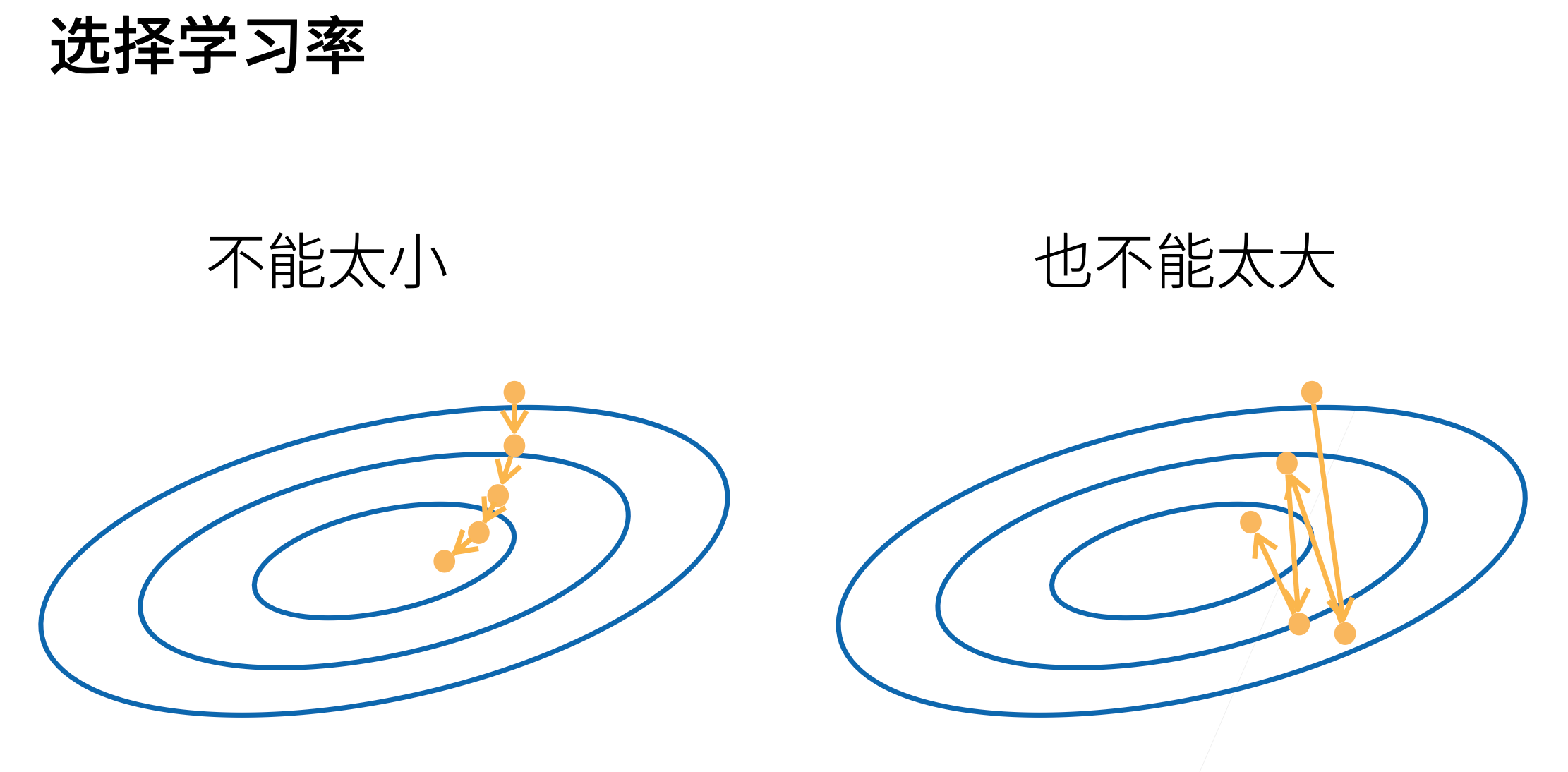- **Note**：学习率不能太大，也不能太小，需要选取适当。

1.2.3 小批量随机梯度下降

04:15 小批量随机梯度下降

在实际应用中，很少直接应用梯度下降法，这是因为在整个训练集上计算梯度代价太大，一个深度神经网络模型可能需要数分钟至数小时。

为了减少运算代价，我们可以 随机采样 bb 个样本i1,i2,...,ibi_1,i_2,...,i_b来近似损失，损失函数为：

\frac{1}{b}\sum_{i\in I_b}l(x_i,y_i,\omega)$$ , 其中 $b$ 是批量大小 `batch size`，也是超参数。 ### 1.2.4 选择批量大小 - $b$ 也不能太大：内存消耗增加；浪费计算资源，一个极端的情况是可能会重复选取很多差不多的样本，浪费计算资源 - $b$ 也不能太小：每次计算量太小，很难以并行，不能最大限度利用 `GPU` 资源 ### 1.2.5 总结 - 梯度下降通过不断**沿着负梯度方向**更新参数求解 - 小批量随机梯度下降是深度学习默认的求解算法（简单，稳定） - **两个重要的超参数：批量大小（batch size），学习率（lr）** ## 1.3 线性回归的从零开始实现 [00:00 代码实现](https://www.bilibili.com/video/BV1PX4y1g7KC?p=3&vd_source=ed04dacb9e3f8845a9f0fa7b8130e4f1&t=0.861988) 在了解线性回归的关键思想之后，可以开始通过代码来动手实现线性回归了。 本节尝试从零开始实现整个方法， 包括数据流水线、模型、损失函数和小批量随机梯度下降优化器。我们将只使用张量和自动求导。 在之后的章节中，会充分利用深度学习框架的优势，介绍更简洁的实现方式。 ### 1.3.1 环境配置 

1
2
3
4
5
!pip install d2l
import numpy as np
import torch
from torch.utils import data 
from d2l import torch as d2l
**Note**：笔者是 `Mac-M1` 系统，需要注意的是，此处推荐使用 `Python 3.9` 环境，如果使用 `3.10` 版本会报如下错误： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
ValueError Traceback (most recent call last)  
Input In [1], in <cell line: 4>()  
1 #import torch  
2 #print(torch.**version**)  
----> 4 from d2l import torch as d2l

... 

---> 13 from pandas._libs.interval import Interval  
14 from pandas._libs.tslibs import (  
15 NaT,  
16 NaTType,  
(...)  
21 iNaT,  
22 )

File pandas/_libs/interval.pyx:1, in init pandas._libs.interval()

ValueError: numpy.ndarray size changed, may indicate binary incompatibility. Expected 96 from C header, got 88 from PyObject
解决办法：重装pandas 
1
pip install --force-reinstall pandas
只需要重新安装 `miniconda` 和 `python` 版本就好，步骤： - 从 [官网](https://docs.conda.io/en/latest/miniconda.html) 下载 `3.9` 版本的 `miniconda`，然后运行： 
1
2
# execute the following at the download location:
sh Miniconda3-py39_23.1.0-1-MacOSX-arm64.sh -b
- 初始化 `miniconda`： 
1
2
# initiate the shell
conda actiavte ~/miniconda3
或者（二选一）： 
1
~/miniconda3/bin/conda init
- 创建虚拟环境 
1
conda create --name d2l python=3.9 -y
- 激活虚拟环境 
1
conda actiavte d2l
- 下载 `torch-gpu` 版本（选） 考虑到后续可能需要 `gpu` 加速训练，因此此处直接下载 `torch-gpu` 版本。 
1
pip install --pre torch torchvision torchaudio --extra-index-url https://download.pytorch.org/whl/nightly/cpu
**Note**：检查是否安装成功，首先在命令行输入 `python` 进入 `python` 编程环境，然后输入 
1
2
3
4
>>> import torch  
>>> print(torch.backends.mps.is_available())

True
若输出结果为 `Ture`，则表明安装成功。 - 下载 `ipykernel` 考虑到书中给的代码运行环境是 `jupyter`，应该此处安装 `ipykernel`，以确保 `jupyter-notebook` 中可以使用刚刚安装的 `d2l` 虚拟环境的内核。 
1
2
3
pip install ipykernel

python -m ipykernel install --user --name ENVNAME --display-name DISP_NAME
**Note**：`ENVNAME` 和 `DISP-NAME` 分别为虚拟环境的名字 （此处为 `d2l`）和想要显示的名字。为了简便，此处将两个字段都设置为 `d2l`。 ### 1.3.2 生成数据集 为了简单起见，我们将**根据带有噪声的线性模型构造一个人造数据集**。 任务：使用这个有限样本的数据集来恢复这个模型的参数。 我们将使用低维数据，这样可以很容易地将其可视化。 在下面的代码中，我们生成一个包含 $1000$ 个样本的数据集， 每个样本包含从标准正态分布中采样的 $2$ 个特征。 我们的合成数据集是一个矩阵 $\mathbf{X}\in \mathbb{R}^{1000 \times 2}$。 使用线性模型参数 $\mathbf{w} = [2, -3.4]^\top$、$b = 4.2$ 和噪声项 $\epsilon$ 生成数据集及其标签： $$\mathbf{y}= \mathbf{X} \mathbf{w} + b + \mathbf\epsilon$$. 可以将 $\epsilon$ 视为模型预测和标签时的潜在观测误差。 在这里我们认为标准假设成立，即 $\epsilon$ 服从均值为 $0$ 的正态分布。 为了简化问题，我们将标准差设为 $0.01$。 下面的代码生成合成数据集。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def synthetic_data(w, b, num_examples):  #@save
    """
    生成y=Xw+b+噪声
    @para w 权重
    @para b 偏差 
    @para num_examples 样本数量
    @return
        X 随机生成的特征数据，(num_examples, len(w))
        y X对应的标签 （num_examples，1）
    
    """
    X = torch.normal(0, 1, (num_examples, len(w)))#生成均值为0，方差为1，数据维度是（num_examples, len(w)）的随机数据作为训练样本
    y = torch.matmul(X, w) + b #生成X对应的预测值y
    y += torch.normal(0, 0.01, y.shape)# 加入噪音，加入的是均值为0，方差为0.01，纬度和y.shape一致的噪音进行干扰
    return X, y.reshape((-1, 1))#返回X，y，y为列向量
1
2
3
true_w = torch.tensor([2, -3.4]) #真实权重
true_b = 4.2 #真实偏差
features, labels = synthetic_data(true_w, true_b, 1000) #随机生成1000组训练数据及标签
**注意**：`features`中的每一行都包含一个二维数据样本，`labels`中的每一行都包含一维标签值（一个标量）。 
1
2
3
4
>>> print('features:', features[0],'\nlabel:', labels[0]) #打印一个样本数据和对应标签

features: tensor([-1.1678, -0.7740]) 
label: tensor([4.5072])
通过生成第二个特征`features[:, 1]`和`labels`的散点图，可以直观观察到两者之间的线性关系。 
1
2
3
#可视化数据
d2l.set_figsize() 
d2l.plt.scatter(features[:, (1)].detach().numpy(), labels.detach().numpy(), 1); #x轴为features的第一列，y轴为标签值，正相关
Results: <img src="https://cdn.jsdelivr.net/gh/YangSuoly/Images/dl-notes/202303182223495.png" style="zoom:67%;" /> ### 1.3.3 读取数据集 训练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用它们来更新我们的模型。由于这个过程是训练机器学习算法的基础，所以有必要定义一个函数，该函数能打乱数据集中的样本并以小批量方式获取数据。 在下面的代码中，**定义了一个`data_iter`函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为`batch_size`的小批量**。 每个小批量包含一组特征和标签。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def data_iter(batch_size, features, labels):
    """
    随机获取一小批样本的数据
    @para batch_size 批量的大小
    @para features 训练数据
    @para labels 训练数据对应的标签
    @return
        迭代器，每次返回batch_size大小的两组数据，一个是训练样本，一个是对应的标签   
        
    """
    num_examples = len(features) #获取样本大小
    indices = list(range(num_examples)) #获取样本脚标的list
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices) #随机变换indices
    for i in range(0, num_examples, batch_size): #开始循环
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)]) #有可能不能整除，取i + batch_size和num_examples的较小值
        yield features[batch_indices], labels[batch_indices] #相当于是一个迭代器，每次返回batch_size个样本
通常，我们利用 `GPU` 并行运算的优势，处理合理大小的“小批量”。每个样本都可以并行地进行模型计算，且每个样本损失函数的梯度也可以被并行计算。`GPU` 可以在处理几百个样本时，所花费的时间不比处理一个样本时多太多。 我们直观感受一下小批量运算：读取第一个小批量数据样本并打印。每个批量的特征维度显示批量大小和输入特征数。同样的，批量的标签形状与`batch_size`相等。 
1
2
3
4
5
batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y) #X为10 x 2的tensor，y为10 x 1的tensor
    break
tensor([[ 0.6301, -0.3610], [-1.0436, -0.4737], [-0.2955, 0.2614], [-0.1482, -0.0150], [-0.7068, 1.1198], [ 1.3959, 0.2696], [ 0.9270, 0.1575], [-0.6020, 0.4045], [-1.8370, 0.6234], [ 0.1756, 0.0142]]) tensor([[ 6.6870], [ 3.7135], [ 2.7083], [ 3.9501], [-1.0375], [ 6.0819], [ 5.5011], [ 1.6290], [-1.5751], [ 4.5169]]) 当我们运行迭代时，我们会连续地获得不同的小批量，直至遍历完整个数据集。上面实现的迭代对于教学来说很好，但它的执行效率很低，可能会在实际问题上陷入麻烦。 例如，它要求我们将所有数据加载到内存中，并执行大量的随机内存访问。在深度学习框架中实现的内置迭代器效率要高得多，它可以处理存储在文件中的数据和数据流提供的数据。 ### 1.3.4 初始化模型参数 在我们开始用小批量随机梯度下降优化我们的模型参数之前，需要先有一些参数。 在下面的代码中，我们通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重，并将偏置初始化为0。 
1
2
3
# 由于训练的时候需要更细参数，计算梯度，所以requires_grad=True
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True) #w初始化为均值为0，方差为0.001的符合正态分布的数组，纬度为2 x1
b = torch.zeros(1, requires_grad=True) #b初始化为0，纬度为1，就是一个实数
在初始化参数之后，需要更新这些参数，直到这些参数足够拟合我们的数据。 每次更新都需要计算损失函数关于模型参数的梯度。有了这个梯度，我们就可以向减小损失的方向更新每个参数。 因为手动计算梯度很枯燥而且容易出错，所以没有人会手动计算梯度。我们引入自动微分来计算梯度。 ### 1.3.5 定义模型 接下来，我们必须 **定义模型，将模型的输入和参数同模型的输出关联起来。** 回想一下，要计算线性模型的输出， 我们只需计算输入特征$\mathbf{X}$和模型权重$\mathbf{w}$的矩阵-向量乘法后加上偏置$b$。 注意，上面的$\mathbf{Xw}$是一个向量，而$b$是一个标量。 回想一下 [[dl-notes-1#广播机制|数据操作与数据预处理]] 中描述的广播机制： 当我们用一个向量加一个标量时，标量会被加到向量的每个分量上。 
1
2
3
4
5
6
7
8
9
10
11
def linreg(X, w, b):  #@save
    """
    线性回归模型
    @para X 训练数据（num_examples,len(w)）
    @para w 权重 （2，1）
    @para b 偏差 实数
    @return
        模型的预估值
    
    """
    return torch.matmul(X, w) + b
### 1.3.6 定义损失函数 因为需要计算损失函数的梯度，所以我们应该先定义损失函数。这里使用 [[dl-notes-1#2.1 线性回归|线性回归]] 中描述的平方损失函数。 **Note**：在实现中，我们需要将真实值`y`的形状转换为和预测值`y_hat`的形状相同。 
1
2
3
4
5
6
7
8
9
def squared_loss(y_hat, y):  #@save
    """
    均方损失
    @para y_hat 训练数据的真实值（num，1）
    @para y 训练数据的预测值
    @return
        均方误差，没有除以样本数目 (batch_size,1)
    """
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
### 1.3.7 定义优化算法 正如我们在 [[dl-notes-1#2.1 线性回归|线性回归]] 中讨论的，尽管线性回归有解析解，但本书中的其他模型却没有。这里我们介绍小批量随机梯度下降。 - 在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。 - 接下来，朝着减少损失的方向更新我们的参数。 下面的函数实现小批量随机梯度下降更新。该函数接受模型参数集合、学习速率和批量大小作为输入。每一步更新的大小由学习速率`lr`决定。因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（`batch_size`）来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。 
1
2
3
4
5
6
7
8
9
10
11
12
def sgd(params, lr, batch_size):  #@save
    """
    小批量随机梯度下降
    @para params 参数
    @para lr 学习率，人为指定
    @para batch_size 批量大小
    @return 
    """
    with torch.no_grad(): #不需要计算梯度
        for param in params:
            param -= lr * param.grad / batch_size #梯度下降法更新参数
            param.grad.zero_() #手动梯度归零
### 1.3.8 训练 现在我们已经准备好了模型训练所有需要的要素，可以实现主要的 **训练过程** 部分了。 理解这段代码至关重要，因为从事深度学习后， 你会一遍又一遍地看到几乎相同的训练过程。 在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。 计算完损失后，我们开始反向传播，存储每个参数的梯度。 最后，我们调用优化算法`sgd`来更新模型参数。 概括一下，我们将执行以下循环： * 初始化参数 * 重复以下训练，直到完成 * 计算梯度 $\mathbf{g} \leftarrow \partial_{(\mathbf{w},b)} \frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} l(\mathbf{x}^{(i)}, y^{(i)}, \mathbf{w}, b)$ * 更新参数$(\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \eta \mathbf{g}$ 在每个*迭代周期*（epoch）中，我们使用`data_iter`函数遍历整个数据集， 并将训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。 这里的迭代周期个数`num_epochs`和学习率`lr`都是超参数，分别设为3和0.03。 设置超参数很棘手，需要通过反复试验进行调整。 我们现在忽略这些细节，以后会在 :numref:`chap_optimization`中详细介绍。 
1
2
3
4
lr = 0.003 #学习率
num_epochs = 3 #训练次数
net = linreg #网络，之前定义的线性网络
loss = squared_loss #损失函数，之前定义的平方损失函数
1
2
3
4
5
6
7
8
9
10
11
#开始训练
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels) #计算所有样本的损失函数
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
epoch 1, loss 9.117679 epoch 2, loss 4.993863 epoch 3, loss 2.736007 因为我们使用的是自己合成的数据集，所以我们知道真正的参数是什么。因此，可以通过 **比较真实参数和通过训练学到的参数来评估训练的成功程度**。 
1
2
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
Results: 
1
2
3
w的估计误差: tensor([ 0.7622, -1.4047], grad_fn=<SubBackward0>)
b的估计误差: tensor([1.7077], grad_fn=<RsubBackward1>)

可以发现，真实参数和通过训练学到的参数确实非常接近。 **注**：我们不应该想当然地认为能够完美地求解参数。在机器学习中，我们通常不太关心恢复真正的参数，而更关心如何高度准确预测参数。幸运的是，即使是在复杂的优化问题上，随机梯度下降通常也能找到非常好的解。其中一个原因是，在深度网络中存在许多参数组合能够实现高度精确的预测。 ### 1.3.9 小结 * 我们学习了深度网络是如何实现和优化的。在这一过程中只使用张量和自动微分，不需要定义层或复杂的优化器。 * 这一节只触及到了表面知识。在下面的部分中，我们将基于刚刚介绍的概念描述其他模型，并学习如何更简洁地实现其他模型。 ## 1.4 调用 API 实现 [00:00 简洁实现](https://www.bilibili.com/video/BV1PX4y1g7KC?p=4&vd_source=ed04dacb9e3f8845a9f0fa7b8130e4f1&t=0.743043) 在上一节中，我们只运用了： 1. 通过张量来进行数据存储和线性代数； 2. 通过自动微分来计算梯度。 实际上，由于数据迭代器、损失函数、优化器和神经网络层很常用，现代深度学习库也为我们实现了这些组件。 在本节中，将介绍如何通过使用深度学习框架来简洁地实现线性回归模型。 ### 1.4.1 生成数据 
1
2
3
4
5
6
7

true_w = torch.tensor([2, -3.4]) # 真实权重
true_b = 4.2 # 真实偏差
features, labels = d2l.synthetic_data(true_w, true_b, 1000) 
# 应用liner-regression-concise里面的函数，生成训练数据

features
Results: 
1
2
3
4
5
6
7
tensor([[-1.4684,  0.0977],
		[ 1.7930,  0.9657],
		[ 1.1813,  2.1203],
		...,
		[ 0.0698,  0.6992],
		[-1.6323,  2.0169],
		[-0.4198, -1.1236]])
### 1.4.2 读取数据集 可以 **调用框架中现有的API来读取数据** 。 我们将 `features` 和 `labels` 作为 `API` 的参数传递，并通过数据迭代器指定 `batch_size`。 此外，布尔值 `is_train` 表示是否希望数据迭代器对象在每个迭代周期内打乱数据。 
1
2
3
4
5
6
7
8
9
10
11
def load_array(data_arrays, batch_size, is_train=True):  #@save
    """
    构造一个PyTorch数据迭代器
    @para data_arrays 训练数据
    @para batch_size 批量大小
    @para is_train=True 是否训练，选择True会随机选择数据
    @return
        迭代器，每次返回batch_size大小的两组数据，一个是训练样本，一个是对应的标签 
    """
    dataset = data.TensorDataset(*data_arrays) #数据集
    return data.DataLoader(dataset, batch_size, shuffle=is_train)
**Note**: dataloader可以理解为数据的一个接口，说明见 [PyTorch中的Data.DataLoader](https://blog.csdn.net/lipengfei0427/article/details/109547241)， - 其构造函数为： 
1
2
3
class torch.utils.data.DataLoader(dataset, batch_size=1, shuffle=False, sampler=None,
	batch_sampler=None, num_workers=0, collate_fn=<function default_collate>, 
	pin_memory=False,drop_last=False, timeout=0, worker_init_fn=None)
- `DataLoader` 的参数说明： - `dataset (Dataset)`：定义要加载的数据集； - `batch_size (int, optional)`：`定义batch_size` 大小，也就是一次加载样本的数量，默认是 `1`； - `shuffle (bool, optional)`：在每个epoch开始的时候，是否进行数据重排序，默认 `False`； - `sampler (Sampler, optional)`：定义从数据集中取样本的策略，如果进行了指定，那么 `shuffle` 必须是 `False`。 - `num_workers (int, optional)`：定义加载数据使用的进程数，`0` 代表所有的数据都被装载进主进程，默认是 `0`。 - `drop_last (bool, optional)`： 这个是对最后的未完成的batch来说的，比如你的 `batch_size` 设置为 `64`，`而一个epoch` 只有 `100` 个样本，`如果设置为True`，那么训练的时候后面的 `36` 个就被扔掉了。如果为 `False`（默认），那么会继续正常执行，只是最后的 `batch_size` 会小一点。 `Dataloader` 的处理逻辑是先通过 `Dataset` 类里面的 `__getitem__` 函数获取单个的数据，然后组合成batch，再使用collate_fn所指定的函数对这个batch做一些操作 
1
2
batch_size = 10 # 批量大小
data_iter = load_array((features, labels), batch_size) # 随机返回的数据
使用`data_iter`的方式与我们在 :numref:`sec_linear_scratch`中使用`data_iter`函数的方式相同。为了验证是否正常工作，让我们读取并打印第一个小批量样本。 与 :numref:`sec_linear_scratch`不同，这里我们使用`iter`构造Python迭代器，并使用`next`从迭代器中获取第一项。 
1
next(iter(data_iter))# iter构造Python迭代器，并使用next从迭代器中获取第一项。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[tensor([[-0.4879,  0.5828],
		 [-0.2912, -0.0160],
		 [-2.0002,  2.0359],
		 [-0.3812,  1.3547],
		 [ 2.4167, -0.4777],
		 [ 0.3231, -1.6874],
		 [ 1.1544,  2.3415],
		 [ 0.1994, -0.4488],
		 [ 0.4064, -0.7453],
		 [ 0.6125,  0.6447]]),
 tensor([[ 1.2289],
		 [ 3.6639],
		 [-6.7296],
		 [-1.1639],
		 [10.6570],
		 [10.5763],
		 [-1.4631],
		 [ 6.1100],
		 [ 7.5428],
		 [ 3.2241]])]
### 1.4.3 定义模型 在上一节 [[dl-notes-1#2.1.3 线性回归的从零开始实现|从零实现线性回归]] 中实现线性回归时，我们明确定义了模型参数变量，并编写了计算的代码，这样通过基本的线性代数运算得到输出。 但对于标准深度学习模型，我们可以[**使用框架的预定义好的层**]。这使我们只需关注使用哪些层来构造模型，而不必关注层的实现细节。 首先定义一个模型变量`net`，它是一个`Sequential`类的实例。 - **Note**：`Sequential`类将多个层串联在一起。当给定输入数据时，`Sequential`实例将数据传入到第一层，然后将第一层的输出作为第二层的输入，以此类推。 回顾单层网络架构，这一单层被称为*全连接层*（fully-connected layer），因为它的每一个输入都通过矩阵-向量乘法得到它的每个输出。 在PyTorch中，全连接层在`Linear`类中定义。 值得注意的是，我们将两个参数传递到`nn.Linear`中。第一个指定输入特征形状，即 $2$，第二个指定输出特征形状，输出特征形状为单个标量，因此为 $1$。 
1
2
3
4
5
# nn是神经网络的缩写
from torch import nn

# Sequential一个容器，list of layers
net = nn.Sequential(nn.Linear(2, 1)) #nn.Linear为线性层函数，输入的纬度2；输出的纬度1，
### 1.4.4 初始化模型参数 在使用 `net` 之前，我们需要初始化模型参数——权重和偏置。 深度学习框架通常有预定义的方法来初始化参数。在这里，我们指定： - 权重参数：服从均值为 $0$、标准差为 $0.01$ 的正态分布 - 偏置参数：初始化为零。 正如在构造 `nn.Linear` 时指定输入和输出尺寸一样，现在我们能直接访问参数以设定它们的初始值。我们通过 `net[0]` 选择网络中的第一个图层，然后使用`weight.data` 和 `bias.data` 方法访问参数。我们还可以使用替换方法 `normal_` 和 `fill_` 来重写参数值。 
1
2
3
4
>>> net[0].weight.data.normal_(0, 0.01) #权重初始化，用normal方式
>>> net[0].bias.data.fill_(0) #初始化偏差为0

tensor([0.])
### 1.4.5 定义损失函数 [**计算均方误差使用的是`MSELoss`类，也称为平方$L_2$范数**]。 默认情况下，它返回所有样本损失的平均值。 
1
loss = nn.MSELoss() #均方误差函数
### 1.4.6 定义优化算法 小批量随机梯度下降算法是一种优化神经网络的标准工具，PyTorch 在`optim`模块中实现了该算法的许多变种。 当实例化一个`SGD`实例时，需要指定优化的参数（可通过`net.parameters()`从模型中获得）以及优化算法所需的超参数字典。小批量随机梯度下降只需要设置`lr`值，这里设置为 `0.03`。 
1
trainer = torch.optim.SGD(net.parameters(), lr=0.03) #随机梯度下降优化算法SGD，传入模型的参数，学习率lr
### 1.4.7 训练 通过深度学习框架的高级API来实现我们的模型只需要相对较少的代码。不必单独分配参数、不必定义我们的损失函数，也不必手动实现小批量随机梯度下降。 当我们需要更复杂的模型时，高级API的优势将大大增加。当我们有了所有的基本组件，**训练过程代码与从零开始实现时所做的非常相似**。 回顾一下：在每个迭代周期里，我们将完整遍历一次数据集（`train_data`），不停地从中获取一个小批量的输入和相应的标签。对于每一个小批量，我们会进行以下步骤: * 通过调用`net(X)`生成预测并计算损失`l`（前向传播）。 * 通过进行反向传播来计算梯度。 * 通过调用优化器来更新模型参数。 为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。 
1
2
3
4
5
6
7
8
9
num_epochs = 3 #迭代周期为3
for epoch in range(num_epochs):
    for X, y in data_iter:  #返回batch_size大小的数据
        l = loss(net(X) ,y) #计算损失函数
        trainer.zero_grad() #梯度清零
        l.backward() #计算梯度
        trainer.step() #更新参数
    l = loss(net(features), labels) #计算所有样本的loss
    print(f'epoch {epoch + 1}, loss {l:f}')
Results: 
1
2
3
epoch 1, loss 0.000239
epoch 2, loss 0.000095
epoch 3, loss 0.000096
下面我们 **比较生成数据集的真实参数和通过有限数据训练获得的模型参数**。要访问参数，我们首先从`net`访问所需的层，然后读取该层的权重和偏置。 正如在从零开始实现中一样，我们估计得到的参数与生成数据的真实参数非常接近。 
1
2
3
4
w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)
Results: 
1
2
w的估计误差： tensor([0.0002, 0.0007])
b的估计误差： tensor([-7.1526e-06])
## 1.5 小结 * 我们可以使用 `PyTorch` 的高级 `API` 更简洁地实现模型。 * 在 `PyTorch` 中，`data`模块提供了数据处理工具，`nn`模块定义了大量的神经网络层和常见损失函数。 * 可以通过`_`结尾的方法将参数替换，从而初始化参数。 ## 1.6 Q&A [00:00 Q&A](https://www.bilibili.com/video/BV1PX4y1g7KC?p=5&vd_source=ed04dacb9e3f8845a9f0fa7b8130e4f1&t=0) 1. **为什么使用平方损失而不是绝对差值？** > 其实差别不大，最开始使用平方损失是因为它可导，现在其实都可以使用。 2. **损失为什么要求平均？** > 本质上没有关系，但是如果不求平均，梯度的数值会比较大，这时需要学习率除以 $n$。如果不除以 $n$，可能会随着样本数量的增大而让梯度变得很大。 3. **不管是梯度下降还是随机梯度下降，怎么找到合适的学习率？** > - 选择对学习率不敏感的优化方法，比如 `Adam` > - 合理参数初始化 4. **训练过程中，过拟合和欠拟合情况下，学习率和`batch_size` 应该如何调整？** > 理论上学习率和 `batch_size` 对最后的拟合结果不会有影响。`batch_size` 越小，最终更容易收敛（一定的噪音对深度学习的泛化性有益） 5. **深度学习上，设置损失函数的时候，需要考虑正则吗？** >会考虑，但是和损失函数是分开的，深度学习中正则没有太大的用处，有很多其他的技术可以有正则的效果。 6. **如果样本大小不是批量数的整数倍，需要随机剔除多余的样本吗？** > 就取多余的样本作为一个批次 > 直接丢弃 > 从下一个 `epoch` 里面补少的样本 # 2 Softmax 回归 ## 2.1 Softmax 回归含义 [00:01 Softmax 回归](https://www.bilibili.com/video/BV1K64y1Q7wu?p=1&vd_source=ed04dacb9e3f8845a9f0fa7b8130e4f1&t=1.723515) ### 2.1.1 回归VS分类： - 回归估计一个连续值 - 分类预测一个离散类别 **典型的分类问题** 1. 蛋白质分类 [Link](https://www.kaggle.com/c/human-protein-atlas-image-classification) ![](https://cdn.jsdelivr.net/gh/YangSuoly/Images/dl-notes/202303192247370.png) 2. 恶意软件分类 [Link](https://www.kaggle.com/c/malware-classification) ![](https://cdn.jsdelivr.net/gh/YangSuoly/Images/dl-notes/202303192249308.png) 3. Wikipedia 评论分类 [Link](https://www.kaggle.com/c/jigsaw-toxic-comment-classification-challenge) ![](https://cdn.jsdelivr.net/gh/YangSuoly/Images/dl-notes/202303192250999.png) ### 2.1.2 从回归到多类分类 [02:37 从回归到分类](https://www.bilibili.com/video/BV1K64y1Q7wu?p=1&vd_source=ed04dacb9e3f8845a9f0fa7b8130e4f1&t=157.822685) <img src="https://cdn.jsdelivr.net/gh/YangSuoly/Images/dl-notes/202303192252047.png" style="zoom:67%;" /> 1. 回归： - 单连续数值输出 - 自然区间 $\mathbb{R}$ - 跟真实值的区别作为损失 2. 分类： - 通常多个输出 - 输出 $i$ 是预测为第 $i$ 类的置信度 **从回归到多类分类——均方损失** - 对类别进行一位有效编码 

\begin{array}{l}
\mathbf{y}=\left[y_1, y_2, \ldots, y_n\right]^{\top} \\
y_i=\left\{\begin{array}{l}
1 \text { if } i=y \\
0 \text { otherwise }
\end{array}\right.
\end{array}
$$

  • 使用均方损失训练

  • 最大值为预测

  • 输出匹配概率（非负，和为1）

    \hat{\mathbf{y}} & =\operatorname{softmax}(\mathbf{0}) \
    \hat{y}_i & =\frac{\exp \left(o_i\right)}{\sum_k \exp \left(o_k\right)}
    \end{aligned}

2.1.3 Softmax和交叉熵损失

  • 交叉熵用来衡量两个概率的区别

  • Softmax回归是一个多类分类模型

  • 使用Softmax操作子得到每个类的预测置信度

  • 使用交叉熵来衡量和预测标号的区别

2.2损失函数

00:16常用的损失函数

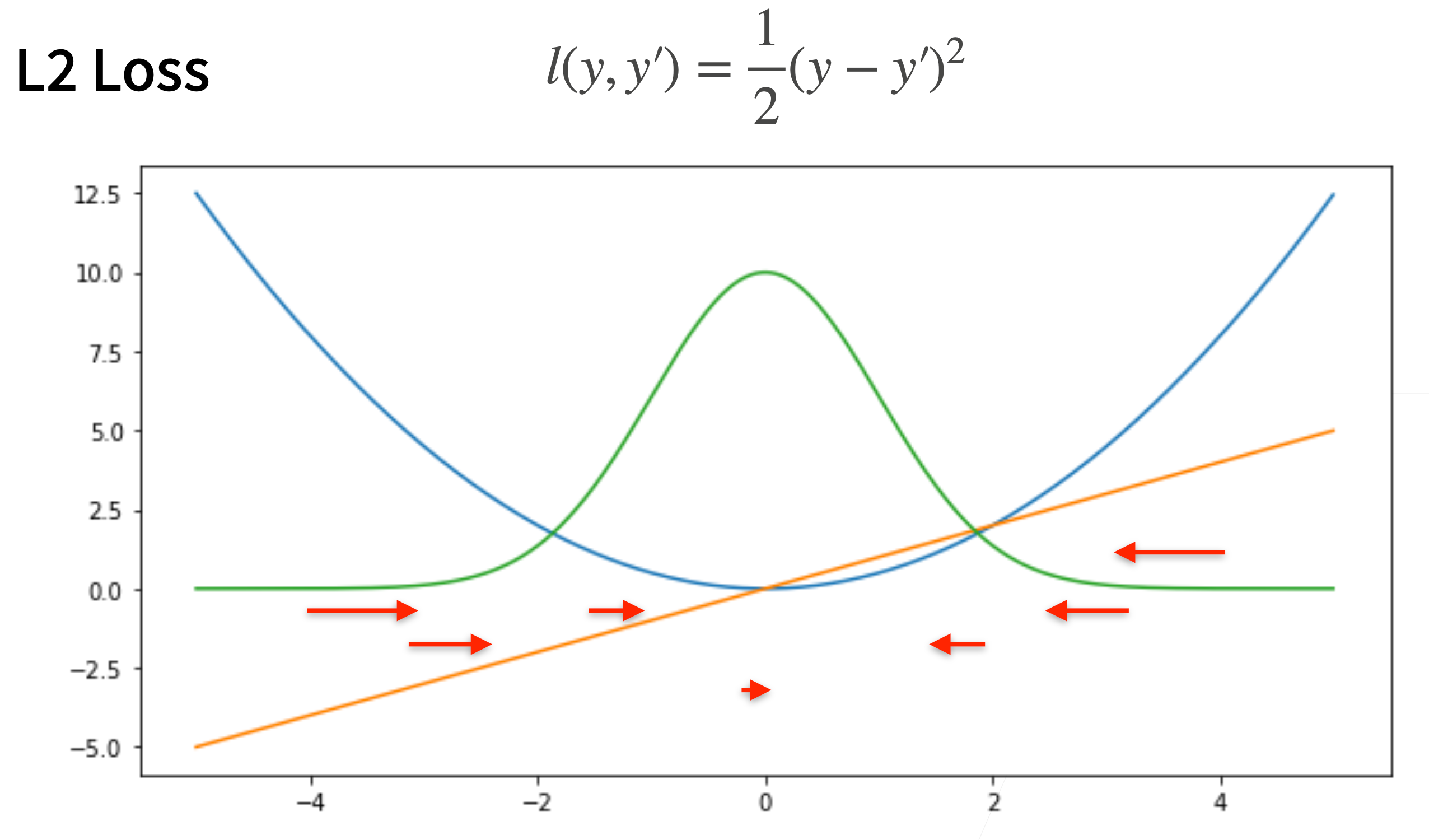
  1. 均方损失 L2 Loss

l(y,y′)=12(y−y′)2l\left(y, y^{\prime}\right)=\frac{1}{2}\left(y-y^{\prime}\right)^2

> 梯度会随着结果逼近而下降 2. L1 Loss

l(y,y′)=∣y−y′∣l\left(y, y^{\prime}\right)=\left|y-y^{\prime}\right|

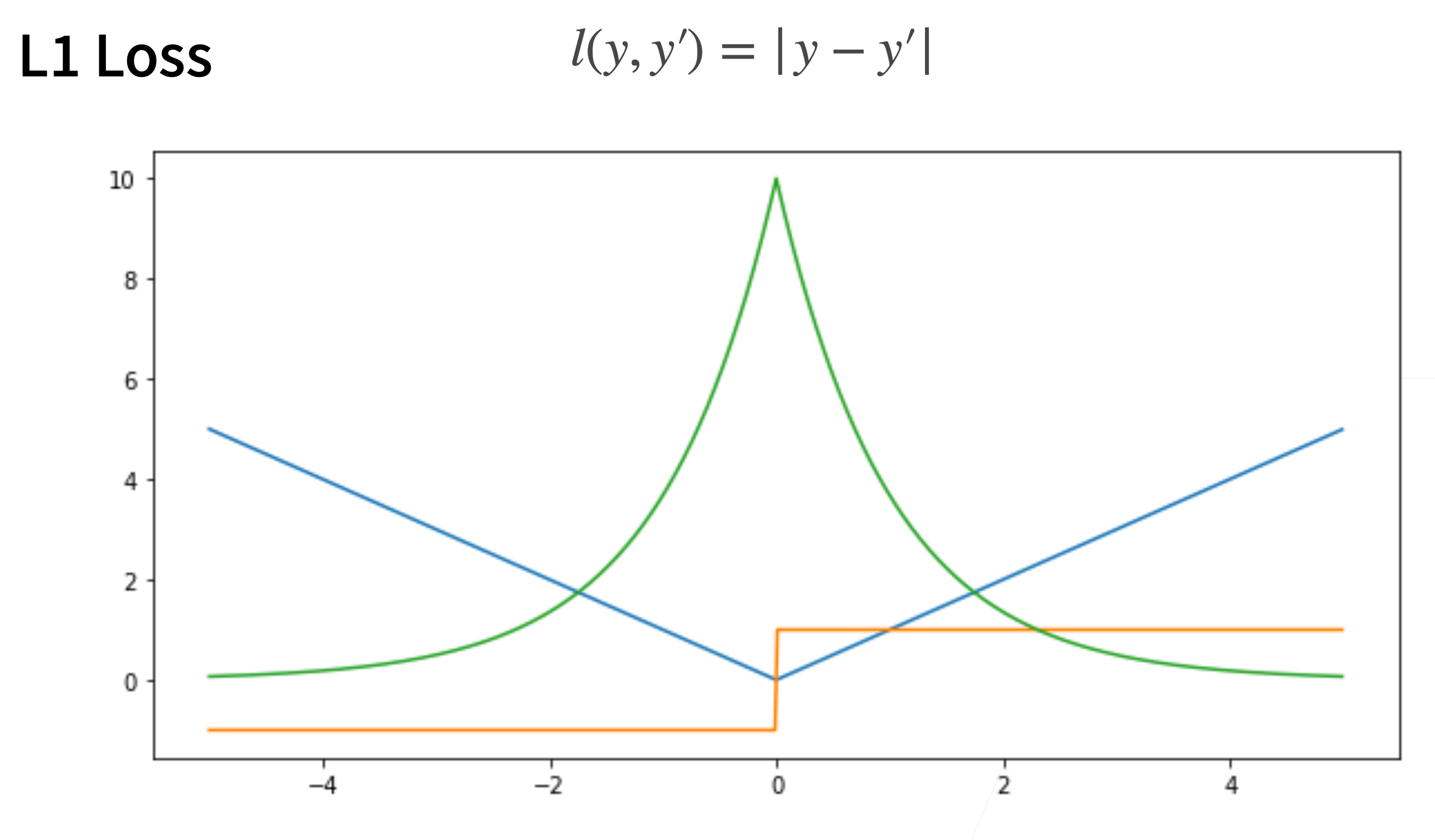> 梯度保持不变，但在0处梯度随机 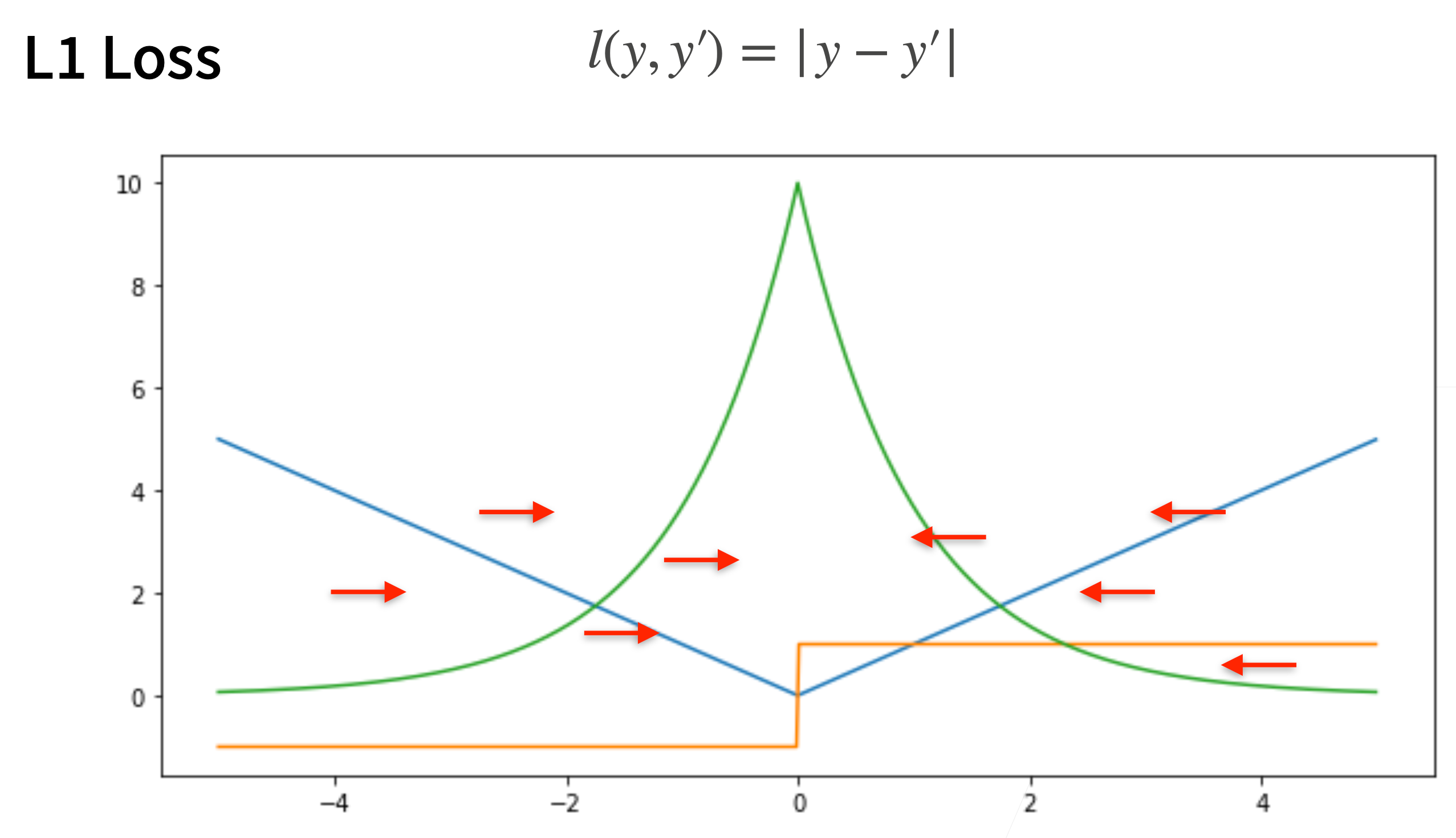3. Huber's Robust Loss

l(y,y′)={∣y−y′∣−12 if ∣y−y′∣>112(y−y′)2 otherwise l\left(y, y^{\prime}\right)=\left\{\begin{array}{ll} \left|y-y^{\prime}\right|-\frac{1}{2} & \text { if }\left|y-y^{\prime}\right|>1 \\ \frac{1}{2}\left(y-y^{\prime}\right)^2 & \text { otherwise } \end{array}\right.

结合L1 Loss和L2 Loss的优点

2.3 图片分类数据集

00:00 图片分类数据集

MNIST 数据集 (LeCun et al., 1998) 是图像分类中广泛使用的数据集之一，但作为基准数据集过于简单。我们将使用类似但更复杂的 Fashion-MNIST 数据集 (Xiao et al., 2017)：

2.3.1 读取数据集

  • 导入数据包

    1
    2
    3
    4
    5
    6
    7
    8
    %matplotlib inline
    import torch
    import torchvision
    from torch.utils import data
    from torchvision import transforms
    from d2l import torch as d2l

    d2l.use_svg_display()

可以通过框架中的内置函数将 Fashion-MNIST 数据集下载并读取到内存中*。

1
2
3
4
5
6
7
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0～1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root="../data", train=True, transform=trans, download=False)
mnist_test = torchvision.datasets.FashionMNIST(
    root="../data", train=False, transform=trans, download=False)
  • Note：因笔者提前下载了该数据集，因此此处将 dawnload 参数设置为 False，如果未下载，可以设置为 True。

Fashion-MNIST 由 1010 个类别的图像组成，
每个类别包含：

  • 训练数据集（train dataset）：6000张图像
  • 测试数据集（test dataset）：1000张图像

因此，训练集和测试集分别包含60000和10000张图像。测试数据集不会用于训练，只用于评估模型性能。

1
2
3
>>> len(mnist_train), len(mnist_test)

(60000, 10000)

每个输入图像的高度和宽度均为 2828 像素。
数据集由灰度图像组成，其通道数为 11。
为了简洁起见，本书将高度 hh 像素、宽度 ww 像素图像的形状记为 h×wh \times w 或（hh,ww）。

1
2
3
>>> mnist_train[0][0].shape

torch.Size([1, 28, 28])

2.3.2 可视化数据集的

Fashion-MNIST 中包含的10个类别，分别为:

  • t-shirt（T恤）
  • trouser（裤子）
  • pullover（套衫）
  • dress（连衣裙）
  • coat（外套）
  • sandal（凉鞋）
  • shirt（衬衫）
  • sneaker（运动鞋）
  • bag（包）
  • ankle boot（短靴）

以下函数用于在数字标签索引及其文本名称之间进行转换：

1
2
3
4
5
def get_fashion_mnist_labels(labels):  #@save
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

我们现在可以创建一个函数来可视化这些样本。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表"""
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    return axes

以下是训练数据集中前几个样本的图像及其相应的标签。

1
2
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y));
### 2.3.3 读取小批量

为了使我们在读取训练集和测试集时更容易，我们使用内置的数据迭代器，而不是从零开始创建。
回顾一下，在每次迭代中，数据加载器每次都会[读取一小批量数据，大小为batch_size]。
通过内置数据迭代器，我们可以随机打乱了所有样本，从而无偏见地读取小批量。

1
2
3
4
5
6
7
8
batch_size = 256

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
                             num_workers=get_dataloader_workers())

我们看一下读取训练数据所需的时间。

1
2
3
4
timer = d2l.Timer()
for X, y in train_iter:
    continue
f'{timer.stop():.2f} sec'

Results：

1
2.03 sec'

2.3.4 整合所有组件

现在我们定义 load_data_fashion_mnist 函数，用于获取和读取 Fashion-MNIST 数据集。

这个函数返回训练集和验证集的数据迭代器。
此外，这个函数还接受一个可选参数 resize，用来将图像大小调整为另一种形状。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=False)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=False)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

下面，我们通过指定resize参数来测试load_data_fashion_mnist函数的图像大小调整功能。

1
2
3
4
train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
    print(X.shape, X.dtype, y.shape, y.dtype)
    break

Results:

1
torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64

我们现在已经准备好使用Fashion-MNIST数据集，便于下面的章节调用来评估各种分类算法。

2.3.5 小结

  • Fashion-MNIST是一个服装分类数据集，由1010 个类别的图像组成。我们将在后续章节中使用此数据集来评估各种分类算法。
  • 我们将高度hh像素，宽度ww像素图像的形状记为h×wh \times w或（hh,ww）。
  • 数据迭代器是获得更高性能的关键组件。依靠实现良好的数据迭代器，利用高性能计算来避免减慢训练过程。

2.4 从零实现 Softmax回归

00:35 从零开始实现 Softmax

本节我们将使用上节的 Fashion-MNIST 数据集，
并设置数据迭代器的批量大小为256256，来实现softmax 回归的。

1
2
3
4
5
6
import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2.4.1 初始化模型参数

和之前线性回归的例子一样，这里的每个样本都将用固定长度的向量表示。

原始数据集中的每个样本都是 28×2828 \times 28 的图像。此处简单展平每个图像，把它们看作长度为784的向量。在后面的章节中，我们将讨论能够利用图像空间结构的特征，但此处暂时只把每个像素位置看作一个特征。

回想一下，在 softmax 回归中，我们的输出与类别一样多。(因为我们的数据集有10个类别，所以网络输出维度为10)。因此，权重将构成一个 784×10784 \times 10 的矩阵，偏置将构成一个1×101 \times 10的行向量。与线性回归一样，我们将使用正态分布初始化我们的权重 WW，偏置初始化为 00。

1
2
3
4
5
num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

2.4.2 定义 softmax 操作

1
2
X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)

Results：

1
2
3
(tensor([[5., 7., 9.]]),
 tensor([[ 6.],
		 [15.]]))
  • Note： 当调用sum运算符时，我们可以指定保持在原始张量的轴数，而不折叠求和的维度。
    这将产生一个具有形状(1, 3)的二维张量。

回想一下，[实现softmax]由三个步骤组成：

  1. 对每个项求幂（使用exp）；
  2. 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
  3. 将每一行除以其规范化常数，确保结果的和为1。

softmax的表达式：

softmax(X)ij=exp⁡(Xij)∑kexp⁡(Xik).\mathrm{softmax}(\mathbf{X})_{ij} = \frac{\exp(\mathbf{X}_{ij})}{\sum_k \exp(\mathbf{X}_{ik})}.

分母或规范化常数，有时也称为配分函数（其对数称为对数-配分函数）。该名称来自统计物理学 中一个模拟粒子群分布的方程。

1
2
3
4
def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

正如上述代码，对于任何随机输入，我们将每个元素变成一个非负数。此外，依据概率原理，每行总和为 11。

1
2
3
X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)

Results:

1
2
3
4
(tensor([[0.2135, 0.5900, 0.0449, 0.1064, 0.0453],
		 [0.3128, 0.1832, 0.1076, 0.3053, 0.0910]]),

 tensor([1.0000, 1.0000]))

Note：虽然这在数学上看起来是正确的，但我们在代码实现中有点草率。矩阵中的非常大或非常小的元素可能造成数值上溢或下溢，但我们没有采取措施来防止这点。

2.4.3 定义模型

05:37 定义模型

定义操作后，我们可以实现 softmax 回归模型。下面的代码定义了输入如何通过网络映射到输出。

Note：将数据传递到模型之前，我们使用reshape函数将每张原始图像展平为向量。

1
2
def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

2.4.4 定义损失函数

06:49 损失函数

接下来，我们实现交叉熵损失函数。这可能是深度学习中最常见的损失函数，因为目前分类问题的数量远远超过回归问题的数量。

回顾一下，交叉熵采用真实标签的预测概率的负对数似然。

Note：这里不使用 for 循环迭代预测（这往往是低效的），而是通过一个运算符选择所有元素。

下面，我们创建一个数据样本 y_hat ，其中包含2个样本在3个类别的预测概率，以及它们对应的标签y。
有了 y。

我们知道在第一个样本中，第一类是正确的预测；而在第二个样本中，第三类是正确的预测。然后使用y作为 y_hat 中概率的索引，我们选择第一个样本中第一个类的概率和第二个样本中第三个类的概率。

1
2
3
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]

Results:

1
tensor([0.1000, 0.5000])

现在我们只需一行代码就可以实现交叉熵损失函数。

1
2
3
4
def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

cross_entropy(y_hat, y)

Results:

1
tensor([2.3026, 0.6931])

2.4.5 分类精度

09:40 分类精度

给定预测概率分布 y_hat ，当我们必须输出硬预测（hard prediction）时，我们通常选择预测概率最高的类。

当预测与标签分类 y 一致时，即是正确的。
分类精度 即正确预测数量与总预测数量之比。
虽然直接优化精度可能很困难（因为精度的计算不可导），但精度通常是我们最关心的性能衡量标准，我们在训练分类器时几乎总会关注它。

为了计算精度，我们执行以下操作。

  1. 如果 y_hat 是矩阵，那么假定第二个维度存储每个类的预测分数。使用 argmax 获得每行中最大元素的索引来获得预测类别。

  2. 将预测类别与真实 y 元素进行比较。

    由于等式运算符 == 对数据类型很敏感，因此我们将y_hat的数据类型转换为与y的数据类型一致。结果是一个包含0（错）和1（对）的张量。

  3. 最后，我们求和会得到正确预测的数量。

1
2
3
4
5
6
def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

我们将继续使用之前定义的变量 y_hat 和 y 分别作为预测的概率分布和标签。

可以看到，第一个样本的预测类别是 22（该行的最大元素为 0.60.6，索引为 22），这与实际标签 00 不一致。
第二个样本的预测类别是 22（该行的最大元素为 0.50.5，索引为 22），这与实际标签 22 一致。
因此，这两个样本的分类精度率为 0.50.5。

1
accuracy(y_hat, y) / len(y)

Results:

1
0.5

同样，对于任意数据迭代器 data_iter 可访问的数据集，我们可以评估在任意模型 net 的精度。

1
2
3
4
5
6
7
8
9
def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

这里定义一个实用程序类 Accumulator，用于对多个变量进行累加。在上面的evaluate_accuracy函数中，我们在 Accumulator 实例中创建了2个变量，
分别用于存储正确预测的数量和预测的总数量。
当我们遍历数据集时，两者都将随着时间的推移而累加。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

由于我们使用随机权重初始化net模型，
因此该模型的精度应接近于随机猜测。
例如在有10个类别情况下的精度为0.1。

1
evaluate_accuracy(net, test_iter)

Results:

1
0.0508

2.4.6 训练

12:29 训练

在我们看过 [[dl-notes-2#2.1.3 线性回归的从零开始实现|从零开始实现线性回归]] 中的线性回归实现， softmax 回归的训练过程代码应该看起来非常眼熟。在这里，我们重构训练过程的实现以使其可重复使用。

首先，定义一个函数来训练一个迭代周期。请注意， updater 是更新模型参数的常用函数，它接受批量大小作为参数。它可以是 d2l.sgd 函数，也可以是框架的内置优化函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

在展示训练函数的实现之前，我们[定义一个在动画中绘制数据的实用程序类]Animator，它能够简化本书其余部分的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(4.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

接下来我们实现一个训练函数，它会在 train_iter 访问到的训练数据集上训练一个模型 net。该训练函数将会运行多个迭代周期（由 num_epochs 指定）。

在每个迭代周期结束时，利用 test_iter 访问到的测试数据集对模型进行评估。我们将利用 Animator 类来可视化训练进度。

1
2
3
4
5
6
7
8
9
10
11
12
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

作为一个从零开始的实现，我们使用小批量随机梯度下降来优化模型的损失函数，设置学习率为 0.10.1。

1
2
3
4
lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

现在，我们训练模型10个迭代周期。

  • Note：迭代周期（num_epochs）和学习率（lr）都是可调节的超参数。通过更改它们的值，我们可以提高模型的分类精度。
1
2
num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

Results：

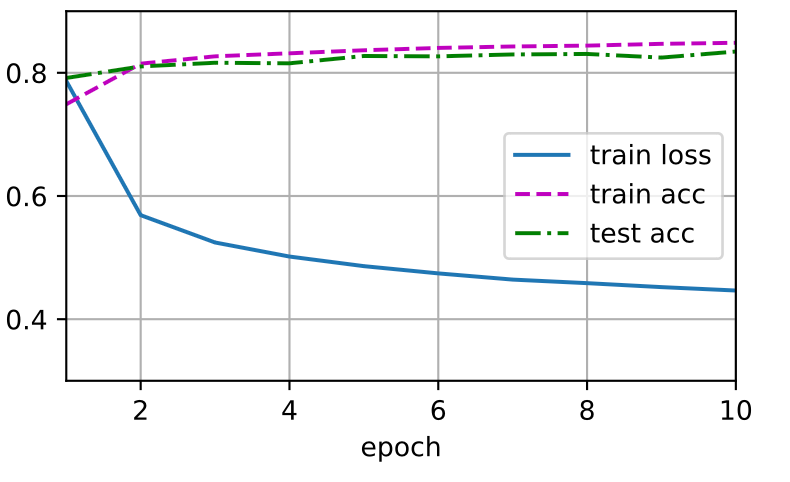### 2.4.7 预测

现在训练已经完成，我们的模型已经准备好对图像进行分类预测。给定一系列图像，我们将比较它们的实际标签（文本输出的第一行）和模型预测（文本输出的第二行）。

1
2
3
4
5
6
7
8
9
10
11
def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)
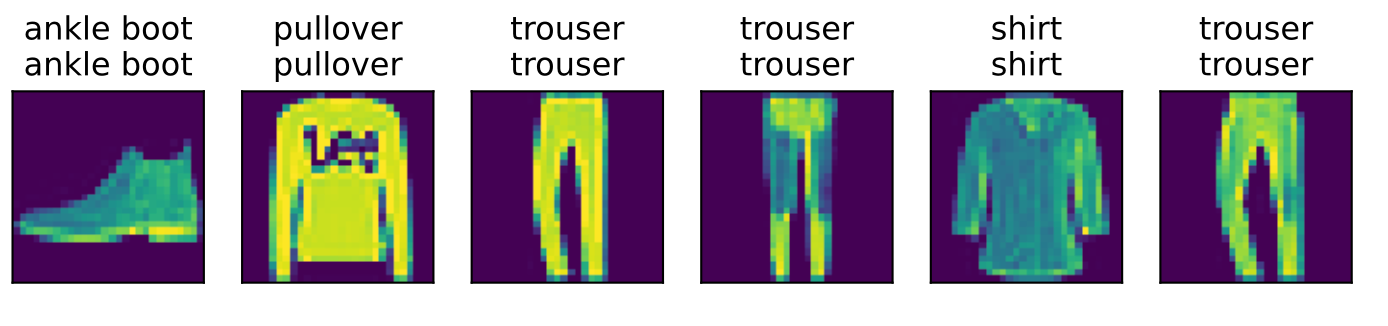### 2.4.8 小结
  • 借助 softmax 回归，我们可以训练多分类的模型。
  • 训练 softmax 回归循环模型与训练线性回归模型非常相似：先读取数据，再定义模型和损失函数，然后使用优化算法训练模 python 型。大多数常见的深度学习模型都有类似的训练过程。

2.5 Softmax 简洁实现

00:00 Softmax 简洁实现

在 [[dl-notes-2#2.1.4 调用 API 实现|简洁实现线性回归]] 中，我们发现通过深度学习框架的高级API能够使实现线性回归变得更加容易。同样，通过深度学习框架的高级 API 也能更方便地实现 softmax 回归模型。

本节同上一节一样，继续使用 Fashion-MNIST 数据集，并保持批量大小为 256 。

1
2
3
4
5
6
import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2.5.1 初始化模型参数

如我们在 [[dl-notes-2#2.2 Softmax 回归|Softmax 回归]] 所述， softmax 回归的输出层是一个全连接层。
因此，为了实现模型，只需在 Sequential 中添加一个带有 1010 个输出的全连接层。

  • Note：同样，在这里 Sequential 并不是必要的，但它是实现深度模型的基础。仍然以均值 00 和标准差 0.010.01 随机初始化权重。
1
2
3
4
5
6
7
8
9
# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

Note： PyTorch 不会隐式地调整输入的形状。因此，我们在线性层前定义了展平层（flatten），来调整网络输入的形状。

2.5.2 重新审视Softmax的实现

在前面 [[dl-notes-2#2.2.4 从零实现 Softmax回归|从零实现 Softmax回归]] 的例子中，我们计算了模型的输出，然后将此输出送入交叉熵损失。从数学上讲，这是一件完全合理的事情。然而，从计算角度来看，指数可能会造成数值稳定性问题。

回想一下， softmax 函数：

y^j=exp⁡(oj)∑kexp⁡(ok)\hat y_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}

其中， y^j\hat y_j 是预测的概率分布，ojo_j 是未规范化的预测 o\mathbf{o} 的第 jj 个元素。

如果 oko_k 中的一些数值非常大，那么 exp⁡(ok)\exp(o_k) 可能大于数据类型容许的最大数字，即上溢（overflow）。
这将使分母或分子变为 inf （无穷大），
最后得到的是0、inf 或 nan（不是数字）的 y^j\hat y_j。在这些情况下，我们无法得到一个明确定义的交叉熵值。

解决技巧：

  • 在继续softmax计算之前，先从所有oko_k中减去 max⁡(ok)\max(o_k) 。这里可以看到每个oko_k按常数进行的移动不会改变 softmax 的返回值：

    \hat y_j & = \frac{\exp(o_j - \max(o_k))\exp(\max(o_k))}{\sum_k \exp(o_k - \max(o_k))\exp(\max(o_k))} \
    & = \frac{\exp(o_j - \max(o_k))}{\sum_k \exp(o_k - \max(o_k))}.
    \end{aligned}

尽管我们要计算指数函数，但我们最终在计算交叉熵损失时会取它们的对数。通过将 softmax 和交叉熵结合在一起，可以避免反向传播过程中可能会困扰我们的数值稳定性问题。

如下面的等式所示，我们避免计算exp⁡(oj−max⁡(ok))\exp(o_j - \max(o_k))，而可以直接使用 oj−max⁡(ok)o_j - \max(o_k) ，因为 log⁡(exp⁡(⋅))\log(\exp(\cdot)) 被抵消了。

log⁡(y^j)=log⁡(exp⁡(oj−max⁡(ok))∑kexp⁡(ok−max⁡(ok)))=log⁡(exp⁡(oj−max⁡(ok)))−log⁡(∑kexp⁡(ok−max⁡(ok)))=oj−max⁡(ok)−log⁡(∑kexp⁡(ok−max⁡(ok))).\begin{aligned} \log{(\hat y_j)} & = \log\left( \frac{\exp(o_j - \max(o_k))}{\sum_k \exp(o_k - \max(o_k))}\right) \\ & = \log{(\exp(o_j - \max(o_k)))}-\log{\left( \sum_k \exp(o_k - \max(o_k)) \right)} \\ & = o_j - \max(o_k) -\log{\left( \sum_k \exp(o_k - \max(o_k)) \right)}. \end{aligned}

我们希望保留传统的 softmax 函数，以用于评估模型输出的概率。但是，我们并没有在交叉熵损失函数中传递 softmax 概率，而是传递了未规范化的预测，并同时计算了 softmax 及其对数。这种方法类似于"LogSumExp技巧"技巧。

2.5.3 损失函数

1
loss = nn.CrossEntropyLoss(reduction='none')

2.5.4 优化算法

在这里，我们使用学习率为 0.10.1 的小批量随机梯度下降作为优化算法。

1
trainer = torch.optim.SGD(net.parameters(), lr=0.1)

2.5.5 训练

接下来我们调用上一节中定义的训练函数来训练模型。

1
2
3
4
5
6
7
8
9
try:
    d2l.train_ch3()
except:
    print("module 'd2l.torch' has no attribute 'train_ch3'")

try:
    d2l.train_epoch_ch3train_epoch_ch3()
except:
    print("module 'd2l.torch' has no attribute 'train_epoch_ch3'")

Results:

1
2
3
module 'd2l.torch' has no attribute 'train_ch3'

module 'd2l.torch' has no attribute 'train_epoch_ch3'
- **Note**：可以发现，此处直接调用 `d2l.train_ch3` 会报错。这可能是由于笔者安装的 `d2l` 版本与李沐老师是视频中（[02:31 训练模型](https://www.bilibili.com/video/BV1K64y1Q7wu?p=5&vd_source=ed04dacb9e3f8845a9f0fa7b8130e4f1&t=151.585906)）展示的代码颇有不同，因此直接调用上一节的部分代码，并进行了改写。

  • train_epoch_ch3 函数

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    def train_epoch_ch3(net, train_iter, loss, updater):  #@save
        """训练模型一个迭代周期（定义见第3章）"""
        # 将模型设置为训练模式
        if isinstance(net, torch.nn.Module):
            net.train()
        # 训练损失总和、训练准确度总和、样本数
        metric = d2l.Accumulator(3)
        for X, y in train_iter:
            # 计算梯度并更新参数
            y_hat = net(X)
            l = loss(y_hat, y)
            if isinstance(updater, torch.optim.Optimizer):
                # 使用PyTorch内置的优化器和损失函数
                updater.zero_grad()
                l.mean().backward()
                updater.step()
            else:
                # 使用定制的优化器和损失函数
                l.sum().backward()
                updater(X.shape[0])
            metric.add(float(l.sum()), d2l.accuracy(y_hat, y), y.numel())
        # 返回训练损失和训练精度
        return metric[0] / metric[2], metric[1] / metric[2]

  • train

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    num_epochs = 10

    def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
        """训练模型（定义见第3章）"""
        animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                            legend=['train loss', 'train acc', 'test acc'], figsize=(4.5, 2.5))
        for epoch in range(num_epochs):
            train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
            test_acc = d2l.evaluate_accuracy_gpu(net, test_iter)
            animator.add(epoch + 1, train_metrics + (test_acc,))
        train_loss, train_acc = train_metrics
        assert train_loss < 0.5, train_loss
        assert train_acc <= 1 and train_acc > 0.7, train_acc
        assert test_acc <= 1 and test_acc > 0.7, test_acc
        
    train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
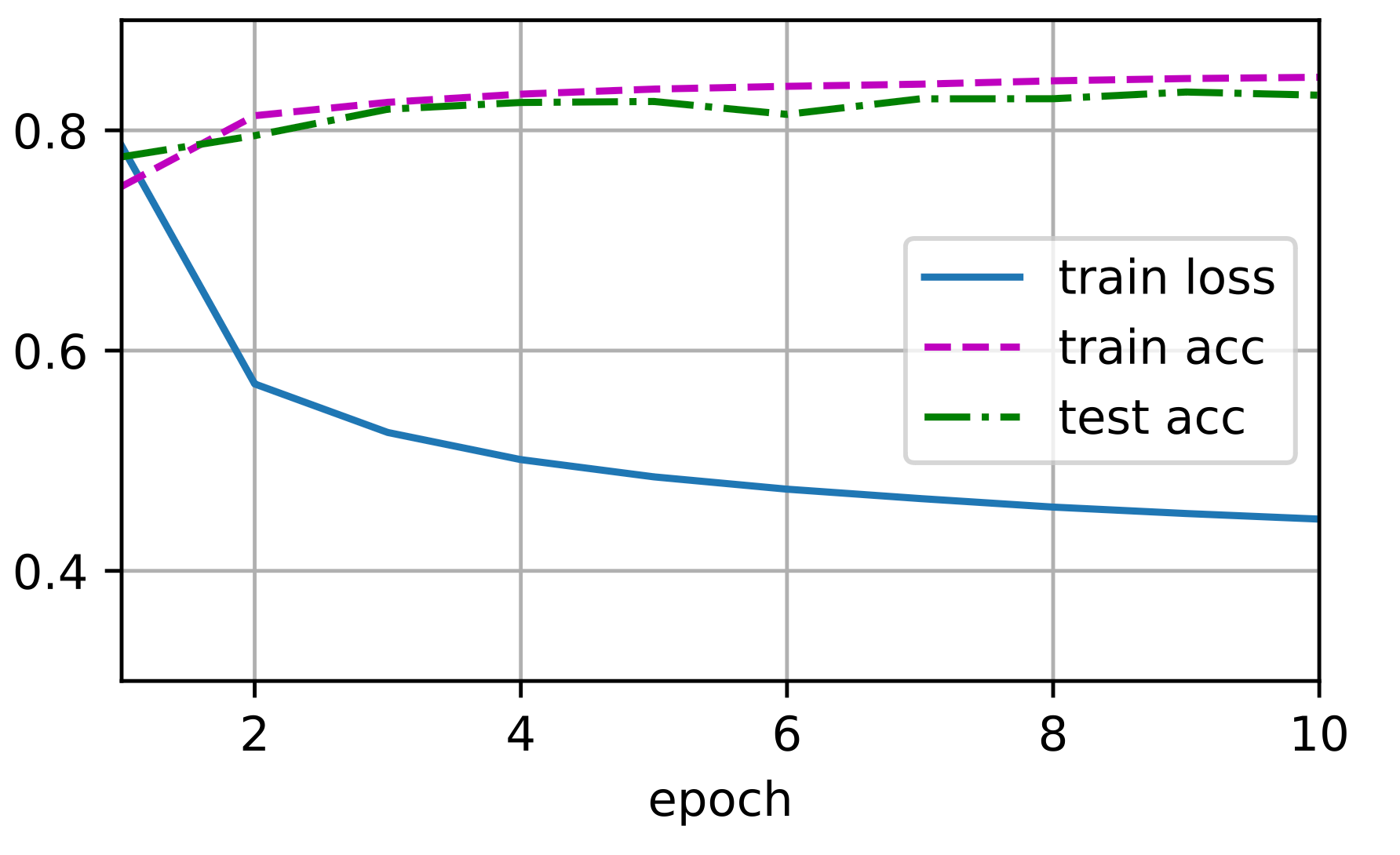和以前一样，这个算法使结果收敛到一个相当高的精度，而且这次的代码比之前更精简了。

2.5.6小结

  • 使用深度学习框架的高级API，我们可以更简洁地实现 softmax 回归。
  • 从计算的角度来看，实现 softmax 回归比较复杂。在许多情况下，深度学习框架在这些著名的技巧之外采取了额外的预防措施，来确保数值的稳定性。这使我们避免了在实践中从零开始编写模型时可能遇到的陷阱。

2.6 softmax回归Q&A

04:09 Q&A

  • Q1:softlabel训练策略以及为什么有效？

softmax用指数很难逼近1，softlabel将正例和负例分别标记为0.9和0.1使结果逼近变得可能，这是一个常用的小技巧。

  • Q2:softmax回归和logistic回归？

logistic回归为二分类问题，是softmax回归的特例

  • Q3:为什么使用交叉熵，而不用相对熵，互信息熵等其他基于信息量的度量？

实际上使用哪一种熵的效果区别不大，所以哪种简单就用哪种

  • Q4: y∗log⁡y^y * \log \hat{y} 为什么我们只关心正确类，而不关心不正确的类呢？

并不是不关心，而是不正确的的类标号为零，所以算式中不体现，如果使用softlabel策略，就会体现出不正确的类。

  • Q5:似然函数曲线是怎么得出来的？有什么参考意义？

最小化损失函数也意味着最大化似然函数，似然函数表示统计概率和模型的拟合程度。

  • Q6:在多次迭代之后欧如果测试精度出现上升后再下降是过拟合了吗？可以提前终止吗？

很有可能是过拟合，可以继续训练来观察是否持续下降

  • Q7:cnn网络主要学习到的是纹理还是轮廓还是所有内容的综合？

目前认为主要学习到的是纹理信息

  • Q8:softmax可解释吗？

单纯softmax是可解释的，可以在统计书籍中找到相关的解释。

-------------This blog is over! Thanks for your reading-------------