0. Preface

本系列博文是 DataWhale 社区 2023年 3月《动手学深度学习（Pytorch）》组队学习活动的笔记，本篇为系列笔记的第一篇—— 初识深度学习和预备知识整理。

本文是学习李沐老师 B 站视频教程动手学深度学习 PyTorch版所记录的笔记。主要使用 Obsidian 软件并借助插件 Meida extended 插件，在 markdown 文件中生成时间戳，可以在后期温习笔记时，方便地定位到原视频所在位置。

原教程视频如下：

PDF 版本笔记见：D2L Note Chapter 1

本次活动面向的人员：

有Python基础
有高数，线代，概率论基础
本科大二左右，或者研一

学习资源整合

教材：Link
纸质书：Link（最低折扣五折购买地址）
视频：Link
笔记：Link
竞赛：Link
OpenI云环境（可直接运行）：Link

1 课程安排

动手学深度学习课程安排

1.1 课程目标

介绍深度学习经典和最新模型
- LeNet, ResNet, LSTM, BERT, ...
机器学习基础
- 损失函数、目标函数、过拟合、优化
实践
- 使用Pytorch实现介绍的知识点
- 在真实数据上体验算法效果

1.2 内容

> 深度学习基础：线性神经网络，多层感知机 > > 卷积神经网络：LeNet, AlexNet, VGG, Inception, ResNet > > 循环神经网络：RNN，GRU，LSTM，seq2seq > > 注意力机制：Attention， Transformer > > 优化算法：SGD，Momentum，Adam > > 高性能计算：并行，多GPU，分布式 > > 计算机视觉：目标检测，语义分割 > > 自然语言处理：词嵌入，BERT

1.3 学到什么

04:48 可以学到什么

What：深度学习有哪些技术，以及哪些技术可以帮你解决问题
How：如何实现（产品 or paper）和调参（精度or速度）
Why：背后的原因（直觉、数学）

1.4 基本要求

AI相关从业人员（产品经理等）：掌握What，知道名词，能干什么
数据科学家、工程师：掌握What、How，手要快，能出活
研究员、学生：掌握What、How、Why，除了知道有什么和怎么做，还要知道为什么，思考背后的原因，做出新的突破

1.5 课程资源

07:33

课程主页：https://courses.d2l.ai/zh-v2/
教材：https://zh-v2.d2l.ai/
课程论坛讨论：https://discuss.d2l.ai/c/chinese-version/16
Pytorch论坛：https://discuss.pytorch.org/
b站视频合集：[https://space.bilibili.com/1567748478/channel/seriesdetail?sid=358497]

2 深度学习介绍

Introduction to DL Link

2.1 概述

0:1 什么是深度学习

0:13 AI 地图

首先画一个简单的人工智能地图：

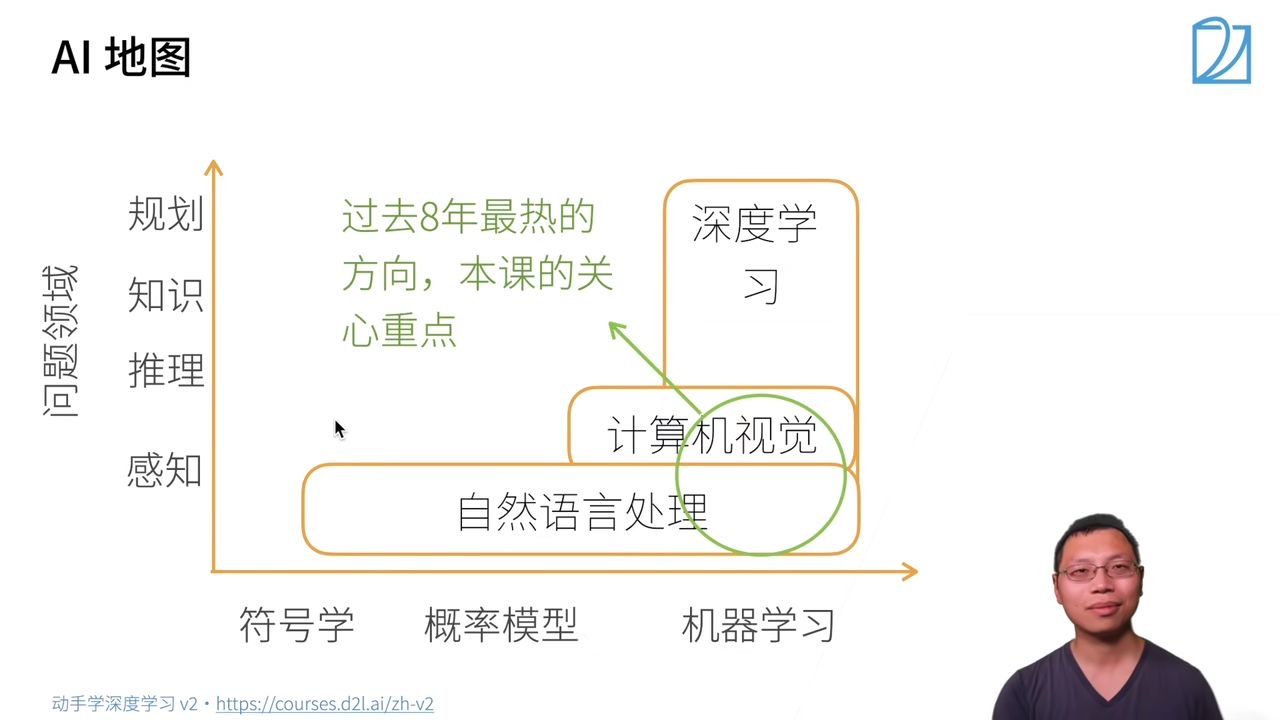
- x轴表示不同的模式or方法：最早的是符号学，接下来是概率模型，之后是机器学习

y轴表示可以达到的层次：由底部向上依次是

感知：了解是什么，比如能够可以看到物体，如面前的一块屏幕

推理：基于感知到的现象，想象或推测未来会发生什么

知识：根据看到的数据或者现象，形成自己的知识

规划：根据学习到的知识，做出长远的规划

AI地图解读

问题领域的一个简单分类
- 自然语言处理：
  - 停留在比较简单的感知层面，比如自然语言处理用的比较多的机器翻译，给一句中文翻译成英文，很多时候是人的潜意识里面大脑感知的一个问题。一般来说，人可以几秒钟内反应过来的东西，属于感知范围。
  - 自然语言处理最早使用的方法是符号学，由于语言具有符号性；之后一段时间比较流行的有概率模型，以及现在也用的比较多的机器学习。
- 计算机视觉：
  - 在简单的感知层次之上，可以对图片做一些推理。
  - 图片里都是一些像素，很难用符号学解释，所以一般采用概率模型和机器学习。
- 深度学习
  - 机器学习的一种，更深层的神经网络。
  - 可以做计算机视觉，自然语言处理，强化学习等。
过去八年最热的方向，也是本课程关心的重点：
- 深度学习+计算机视觉 / 自然语言处理

2.2 深度学习的应用

3:59 图片分类

深度学习最早是在图片分类上有比较大的突破，ImageNet 是一个比较大的图片分类数据集，

x轴：年份 y轴：错误率 圆点：表示某年份某研究工作/paper的错误率 IMAGENET 数据来源

在2010年时，错误率比较高，最好的工作错误率也在26%、27%左右；

在2012年，有团队首次使用深度学习将错误率降到25%以下；

在接下来几年中，使用深度学习可以将误差降到很低。

2017年基本所有的团队可以将错误率降到5%以下，基本可以达到人类识别图片的精度。

4:43 物体检测和分割

当你不仅仅想知道图片里有什么内容，还想知道物体是什么，在什么位置，这就是物体检测。物体分割是指每一个像素属于什么，属于飞机还是属于人(如下图)，这是图像领域更深层次的一个应用。

5:15 样式迁移

原图片+想要迁移的风格=风格迁移后的图片，加了一个可以根据输入改变图片风格的滤镜。

6:1 人脸合成

下图中所有的人脸都是假的，由机器合成的图片：

6:25 文生图

1. 描述：一个胡萝卜宝宝遛狗的图片。 2. 描述：一个牛油果形状的靠背椅。

7:2 文字生成

> 示例1： > > 问题输入：如何举行一个有效的董事会议 > > 机器输出：生成篇章回答

示例2：

输入：将Students从School这个table中选出来

输出：用于查询的SQL语言

7:56 无人驾驶

识别车、道路以及各种障碍物等，并规划路线。

8:29 案例研究-广告点击

用户输入想要搜索的广告内容，如：baby toy

网站呈现最具有效益的广告(用户更可能点击，且给网站带来更高经济效益)

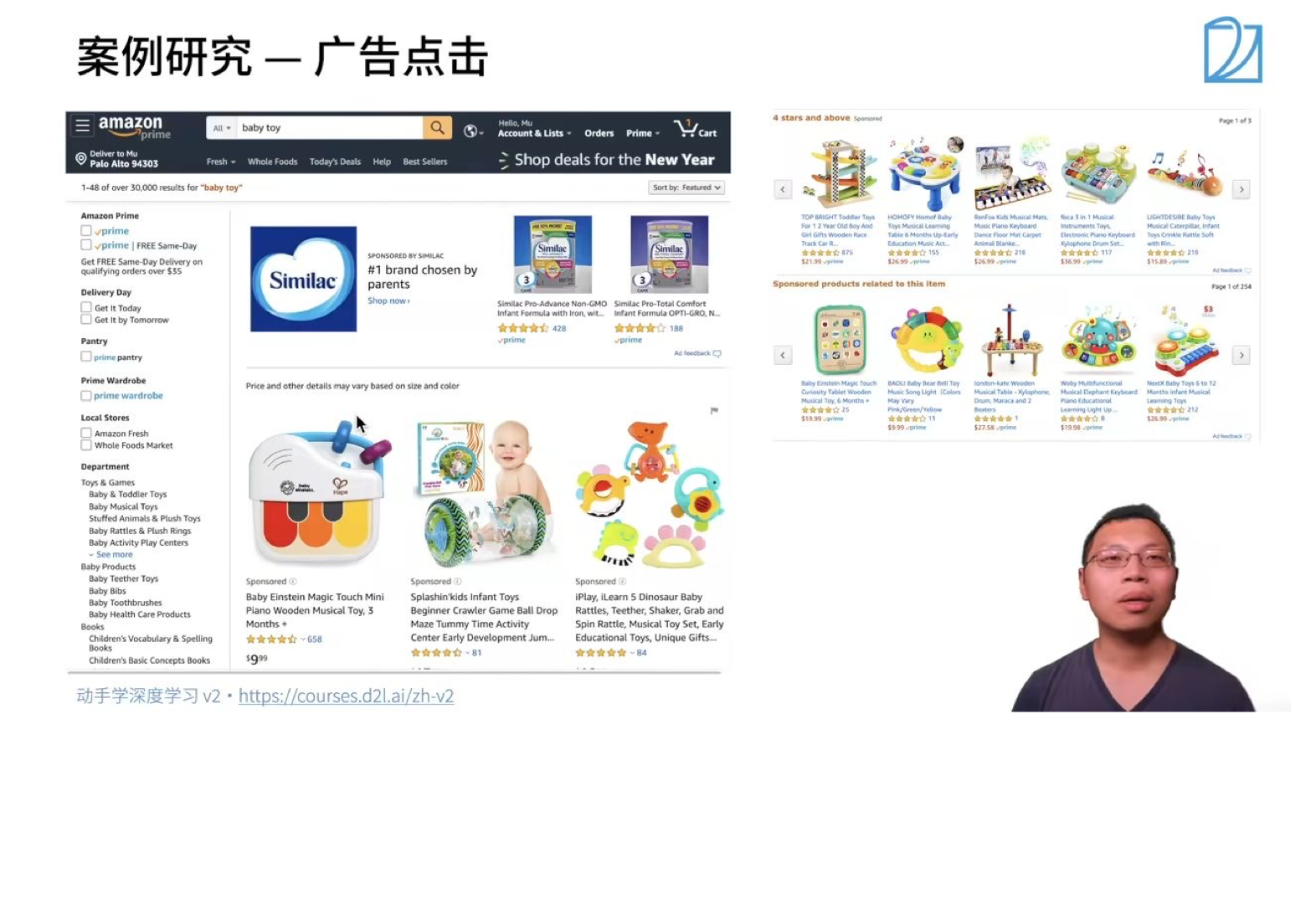
步骤： 1. 触发：用户输入关键词，机器先找到一些相关的广告 2. 点击率预估：利用机器学习的模型预测用户对广告的点击率 3. 排序：利用点击率x竞价的结果进行排序呈现广告，排名高的在前面呈现

模型的训练与预测：

上述步骤的第二步中涉及到模型预测用户的点击率，具体过程如下：

- 模型预测 数据 (待预测广告) → 特征提取 → 模型 → 点击率预测

模型训练 训练数据 (过去广告展现和用户点击) → 特征(X)和用户点击(Y) → 喂给模型训练

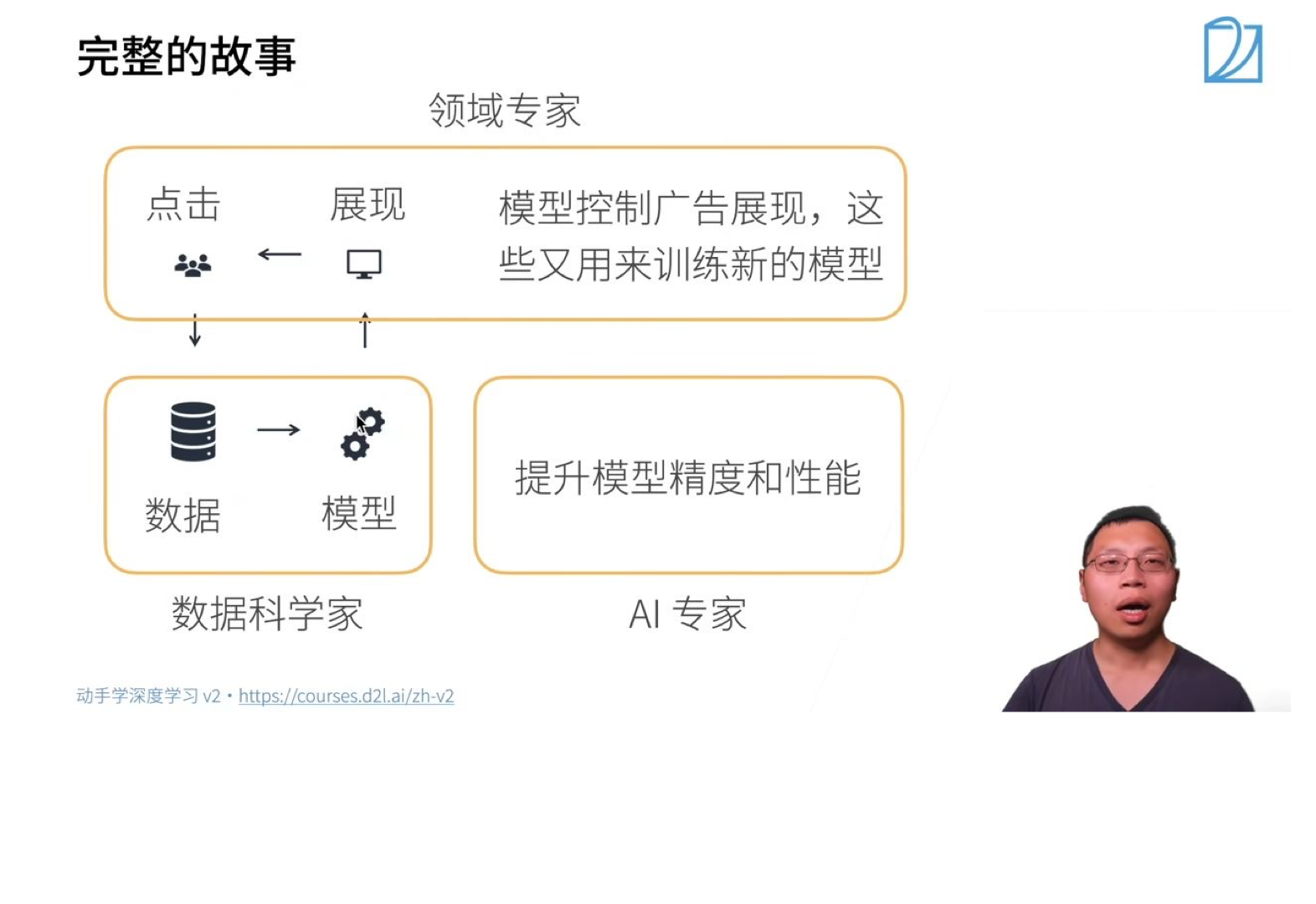
- 领域专家：对特定的应用有比较深的了解，根据展现情况以及用户点击分析用户的行为，期望模型对应用做一些拟合，符合真实数据和分析情况。 - 数据科学家：利用数据训练模型，训练后模型投入使用，进行预测呈现。 - AI专家：应用规模扩大，用户数量增多，模型更加复杂，需要进一步提升精度和性能。

2.3 总结

通过AI地图，课程从纵向和横向两个维度解读了深度学习在重要问题领域的概况。
介绍了深度学习在CV和NLP方面的一些应用
简单分析并研究了深度学习实例——广告点击。

3 安装

课程链接

3.1 安装python

02:04 安装python

首先前提是安装python，这里推荐安装python3.8 输入命令 sudo apt install python3.8 即可

3.2安装Miniconda/Anaconda

然后第二步，安装 Miniconda（如果已经安装conda或者Miniconda，则可以跳过该步骤)。 #### 2.1 安装Miniconda

安装MIniconda的好处是可以创建很多虚拟环境，并且不同环境之间互相不会有依赖关系，对日后的项目有帮助，如果只想在本地安装的话，不装Miniconda只使用pip即可，第二步可以跳过。

如果是Windows系统，输入命令

1	wget https://repo.anaconda.com/miniconda/Miniconda3-py38_4.10.3-Windows-x86_64.exe

如果是macOS，输入命令：

1	wget https://repo.anaconda.com/miniconda/Miniconda3-py38_4.10.3-Linux-x86_64.sh

之后要输入命令

1	sh Miniconda3-py38_4.10.3-MacOSX-x86_64.sh -b

如果是Linux系统，输入命令 ****** 之后输入命令
1
sh Miniconda3-py38_4.10.3-Linux-x86_64.sh -b
以上都是基于python3.8版本，对于其他版本，可以访问 https://docs.conda.io/en/latest/miniconda.html ，下载对应版本即可。

2.2 Miniconda环境配置

!pip install d2l
import numpy as np
import torch
from torch.utils import data 
from d2l import torch as d2l

Note：笔者是 Mac-M1 系统，需要注意的是，此处推荐使用 Python 3.9 环境，如果使用 3.10 版本可能会报如下错误：

ValueError Traceback (most recent call last)  
Input In [1], in <cell line: 4>()  
1 #import torch  
2 #print(torch.**version**)  
----> 4 from d2l import torch as d2l

... 

---> 13 from pandas._libs.interval import Interval  
14 from pandas._libs.tslibs import (  
15 NaT,  
16 NaTType,  
(...)  
21 iNaT,  
22 )

File pandas/_libs/interval.pyx:1, in init pandas._libs.interval()

ValueError: numpy.ndarray size changed, may indicate binary incompatibility. Expected 96 from C header, got 88 from PyObject

解决办法：重装pandas

1	pip install --force-reinstall pandas

只需要重新安装 miniconda 和 python 版本就好，步骤：

从官网下载 3.9 版本的 miniconda，然后运行：

1 2	# execute the following at the download location: sh Miniconda3-py39_23.1.0-1-MacOSX-arm64.sh -b

初始化 miniconda：

1 2	# initiate the shell conda activate ~/miniconda3

或者（二选一）：

1	~/miniconda3/bin/conda init

创建虚拟环境
1
conda create --name d2l python=3.9 -y
激活虚拟环境
1
conda actiavte d2l
下载 torch-gpu 版本（选）

考虑到后续可能需要 gpu 加速训练，因此此处直接下载 torch-gpu 版本。
1
pip install --pre torch torchvision torchaudio --extra-index-url https://download.pytorch.org/whl/nightly/cpu
Note：检查是否安装成功，首先在命令行输入 python 进入 python 编程环境，然后输入
1
2
3
4
>>> import torch
>>> print(torch.backends.mps.is_available())

True
若输出结果为 Ture，则表明安装成功。
下载 ipykernel 考虑到书中给的代码运行环境是 jupyter，应该此处安装 ipykernel，以确保 jupyter-notebook 中可以使用刚刚安装的 d2l 虚拟环境的内核。
1
2
3
pip install ipykernel

python -m ipykernel install --user --name ENVNAME --display-name DISP_NAME
Note：ENVNAME 和 DISP-NAME 分别为虚拟环境的名字（此处为 d2l）和想要显示的名字。为了简便，此处将两个字段都设置为 d2l。

3.3 安装Pytorch, d2l, jupyter包

第三步，安装深度学习框架和d2l软件包

在安装深度学习框架之前，请先检查你的计算机上是否有可用的GPU（为笔记本电脑上显示器提供输出的GPU不算）。例如，你可以查看计算机是否装有NVIDIA GPU并已安装CUDA。如果你的机器没有任何GPU，没有必要担心，因为你的CPU在前几章完全够用。但是，如果你想流畅地学习全部章节，请提早获取GPU并且安装深度学习框架的GPU版本。
- 你可以按如下方式安装PyTorch的CPU或GPU版本：
  1
  2
  pip install torch==1.8.1
  pip install torchvision==0.9.1
- 也可以访问官网 https://pytorch.org/get-started/locally/ 选择适合自己电脑pytorch版本下载!
- 本课程的jupyter notebook代码详见 https://zh-v2.d2l.ai/d2l-zh.zip
- 下载jupyter notebook ：输入命令 pip install jupyter notebook （若pip失灵可以尝试pip3），输入密命令 jupyter notebook 即可打开。

3.4 总结

本节主要介绍安装Miniconda、CPU环境下的Pytorch和其它课程所需软件包(d2l, jupyter)。对于前面几节来说，CPU已经够用了。
- 如果您已经安装了Miniconda/Anaconda, Pytorch框架和jupyter记事本, 您只需再安装d2l包，就可以跳过本节视频了开启深度学习之旅了; 如果希望后续章节在GPU下跑深度学习, 可以新建环境安装CUDA版本的Pytorch。
- 如果需要在Windows下安装CUDA和Pytorch(cuda版本)，用本地GPU跑深度学习，可以参考李沐老师Windows下安装CUDA和Pytorch跑深度学习，如果网慢总失败的同学可以参考cuda11.0如何安装pytorch？ - Glenn1Q84的回答 - 知乎。当然，如果不方便在本地进行配置(如无GPU, GPU显存过低等)，也可以选择Colab(需要科学上网)，或其它云服务器GPU跑深度学习。

如果pip安装比较慢，可以用镜像源安装：

1	pip install torch torchvision -i http://mirrors.aliyun.com/pypi/simple/ --trusted-host mirrors.aliyun.com

如果安装时经常报错, 可以参考课程评论区部分。

4 数据操作与数据预处理

4.1 数据处理

00:19 N维数组样例

为了能够完成各种数据操作，我们需要某种方法来存储和操作数据。通常，我们需要做两件重要的事：

获取数据；
将数据读入计算机后对其进行处理。

如果没有某种方法来存储数据，那么获取数据是没有意义的。

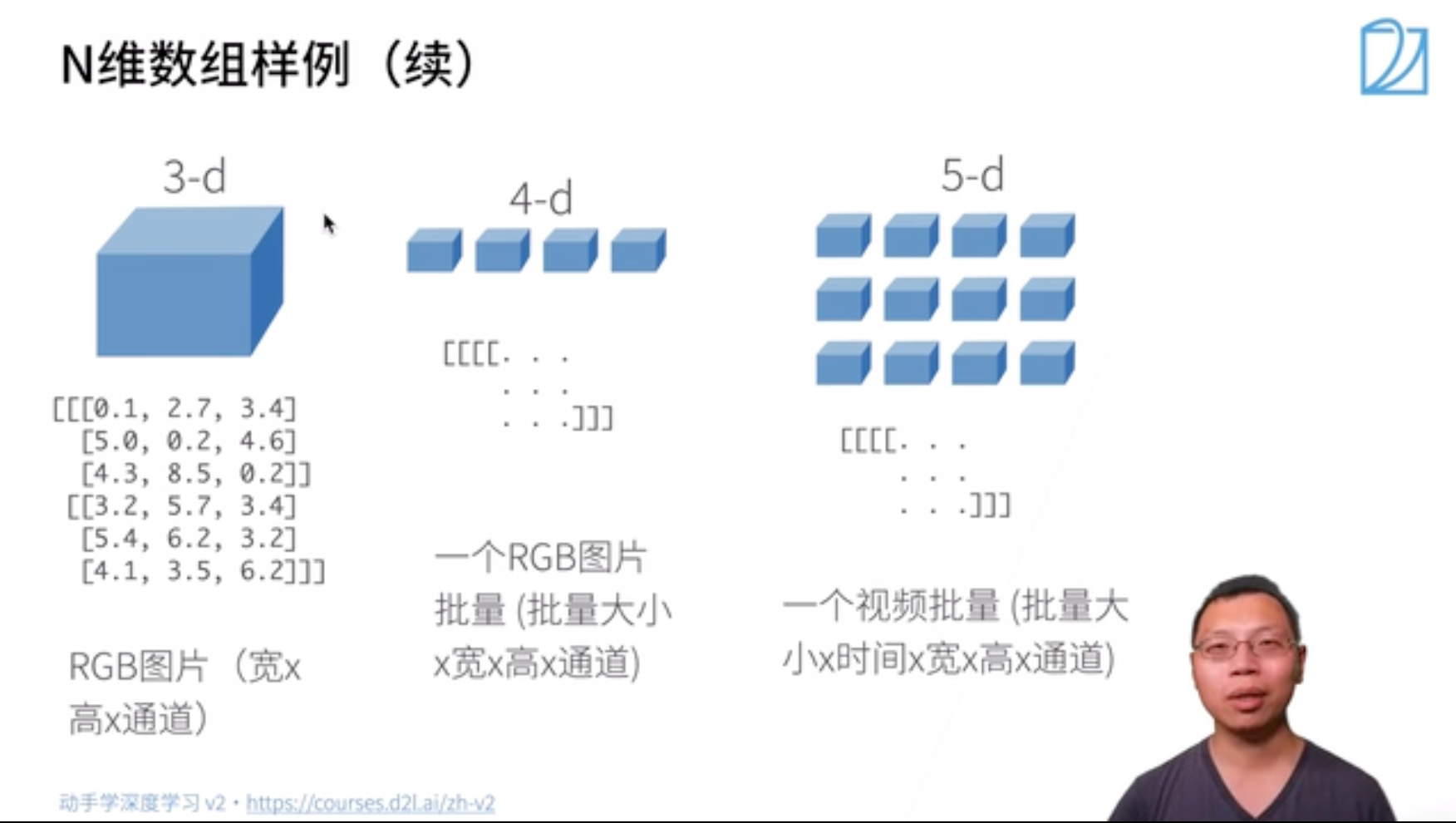
首先，我们介绍 n 维数组，也称为张量（tensor）。PyTorch的张量类与Numpy的ndarray类似。但在深度学习框架中应用PyTorch的张量类，又比Numpy的ndarray多一些重要功能：

tensor可以在很好地支持GPU加速计算，而NumPy仅支持CPU计算；
tensor支持自动微分。

低维数组

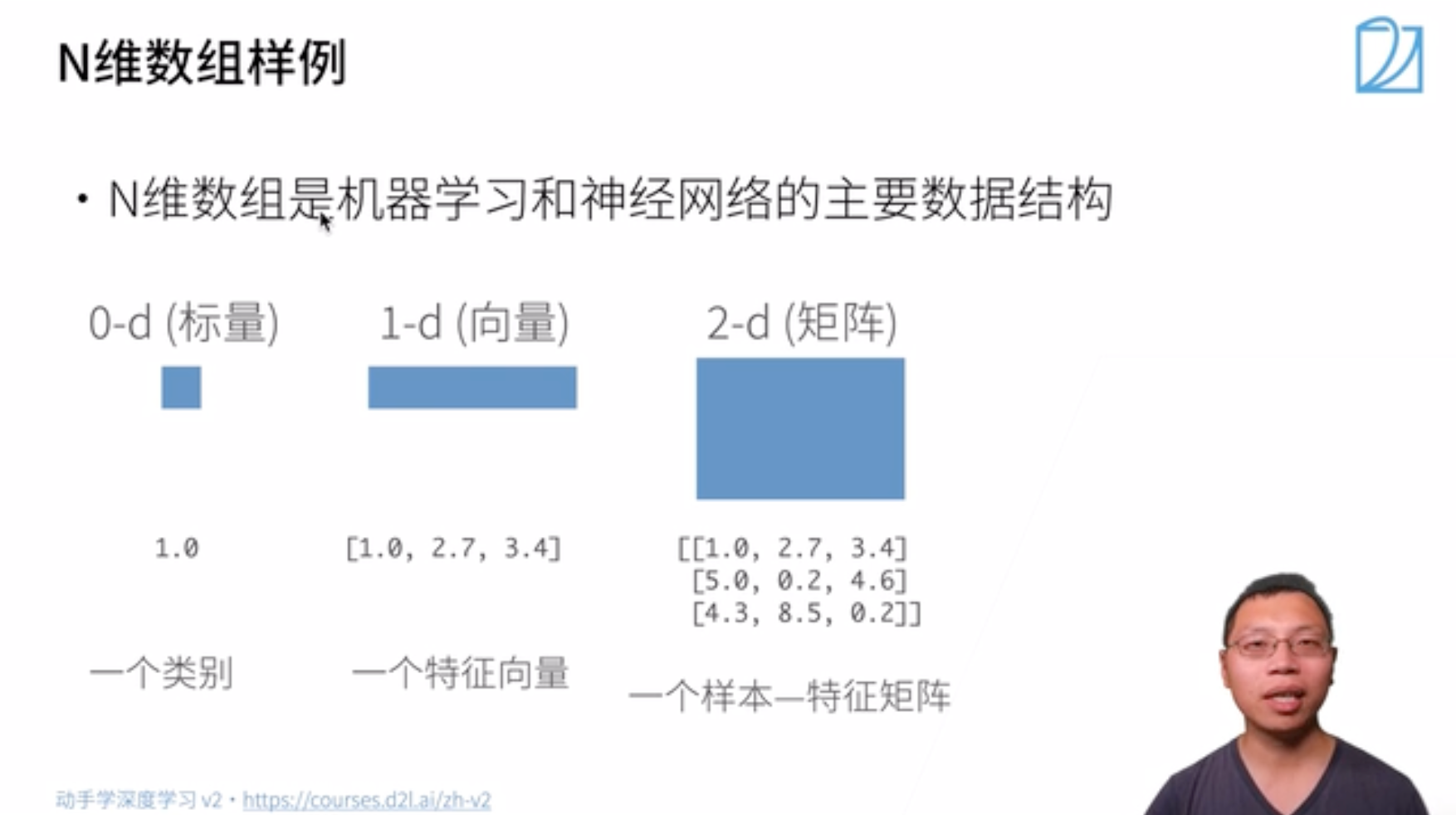
- 高维数组

02:36 创建数组

03:06 访问元素

#### 基本操作

数据操作

张量表示由一些数值组成的数组，这个数组可能有多个维度。

一个轴：对应数学上的向量（vector）；
两个轴：对应数学上的矩阵（matrix）；
两个轴以上：没有特殊的数学名称。

可使用arange创建行向量x，默认创建为浮点数，张量中的每个值都称为张量的元素（element）。

Note：除非额外指定，新的张量默认将存储在内存中，并采用基于CPU的计算。

1 2	>>> x = torch.arange(12) tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])

访问张量的形状

1 2	>>> x.shape # 访问张量的形状 torch.Size([12])

张量的大小

1 2	>>> x.size() # 元素总数 torch.Size([12])

元素个数。在处理更高维度的的张量时，可以用 numel 获取张量中元素的个数。

1 2	>>> x.numel() # number of elements 12

改变张量形状。

>>> X = x.reshape(3, 4)
	tensor([[ 0,  1,  2,  3],
        	[ 4,  5,  6,  7],
        	[ 8,  9, 10, 11]])
    

>>> x.reshape(-1,4)
	tensor([[ 0,  1,  2,  3],
	        [ 4,  5,  6,  7],
	        [ 8,  9, 10, 11]])

常量矩阵

>>> torch.zeros((2, 3, 4))
	tensor([[[0., 0., 0., 0.],
         	 [0., 0., 0., 0.],
         	 [0., 0., 0., 0.]],

        	[[0., 0., 0., 0.],
         	 [0., 0., 0., 0.],
         	 [0., 0., 0., 0.]]])

>>> torch.ones((2, 3, 4))
	tensor([[[1., 1., 1., 1.],
         	 [1., 1., 1., 1.],
         	 [1., 1., 1., 1.]],

        	[[1., 1., 1., 1.],
         	 [1., 1., 1., 1.],
         	 [1., 1., 1., 1.]]])

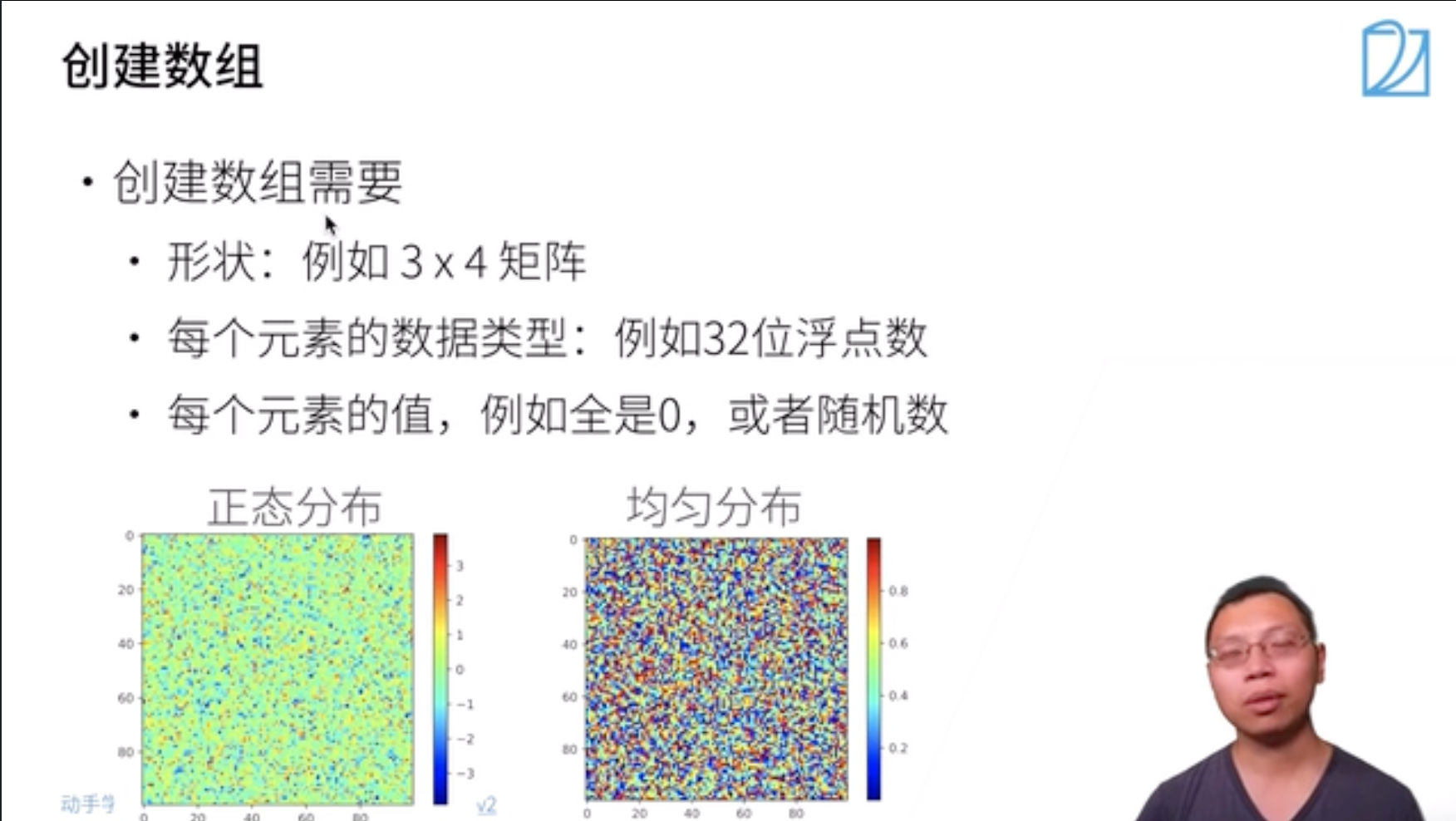
符合某种分布的矩阵。通过从某个特定的概率分布中随机采样来得到张量中每个元素的值。例如，当构造数组来作为神经网络中的参数时，通常会随机初始化参数的值，使得其服从均值为0、标准差为1的标准正态分布。

>>> torch.randn(3, 4)
	tensor([[ 0.1364,  0.3546, -0.9091, -1.8926],
        	[ 0.5786, -0.9019, -0.1305, -0.1899],
        	[ 0.5696,  1.1626, -0.5987,  0.4085]])

基于列表。

>>> torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
	tensor([[2, 1, 4, 3],
        	[1, 2, 3, 4],
        	[4, 3, 2, 1]])

4.2 简单运算

我们想在这些数据上执行数学运算，其中最简单且最有用的操作是按元素（elementwise）运算。我们通过将标量函数升级为按元素向量运算来生成向量值\(F: \mathbb{R}^d, \mathbb{R}^d \rightarrow \mathbb{R}^d\)。

基本运算

>>> x = torch.tensor([1.0, 2, 4, 8])
>>> y = torch.tensor([2, 2, 2, 2])
>>> x + y, x - y, x * y, x / y, x ** y
	(tensor([ 3.,  4.,  6., 10.]),
 	 tensor([-1.,  0.,  2.,  6.]),
 	 tensor([ 2.,  4.,  8., 16.]),
 	 tensor([0.5000, 1.0000, 2.0000, 4.0000]),
 	 tensor([ 1.,  4., 16., 64.]))

指数

1 2	>>> torch.exp(x) tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])

连接。

>>> X = torch.arange(12, dtype=torch.float32).reshape((3,4))
>>> Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
>>> torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
	(tensor([[ 0.,  1.,  2.,  3.],
         	 [ 4.,  5.,  6.,  7.],
         	 [ 8.,  9., 10., 11.],
         	 [ 2.,  1.,  4.,  3.],
         	 [ 1.,  2.,  3.,  4.],
         	 [ 4.,  3.,  2.,  1.]]),
 	 tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],
         	 [ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],
         	 [ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]]))

三维张量连接。由上述例子可见，当需要按轴-x连结两个张量时，我们就在第x+1层括号内将两张量中的元素相组合。类似地，我们将两个三维张量相连结。

>>> X = torch.arange(12, dtype=torch.float32).reshape((3, 2, 2))
>>> Y = torch.tensor([[[2.0, 1], [4, 3]], [[1, 2], [3, 4]], [[4, 3], [2, 1]]])
>>> torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1), torch.cat((X, Y), dim=2)
	(tensor([[[ 0.,  1.],
          	  [ 2.,  3.]],
 
         	 [[ 4.,  5.],
          	  [ 6.,  7.]],
 
         	 [[ 8.,  9.],
          	  [10., 11.]],
 
         	 [[ 2.,  1.],
          	  [ 4.,  3.]],
 
         	 [[ 1.,  2.],
          	  [ 3.,  4.]],
 
         	 [[ 4.,  3.],
          	  [ 2.,  1.]]]),
 	 tensor([[[ 0.,  1.],
          	  [ 2.,  3.],
          	  [ 2.,  1.],
          	  [ 4.,  3.]],
 
         	 [[ 4.,  5.],
          	  [ 6.,  7.],
          	  [ 1.,  2.],
          	  [ 3.,  4.]],
 
         	 [[ 8.,  9.],
         	  [10., 11.],
         	  [ 4.,  3.],
          	  [ 2.,  1.]]]),
 	 tensor([[[ 0.,  1.,  2.,  1.],
          	  [ 2.,  3.,  4.,  3.]],
 
        	 [[ 4.,  5.,  1.,  2.],
          	  [ 6.,  7.,  3.,  4.]],
 
         	 [[ 8.,  9.,  4.,  3.],
         	  [10., 11.,  2.,  1.]]]))

逻辑运算。

>>> X == Y
	tensor([[False,  True, False,  True],
        	[False, False, False, False],
            [False, False, False, False]])

求和。

1 2	>>> X.sum() tensor(66.)

广播机制

07:31 广播机制

在上面的部分中，我们看到了如何在相同形状的两个张量上执行按元素操作。在某些情况下，即使形状不同，我们仍然可以通过调用广播机制（broadcasting mechanism）来执行按元素操作。

这种机制的工作方式如下：首先，通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状。其次，对生成的数组执行按元素操作。在大多数情况下，我们将沿着数组中长度为1的轴进行广播，如下例子：

>>> a = torch.arange(3).reshape((3, 1))
>>> b = torch.arange(2).reshape((1, 2))
>>> a, b, a + b
	(tensor([[0],
         	 [1],
         	 [2]]),
 	 tensor([[0, 1]]))
 	 tensor([[0, 1],
        	 [1, 2],
        	 [2, 3]])

Note：广播机制只能扩展维度，而不能凭空增加张量的维度，例如在计算沿某个轴的均值时，若张量维度不同，则会报错：

1
2
3

>>> C = torch.arange(24, dtype=torch.float32).reshape(2, 3, 4)
>>> C / C.sum(axis=1)
	RuntimeError: The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1

此时我们需要将keepdims设为True，才能正确利用广播机制扩展C.sum(axis=1)的维度：

>>> C.sum(axis = 1).shape,C.sum(axis = 1, keepdims=True).shape
	torch.Size([2, 4]), torch.Size([2, 1, 4])

>>> C / C.sum(axis=1, keepdims=True)
	tensor([[[0.0000, 0.0667, 0.1111, 0.1429],
         	 [0.3333, 0.3333, 0.3333, 0.3333],
         	 [0.6667, 0.6000, 0.5556, 0.5238]],

        	[[0.2500, 0.2549, 0.2593, 0.2632],
         	 [0.3333, 0.3333, 0.3333, 0.3333],
         	 [0.4167, 0.4118, 0.4074, 0.4035]]])

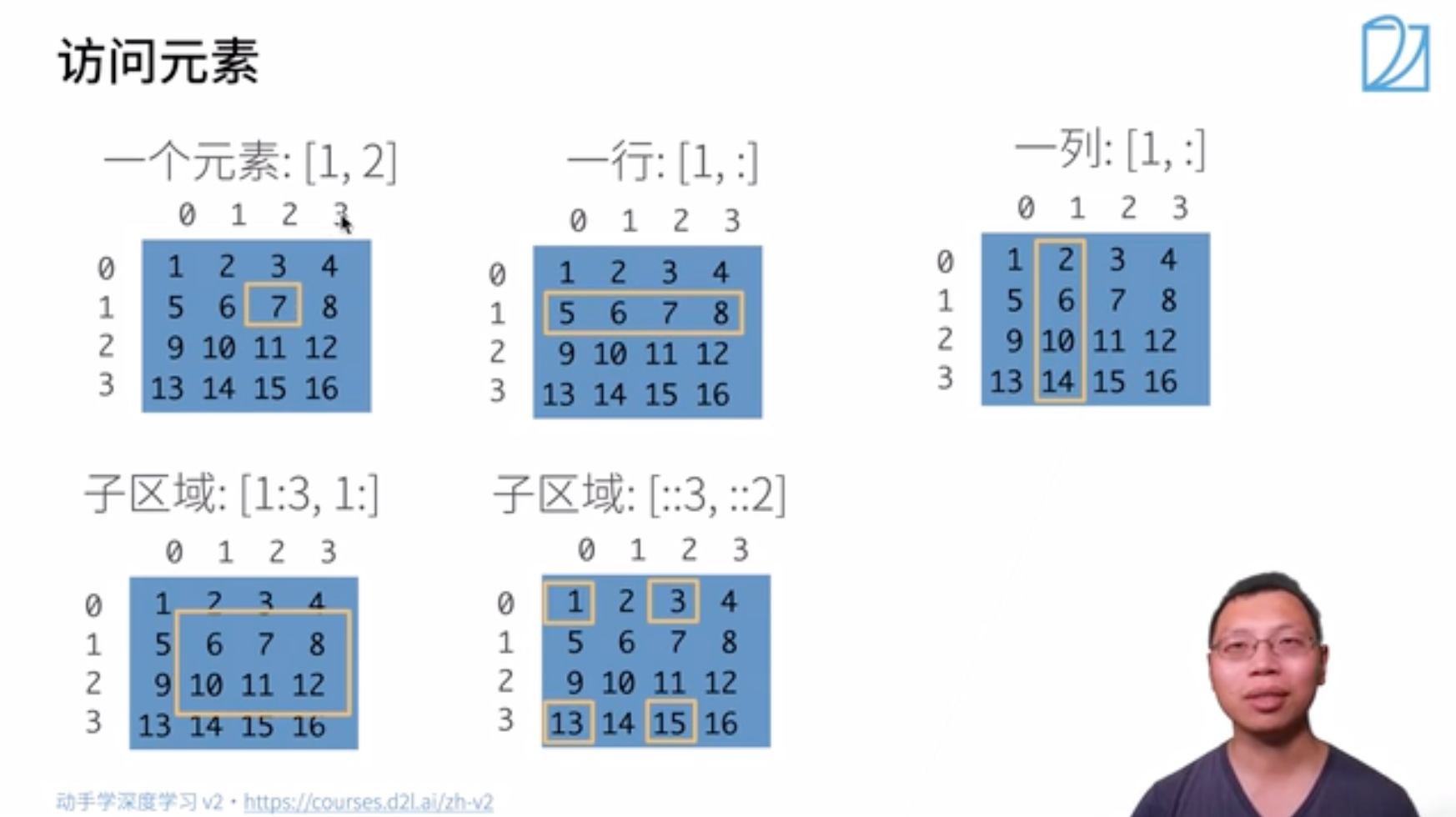
索引和切片

09:34 元素访问

通过索引访问。

>>> X[-1], X[1:3]
	(tensor([ 8.,  9., 10., 11.]),
 	 tensor([[ 4.,  5.,  6.,  7.],
         	 [ 8.,  9., 10., 11.]]))

间隔访问。可以用[::2]每间隔一个元素选择一个元素，可以用[::3]每间隔两个元素选择一个元素：

1
2
3

>>> X[::2, ::3]
	tensor([[ 0.,  3.],
          	[ 8., 11.]])

写入数据。除读取外，我们还可以通过指定索引来将元素写入矩阵。

>>> X[1, 2] = 9
	tensor([[ 0.,  1.,  2.,  3.],
        	[ 4.,  5.,  9.,  7.],
       	 	[ 8.,  9., 10., 11.]])

多元素赋值。

>>> X[0:2, :] = 12
	tensor([[12., 12., 12., 12.],
        	[12., 12., 12., 12.],
       	 	[ 8.,  9., 10., 11.]])

节约内存

10:50 内存管理

如果在后续计算中没有重复使用X，我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。

>>> before = id(X) # 内存地址
>>> X += Y
>>> id(X) == before
	True

转换为 NumPy 对象

将深度学习框架定义的张量转换为NumPy张量（ndarray）。torch张量和numpy数组将共享它们的底层内存，就地操作更改一个张量也会同时更改另一个张量。

>>> A = X.numpy()
>>> B = torch.tensor(A)
>>> type(A), type(B)
	(numpy.ndarray, torch.Tensor)

要(将大小为1的张量转换为Python标量)，我们可以调用item函数或Python的内置函数。

1
2
3

>>> a = torch.tensor([3.5])
>>> a, a.item(), float(a), int(a)
	(tensor([3.5000]), 3.5, 3.5, 3)

4.2 数据预处理

00:08 数据预处理

为了能用深度学习来解决现实世界的问题，我们经常从预处理原始数据开始，而不是从那些准备好的张量格式数据开始。在Python中常用的数据分析工具中，我们通常使用pandas软件包。像庞大的Python生态系统中的许多其他扩展包一样，pandas可以与张量兼容。本节我们将简要介绍使用pandas预处理原始数据，并将原始数据转换为张量格式的步骤。

读取数据集

举一个例子，我们首先(创建一个人工数据集，并存储在CSV（逗号分隔值）文件)../data/house_tiny.csv中。以其他格式存储的数据也可以通过类似的方式进行处理。下面我们将数据集按行写入CSV文件中。

>>> import os
>>> os.makedirs(os.path.join('..', 'data'), exist_ok=True)
>>> data_file = os.path.join('..', 'data', 'house_tiny.csv')
>>> with open(data_file, 'w') as f:
>>>     f.write('NumRooms,Alley,Price\n')  # 列名
>>>     f.write('NA,Pave,127500\n')  # 每行表示一个数据样本
>>>     f.write('2,NA,106000\n')
>>>     f.write('4,NA,178100\n')
>>>     f.write('NA,NA,140000\n')

要从创建的CSV文件中加载原始数据集，我们导入pandas包并调用read_csv函数。该数据集有四行三列。其中每行描述了房间数量（“NumRooms”）、巷子类型（“Alley”）和房屋价格（“Price”）。

1
2
3

>>> import pandas as pd
>>> data = pd.read_csv(data_file)
>>> print(data)

	NumRooms	Alley	Price
0	NaN	Pave	127500
1	2.0	NaN	106000
2	4.0	NaN	178100
3	NaN	NaN	140000

处理缺失值

“NaN”项代表缺失值。**为了处理缺失的数据，典型的方法包括插值法和删除法.

插值法：用一个替代值弥补缺失值；
删除法：直接忽略缺失值。

1
2
3

>>> inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
>>> inputs = inputs.fillna(inputs.mean())
>>> print(inputs)

	NumRooms	Alley
0	3.0	Pave
1	2.0	NaN
2	4.0	NaN
3	3.0	NaN

利用删除法，我们删除缺失元素最多的一个样本。首先，data.isnull()矩阵统计每个元素是否缺失，之后在轴 1 的方向上（对列进行求和）将data.isnull()元素求和，得到每个样本缺失元素个数，取得缺失元素个数最大的样本的序号，并将其删除。

>>> nan_numer = data.isnull().sum(axis=1)
>>> nan_numer
	0    1
	1    1
	2    1
	3    2
	dtype: int64
	
>>> nan_max_id = nan_numer.idxmax()
>>> data_delete = data.drop([nan_max_id], axis=0) # 删除第 nan_max_id 行

	NumRooms	Alley	Price
0	NaN	Pave	127500
1	2.0	NaN	106000
2	4.0	NaN	178100

一般情况下，可以利用dropna删除数据：

1	dropna( axis=0, how=‘any’, thresh=None, subset=None, inplace=False)

Note：

Axis：哪个维度
How：如何删除。any 表示有 nan 即删除，all 表示全为nan删除，Thresh 有多少个nan 删除，Subset 在哪些列中查找nan
Inplace：是否原地修改。

离散值处理

对于类别值或离散值，可以将“NaN”视为一个类别。

1 2	>>> inputs = pd.get_dummies(inputs, dummy_na=True) >>> print(inputs)

	NumRooms	Alley_Pave	Alley_nan
0	3.0	1	0
1	2.0	0	1
2	4.0	0	1
3	3.0	0	1

转换为张量格式

现在所有条目都是数值类型，可以转换为张量格式。

>>> import torch
>>> X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
	(tensor([[3., 1., 0.],
         	 [2., 0., 1.],
         	 [4., 0., 1.],
         	 [3., 0., 1.]], dtype=torch.float64),
 	 tensor([127500, 106000, 178100, 140000]))

4.3 Q&A

07:26 Q&A

Q1：reshape和view的区别？

View为浅拷贝，只能作用于连续型张量；Contiguous函数将张量做深拷贝并转为连续型；Reshape在张量连续时和view相同，不连续时等价于先contiguous再view。

Q2：数组计算吃力怎么办？

学习numpy的知识。

Q3：如何快速区分维度？

利用a.shape或a.dim()。

Q4：Tensor和Array有什么区别？

Tensor是数学上定义的张量，Array是计算机概念数组，但在深度学习中有时将Tensor视为多维数组。

Q5：新分配了y的内存，那么之前y对应的内存会自动释放吗？

Python会在不需要时自动释放内存。

5 线性代数

线性代数

5.1 线性代数基础知识

这部分主要是由标量过渡到向量，再从向量拓展到矩阵操作，重点在于理解矩阵层面上的操作（都是大学线代课的内容，熟悉的可以自动忽略）

标量

#### 2. 向量

3. 矩阵

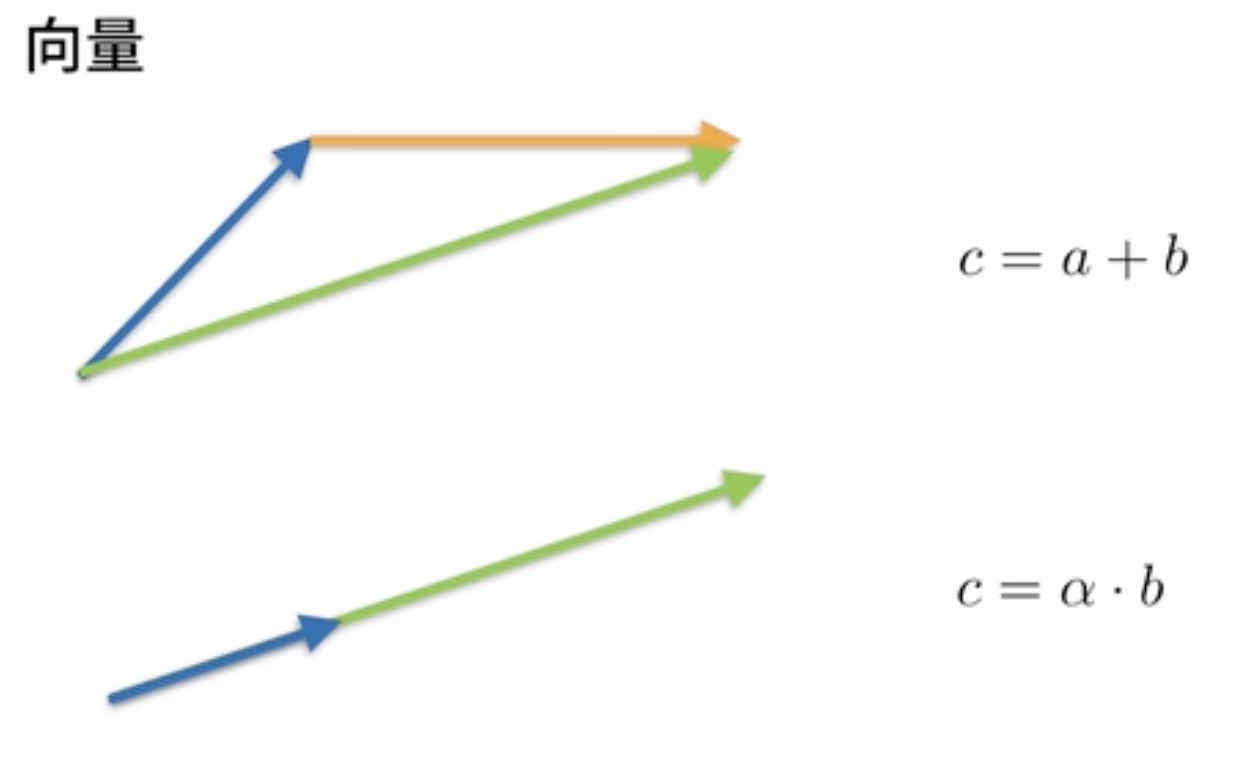
03:49 矩阵

矩阵的操作

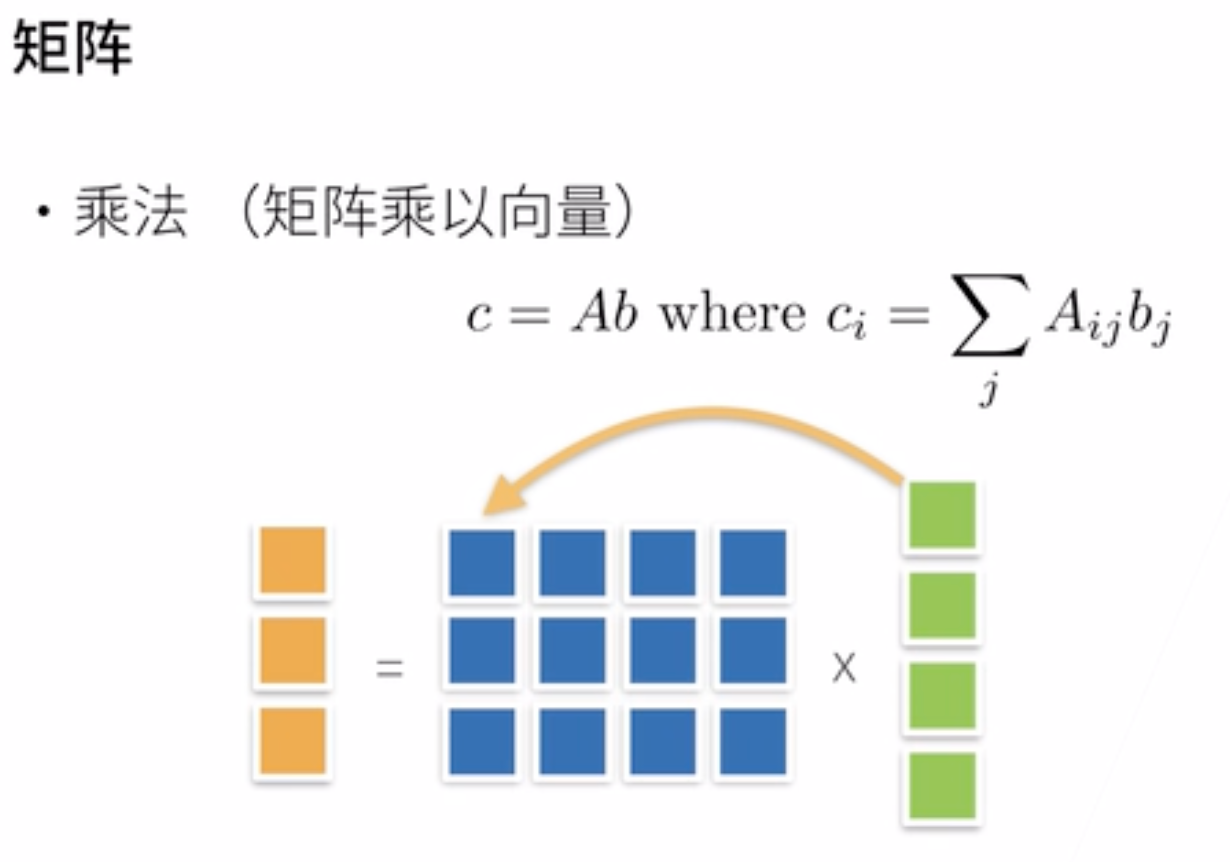
(矩阵范数麻烦且不常用，一般用F范数)

特殊矩阵

(深度学习里基本不会涉及到正定、置换矩阵，这里明确个概念就行)

##### 特征向量和特征值

08:30 特征向量和特征值

数学定义：设 \(A\) 是 \(n\) 阶方阵，如果存在常数 \(\lambda\) 及非零 \(n\) 向量 \(x\)，使得 \(Ax = \lambda x\)，则称 \(\lambda\) 是矩阵 \(A\) 的特征值，\(x\)是 \(A\) 属于特征值 \(\lambda\) 的特征向量。
直观理解：不被矩阵 \(A\) 改变方向（大小改变没关系）的向量 \(x\) 就是A的一个特征向量

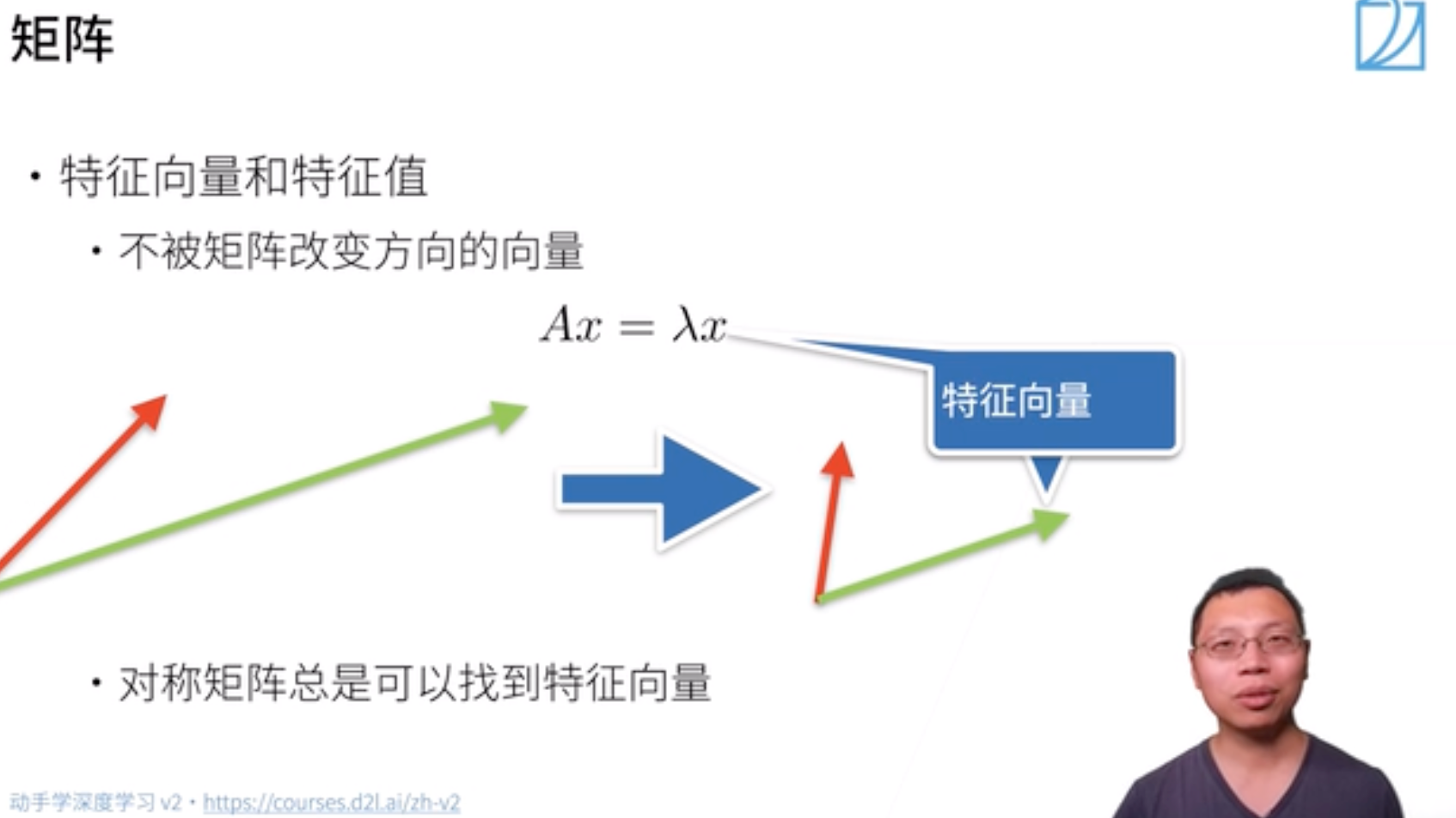
- 矩阵不一定有特征向量，但是对称矩阵总是可以找到特征向量

5.2 线性代数实现

00:09 线性代数实现

这部分主要是应用pytorch实现基本矩阵操作，同样由标量过渡到向量最后拓展到矩阵

标量

import torch    # 应用pytorch框架

# 标量由只有一个元素的张量表示
x = torch.tensor([3.0])     # 单独一个数字表示标量也可以
y = torch.tensor([2.0])     # 单独一个数字表示标量也可以
print(x + y)    # tensor([5.])
print(x * y)    # tensor([6.])
print(x / y)    # tensor([1.5000])
print(x ** y)   # tensor([9.]) 指数运算

2. 向量

# 向量可以看作是若干标量值组成的列表
x = torch.arange(4)     # tensor([0, 1, 2, 3])
                        # 生成[0, 4)范围内所有整数构成的张量tensor
print(x[3])             # tensor(3)
                        # 和列表相似，通过张量的索引访问元素
print(len(x))           # 4
                        # 获取张量x的长度
print(x.shape)          # torch.Size([4])
                        # 获取张量形状，这里x是只有一个轴的张量因此形状只有一个元素

3. 矩阵

创建

A = torch.arange(6)     # tensor([0, 1, 2, 3, 4, 5])
B = torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
C = torch.tensor([[[1,2,3],
                   [4,5,6],
                   [7,8,9]],
                  [[0,0,0],
                   [1,1,1],
                   [2,2,2]]])
D = torch.arange(20, dtype=torch.float32)

转置

A = torch.arange(6)     # tensor([0, 1, 2, 3, 4, 5])
A = A.reshape(3,2)      # tensor([[0, 1],
                        #         [2, 3],
                        #         [4, 5]])

A = A.T                 # 转置 A.T
                        # tensor([[0, 2, 4],
                        #         [1, 3, 5]])

reshape

# 使用reshape方法创建一个形状为3 x 2的矩阵A
A = torch.arange(6)     # tensor([0, 1, 2, 3, 4, 5])
A = A.reshape(3,2)      # tensor([[0, 1],
                        #         [2, 3],
                        #         [4, 5]])

clone

A = torch.arange(20, dtype=torch.float32)
A = A.reshape(5,4)
B = A.clone()   # 通过分配新内存，将A的一个副本分给B，该边B并不影响A的值
print(B)        

'''
tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [12., 13., 14., 15.],
        [16., 17., 18., 19.]])
'''

按元素乘

两个矩阵的按元素乘法称为 哈达玛积 (Hadamard product)，数学符号为 \(\bigodot\)。

>>> A*B

tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [12., 13., 14., 15.],
        [16., 17., 18., 19.]])

sum/mean

A = torch.tensor([[[1,2,3],
                   [4,5,6],
                   [7,8,9]],
                  [[0,0,0],
                   [1,1,1],
                   [2,2,2]]])
print(A.shape)
# torch.Size([2, 3, 3])

print(A.sum())
# tensor(54)

print(A.sum(axis=0))
"""
tensor([[ 1,  2,  3],
        [ 5,  6,  7],
        [ 9, 10, 11]])
"""

print(A.sum(axis=0, keepdims=True))
"""
tensor([[[ 1,  2,  3],
         [ 5,  6,  7],
         [ 9, 10, 11]]])
"""

print(A.sum(axis=1))
"""
tensor([[12, 15, 18],
        [ 3,  3,  3]])
"""

print(A.sum(axis=1, keepdims=True))
"""
tensor([[[12, 15, 18]],

        [[ 3,  3,  3]]])
"""

print(A.sum(axis=2))
"""
tensor([[ 6, 15, 24],
        [ 0,  3,  6]])
"""

print(A.sum(axis=2, keepdims=True)) # 保留维度信息
"""
tensor([[[ 6],
         [15],
         [24]],

        [[ 0],
         [ 3],
         [ 6]]])
"""

print(A.sum(axis=[0,1]))
# tensor([15, 18, 21])

print(A.sum(axis=[0,1], keepdims=True))
# tensor([[[15, 18, 21]]])

cumsum 累加

>>> A, A.cumsum(axis = 1)

(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  1.,  3.,  6.],
         [ 4.,  9., 15., 22.],
         [ 8., 17., 27., 38.],
         [12., 25., 39., 54.],
         [16., 33., 51., 70.]]))

numel

1 2	A = torch.tensor([[0.,0.,0.],[1.,1.,1.]]) print(A.numel()) # 6 元素个数

2.3.7 mean

A = torch.tensor([[0.,0.,0.],[1.,1.,1.]])
print(A.numel())    # 6 元素个数
print(A.sum())      # tensor(3.)
print(A.mean())     # tensor(0.5000)

# 特定轴
A = torch.tensor([[0.,0.,0.],[1.,1.,1.]])
print(A.shape[0])       # 2
print(A.sum(axis=0))    # tensor([1., 1., 1.])
print(A.mean(axis=0))   # tensor([0.5000, 0.5000, 0.5000])	平均值

>>> x = torch.tensor([0.,1.,2.,3.])
>>> y = torch.tensor([1.,1.,1.,1.])
>>> print(torch.dot(x, y))  

tensor(6.)

mm、mv

A = torch.tensor([[0,1,2],
                  [3,4,5]])
B = torch.tensor([[2,2],
                  [1,1],
                  [0,0]])
x = torch.tensor([3,3,3])

print(torch.mv(A, x)) # matrix-vector product 向量积
"""
tensor([ 9, 36])
"""

print(torch.mm(A, B)) # 矩阵积
"""
tensor([[ 1,  1],
        [10, 10]])
"""

L1、L2、F范数

x = torch.tensor([3.0, -4.0])
print(torch.abs(x).sum())   # 向量的L1范数: tensor(7.)  x中的每个元素绝对值的和
print(torch.norm(x))        # 向量的L2范数: tensor(5.)  x中的每个元素平方的和开根号

A = torch.ones((4, 9))
print(torch.norm(A))        # 矩阵的F范数:  tensor(6.)  A中的每个元素平方的和开根号

运算

A = torch.arange(20, dtype=torch.float32)
A = A.reshape(5,4)
B = A.clone()   

print(B)        # tensor([[ 0.,  1.,  2.,  3.],
                #         [ 4.,  5.,  6.,  7.],
                #         [ 8.,  9., 10., 11.],
                #         [12., 13., 14., 15.],
                #         [16., 17., 18., 19.]])
                
print(A == B)
"""
tensor([[True, True, True, True],
        [True, True, True, True],
        [True, True, True, True],
        [True, True, True, True],
        [True, True, True, True]])
"""

print(A + B)
"""
tensor([[ 0.,  2.,  4.,  6.],
        [ 8., 10., 12., 14.],
        [16., 18., 20., 22.],
        [24., 26., 28., 30.],
        [32., 34., 36., 38.]])
"""


print(A * B)
"""
tensor([[  0.,   1.,   4.,   9.],
        [ 16.,  25.,  36.,  49.],
        [ 64.,  81., 100., 121.],
        [144., 169., 196., 225.],
        [256., 289., 324., 361.]])
"""

广播

A = torch.tensor([[1.,2.,3.],
                  [4.,5.,6.]])
B = A.sum(axis=1, keepdims=True)

print(B)
"""
tensor([[ 6.],
        [15.]])
"""

print(A / B)
"""
tensor([[0.1667, 0.3333, 0.5000],
        [0.2667, 0.3333, 0.4000]])
"""

print(A + B)
"""
tensor([[ 7.,  8.,  9.],
        [19., 20., 21.]])
"""

print(A * B)
"""
tensor([[ 6., 12., 18.],
        [60., 75., 90.]])
"""

5.3 按特定轴求和

00:01 按特定轴求和

00:01 Q&A

6 矩阵计算

00:00 矩阵计算

6.1 导数的概念及几何意义

标量导数

导数是切线的斜率

指向值变化最大的方向

亚导数（偏导数）

02:16 亚导数

将导数拓展到不可微的函数，在不可导的点的导数可以用一个范围内的数表示

#### 梯度

03:43 梯度

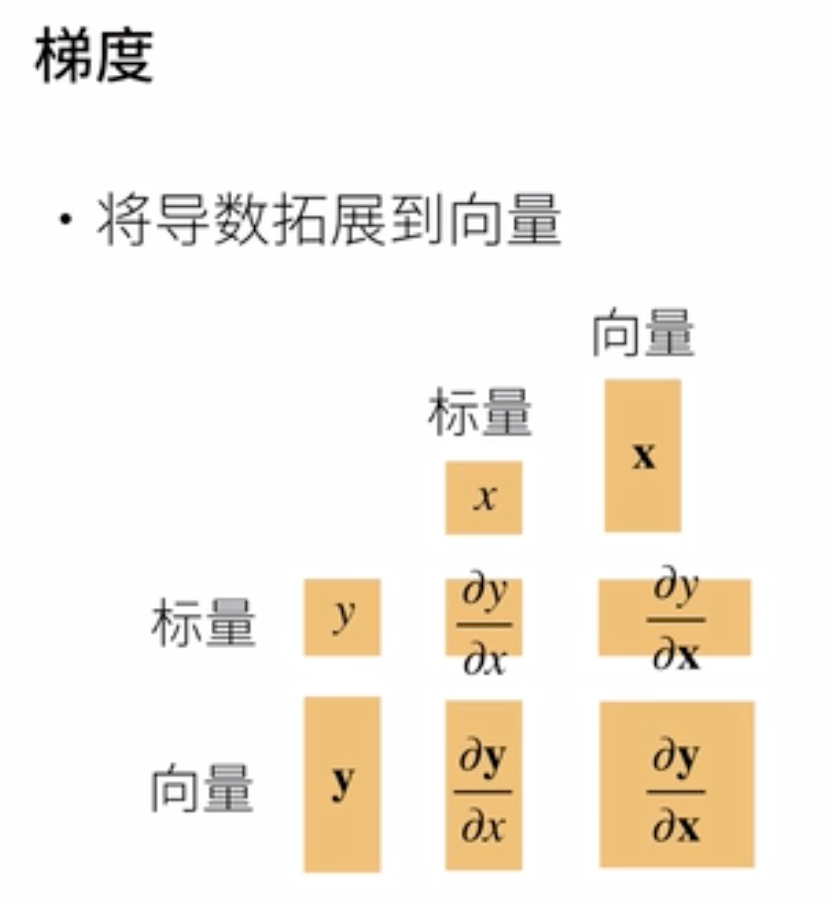
## 6.2 函数与标量，向量，矩阵

该部分结合课程视频和参考文章进行总结（参考了知乎文章：矩阵求导的本质与分子布局、分母布局的本质（矩阵求导——本质篇） - 知乎 (zhihu.com)） - 考虑一个函数 \(\rm{function(input)}\)，针对 \(\rm{function}\) 的类型、输入 \(\rm{input}\) 的类型，可以将函数分为不同的种类：

一、\(\rm{function}\) 为是一个标量

称函数 \(\rm{function}\) 是一个实值标量函数。用细体小写字母 \(f\) 表示。

\(\rm{input}\) 是一个标量。称函数的变元是标量。用细体小写字母 \(x\) 表示。

\[ f(x) = x+2 \]

\(\rm{input}\) 是一个向量。称 \(\rm{function}\) 的变元是向量。用粗体小写字母 \(\boldsymbol{x}\) 表示。

\[ \begin{aligned} \text{设 } \boldsymbol{x} &=\left[x_1, x_2, x_3\right]^T \\ f(\boldsymbol{x})&=a_1 x_1^2+a_2 x_2^2+a_3 x_3^2+a_4 x_1 x_2 \end{aligned} \]

求导：

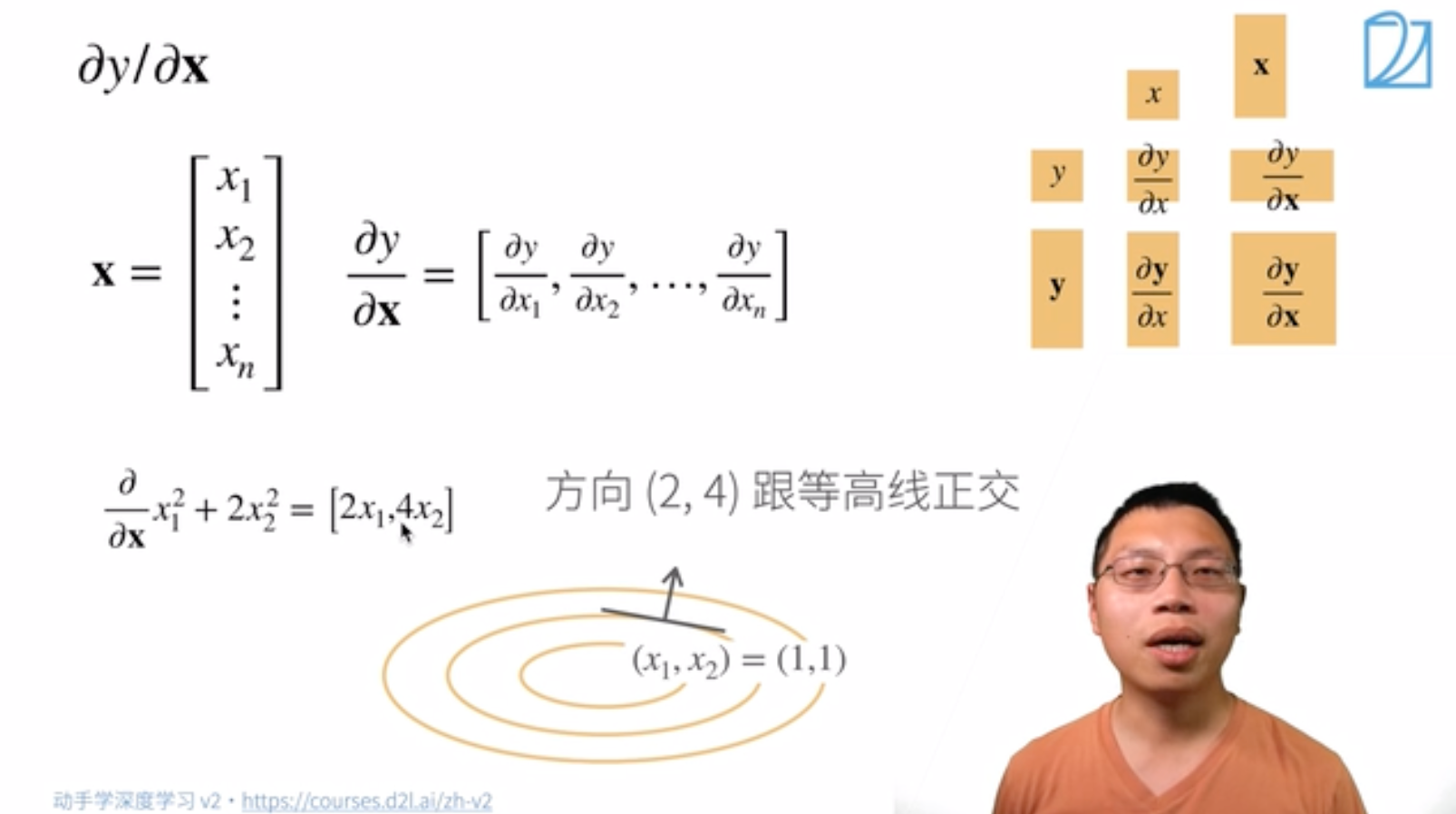
样例：

\(\rm{input}\) 是一个矩阵。称 \(\rm{function}\) 的变元是矩阵。用粗体大写字母 \(\boldsymbol{X}\) 表示。

$$
 \begin{aligned}
 \text{设 } \boldsymbol{X}_{3 \times 2} & =  \left(x_{i j}\right)_{i=1, j=1}^{3,2} \\
 f(\boldsymbol{X}) &=a_1 x_{11}^2+a_2 x_{12}^2+a_3 x_{21}^2+a_4 x_{22}^2+a_5 x_{31}^2+a_6 x_{32}^2
 \end{aligned}

二、\(\rm{function}\) 为是一个向量

称函数 \(\rm{function}\) 是一个实向量函数。用粗体小写字母 \(\boldsymbol{f}\) 表示。

含义：\(\boldsymbol{f}\) 是由若干个 \(f\) 组成的一个向量。

\(\rm{input}\) 是标量。08:39

\[ f_{3 \times 1}(x)=\left[\begin{array}{l} f_1(x) \\ f_2(x) \\ f_3(x)\end{array}\right]=\left[\begin{array}{c} x+1 \\ 2 x+1 \\ 3 x^2+1 \end{array}\right] \]

求导：

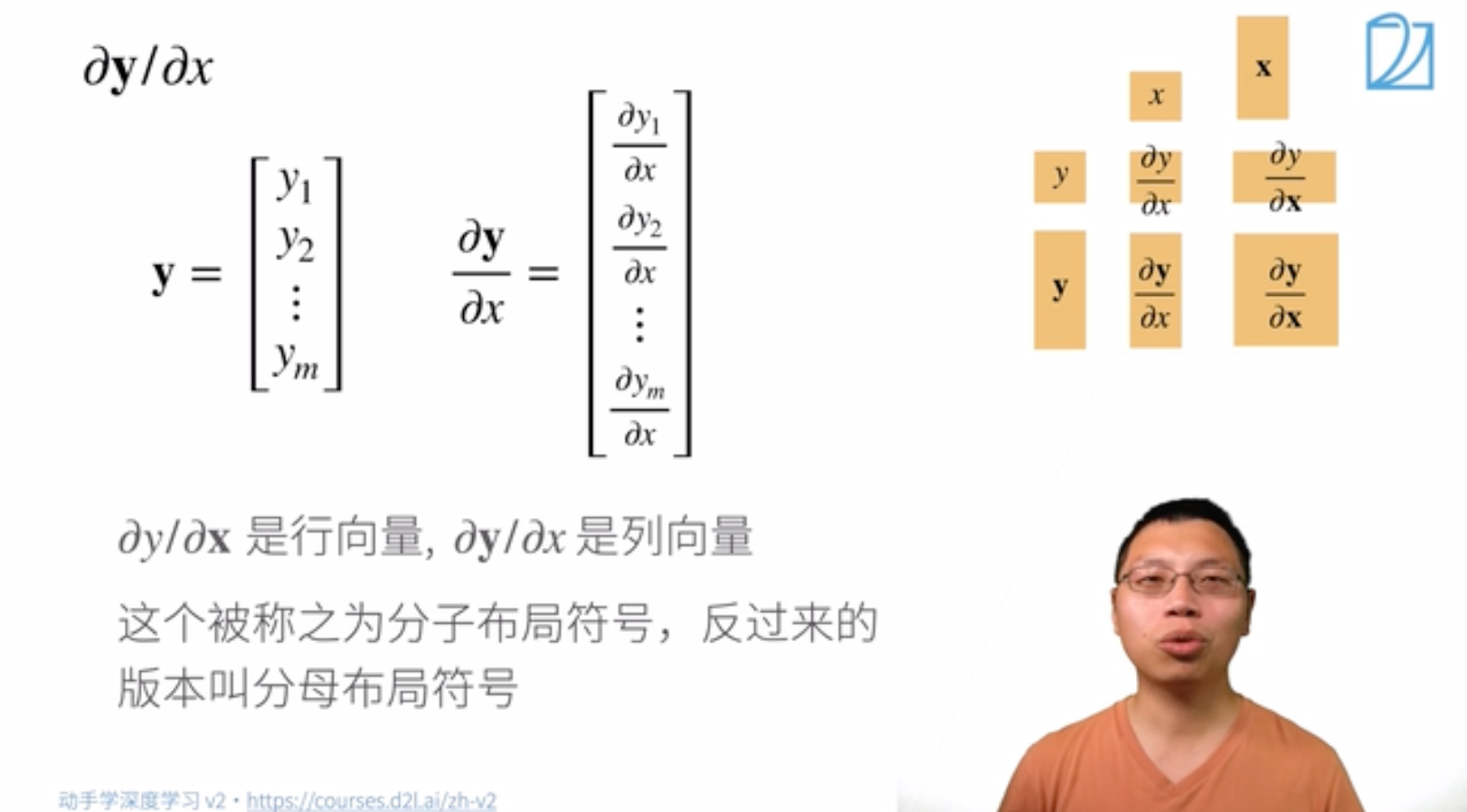
称之为分子布局符号，反过来称为坟墓布局符号。
\(\rm{input}\) 是向量。09:15

称 \(\rm{function}\) 的变元是向量。用粗体小写字母 \(\boldsymbol{x}\) 表示。

\[ \begin{aligned} \boldsymbol{f}_{3 \times 1}(\boldsymbol{x}) =\left[\begin{array}{c} f_1(\boldsymbol{x}) \\ f_2(\boldsymbol{x}) \\ f_3(\boldsymbol{x})\end{array}\right]=\left[\begin{array}{c} x_1+x_2+x_3 \\ x_1^2+2 x_2+2 x_3 \\ x_1 x_2+x_2+x_3 \end{array}\right] \end{aligned} \]

求导：

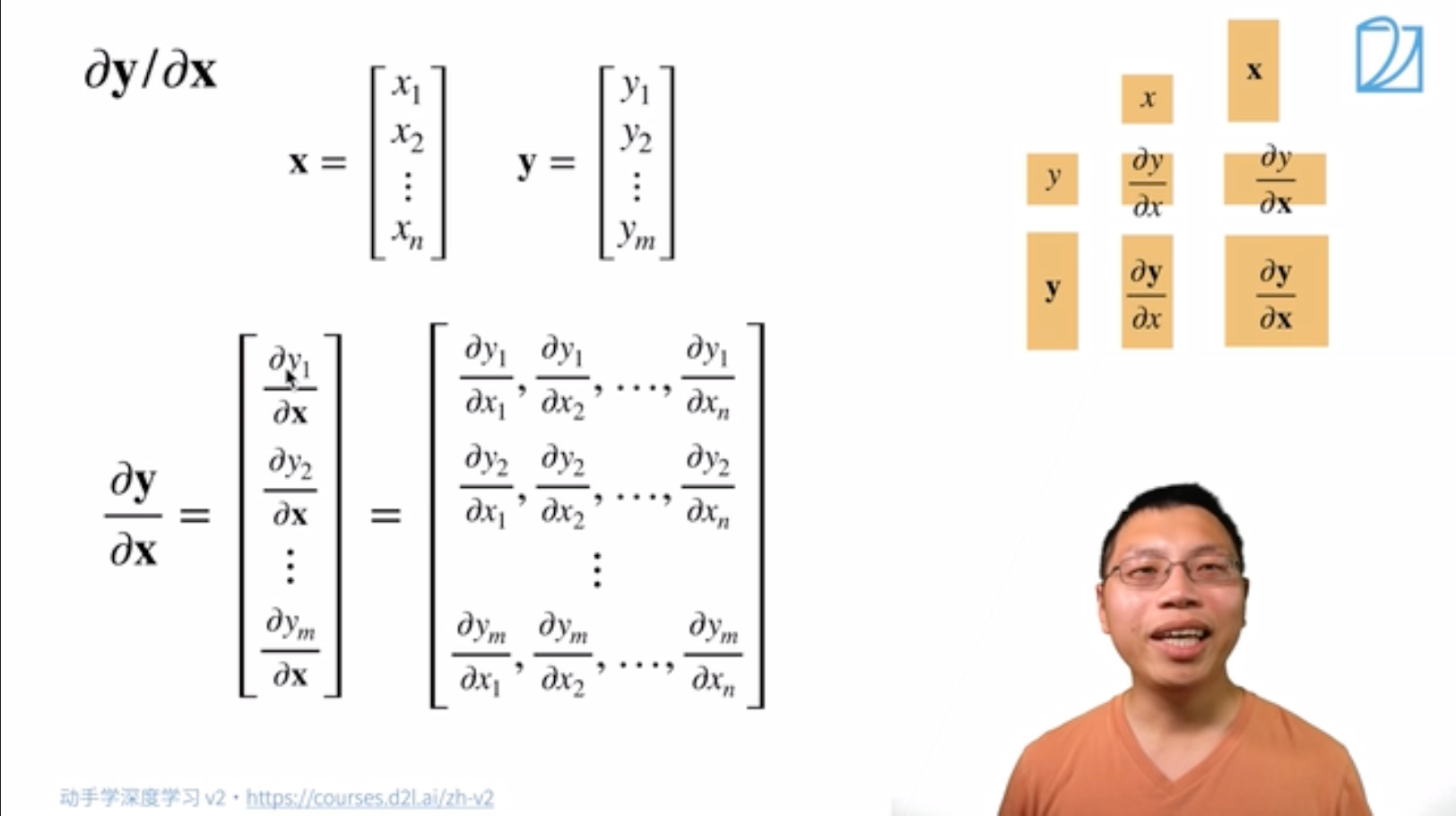
样例：
\(\rm{input}\) 是矩阵。

\[ \boldsymbol{f}_{3 \times 1}(\boldsymbol{X})=\left[\begin{array}{l} f_1(\boldsymbol{X}) \\ f_2(\boldsymbol{X}) \\ f_3(\boldsymbol{X}) \end{array} \right]=\left[\begin{array}{c}x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} \\ x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11} x_{12} \\2x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11} x_{12} \end{array}\right] \]

三、\(\rm{function}\) 为是一个矩阵

称函数 \(\rm{function}\) 是一个实矩阵函数。用粗体大写字母 \(\boldsymbol{F}\) 表示。含义：\(\boldsymbol{F}\) 是由若干个 \(f\) 组成的一个矩阵。

\(\rm{input}\) 是标量。

\[ \boldsymbol{F}_{3 \times 2}(x)=\left[\begin{array}{ll} f_{11}(x) & f_{12}(x) \\ f_{21}(x) & f_{22}(x) \\ f_{31}(x) & f_{32}(x) \end{array}\right]=\left[\begin{array}{cc} x+1 & 2 x+2 \\ x^2+1 & 2 x^2+1 \\ x^3+1 & 2 x^3+1 \end{array}\right] \]

\(\rm{input}\) 是一个向量。称 \(\rm{function}\) 的变元是向量。用粗体小写字母 \(\boldsymbol{x}\) 表示。

\[ \boldsymbol{F}_{3 \times 2}(\boldsymbol{x})=\left[\begin{array}{ll} f_{11}(\boldsymbol{x}) & f_{12}(\boldsymbol{x}) \\ f_{21}(\boldsymbol{x}) & f_{22}(\boldsymbol{x}) \\ f_{31}(\boldsymbol{x}) & f_{32}(\boldsymbol{x}) \end{array}\right]=\left[\begin{array}{cc} 2 x_1+x_2+x_3 & 2 x_1+2 x_2+x_3 \\ 2 x_1+2 x_2+x_3 & x_1+2 x_2+x_3 \\ 2 x_1+x_2+2 x_3 & x_1+2 x_2+2 x_3 \end{array}\right] \]

\(\rm{input}\) 是矩阵。

\[ \begin{aligned} \boldsymbol{F}_{3 \times 2}(\boldsymbol{X}) & =\left[\begin{array}{ll} f_{11}(\boldsymbol{X}) & f_{12}(\boldsymbol{X}) \\ f_{21}(\boldsymbol{X}) & f_{22}(\boldsymbol{X}) \\ f_{31}(\boldsymbol{X}) & f_{32}(\boldsymbol{X}) \end{array}\right] \\ &= {\left[\begin{array}{ll}x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} & 2 x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} \\ 3 x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} & 4 x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} \\ 5 x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} & 6 x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} \end{array}\right] } \end{aligned} \]

求导：

#### 求导的本质

对于一个多元函数： \[ f\left(x_1, x_2, x_3\right)=x_1^2+x_1 x_2+x_2 x_3 \] 可以将 \(f\) 对 \(x_1\)，\(x_2\)，\(x_3\) 的偏导分别求出来，即 \[ \left\{\begin{aligned} \frac{\partial f}{\partial x_1} & =2 x_1+x_2 \\ \frac{\partial f}{\partial x_2} & =x_1+x_3 \\ \frac{\partial f}{\partial x_3} & =x_2 \end{aligned}\right. \] 矩阵求导也是一样的，本质就是 \(\rm{function}\) 中的每个 \(f\) 分别对变元中的每个元素逐个求偏导，只不过写成了向量、矩阵形式而已。 \[ \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}_{3 \times 1}}=\left[\begin{array}{c} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \frac{\partial f}{\partial x_3} \end{array}\right]=\left[\begin{array}{c} 2 x_1+x_2 \\ x_1+x_3 \\ x_2 \end{array}\right] \] 也可以按照 行向量形式展开： \[ \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}_{3 \times 1}^T}=\left[\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \frac{\partial f}{\partial x_3}\right]=\left[2 x_1+x_2, x_1+x_3, x_2\right] \] X为矩阵时，先把矩阵变元 \(\boldsymbol{X}\) 进行转置，再对转置后的每个位置的元素逐个求偏导，结果布局和转置布局一样。 \[ \begin{aligned} \mathrm{D}_{\boldsymbol{X}} f(\boldsymbol{X})= & \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}_{m \times n}^T} \\ & =\left[\begin{array}{cccc} \frac{\partial f}{\partial x_{11}} & \frac{\partial f}{\partial x_{21}} & \cdots & \frac{\partial f}{\partial x_{11}} \\ \frac{\partial f}{\partial x_{12}} & \frac{\partial f}{\partial x_{22}} & \cdots & \frac{\partial f}{\partial x_{m 2}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial f}{\partial x_{1 n}} & \frac{\partial f}{\partial x_{2 n}} & \cdots & \frac{\partial f}{\partial x_{m n}} \end{array}\right]_{n \times m} \end{aligned} \] - 所以，如果 \(\rm{function}\) 中有 \(m\) 个\(f\) (标量)，变元中有 \(n\) 个元素，那么，每个 \(f\) 对变元中的每个元素逐个求偏导后，我们就会产生 \(m \times n\) 个结果。

6.3 矩阵求导的布局

经过上述对求导本质的推导，关于矩阵求导的问题，实质上就是对求导结果的进一步排布问题

对于2.2（\(f\)为向量，\(\rm{input}\)也为向量）中的情况，其求导结果有两种排布方式，一种是分子布局，一种是分母布局

分子布局。就是分子是列向量形式，分母是行向量形式（课上讲的） \[ \frac{\partial \boldsymbol{f}_{2 \times 1}(\boldsymbol{x})}{\partial \boldsymbol{x}_{3 \times 1}^T}=\left[\begin{array}{lll} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \frac{\partial f_1}{\partial x_3} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \frac{\partial f_2}{\partial x_3} \end{array}\right]_{2 \times 3} \]
分母布局，就是分母是列向量形式，分子是行向量形式

\[ \frac{\partial \boldsymbol{f}_{2 \times 1}^T(\boldsymbol{x})}{\partial \boldsymbol{x}_{3 \times 1}}=\left[\begin{array}{ll} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_2}{\partial x_1} \\ \frac{\partial f_1}{\partial x_2} & \frac{\partial f_2}{\partial x_2} \\ \frac{\partial f_1}{\partial x_3} & \frac{\partial f_2}{\partial x_3} \end{array}\right]_{3 \times 2} \]

将求导推广到矩阵，由于矩阵可以看作由多个向量所组成，因此对矩阵的求导可以看作先对每个向量进行求导，然后再增加一个维度存放求导结果。

例如当 \(F\) 为矩阵，\(\rm{input}\) 为矩阵时，\(F\) 中的每个元素 \(f(\text{标量})\) 求导后均为一个矩阵（按照课上的展开方式），因此每个 \(f\)（包含多个 \(f(\text{标量})\)）求导后为存放多个矩阵的三维形状，再由于矩阵 \(F\) 由多个 \(f\) 组成，因此F求导后为存放多个 \(f\) 求导结果的四维形状。

对于不同 \(f\) 和 \(\rm{input}\) 求导后的维度情况总结如下图所示：

## 6.4 Q&A

00:00 Q&A

7 自动求导

7.1 向量链式法则

00:00 自动求导

标量链式法则

\[ y=f(u), u=g(x) \quad \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u} \frac{\partial u}{\partial x} \]

拓展到向量
需要注意维数的变化

下图三种情况分别对应：
1. y为标量，x为向量
2. y为标量，x为矩阵
3. y、x为矩阵

链式法则示例

01:30 链式法则示例

标量对向量求导

这里应该是用分子布局，所以是X转置
涉及到矩阵的情况

X是mxn的矩阵,w为n维向量，y为m维向量； z对Xw-y做L2 norm,为标量；过程与例一大体一致；

Note：由于在神经网络动辄几百层，手动进行链式求导是很困难的，因此我们需要借助自动求导

7.2 自动求导

04:20 自动求导

含义：计算一个函数在指定值上的导数。它有别于：

符号求导
数值求导

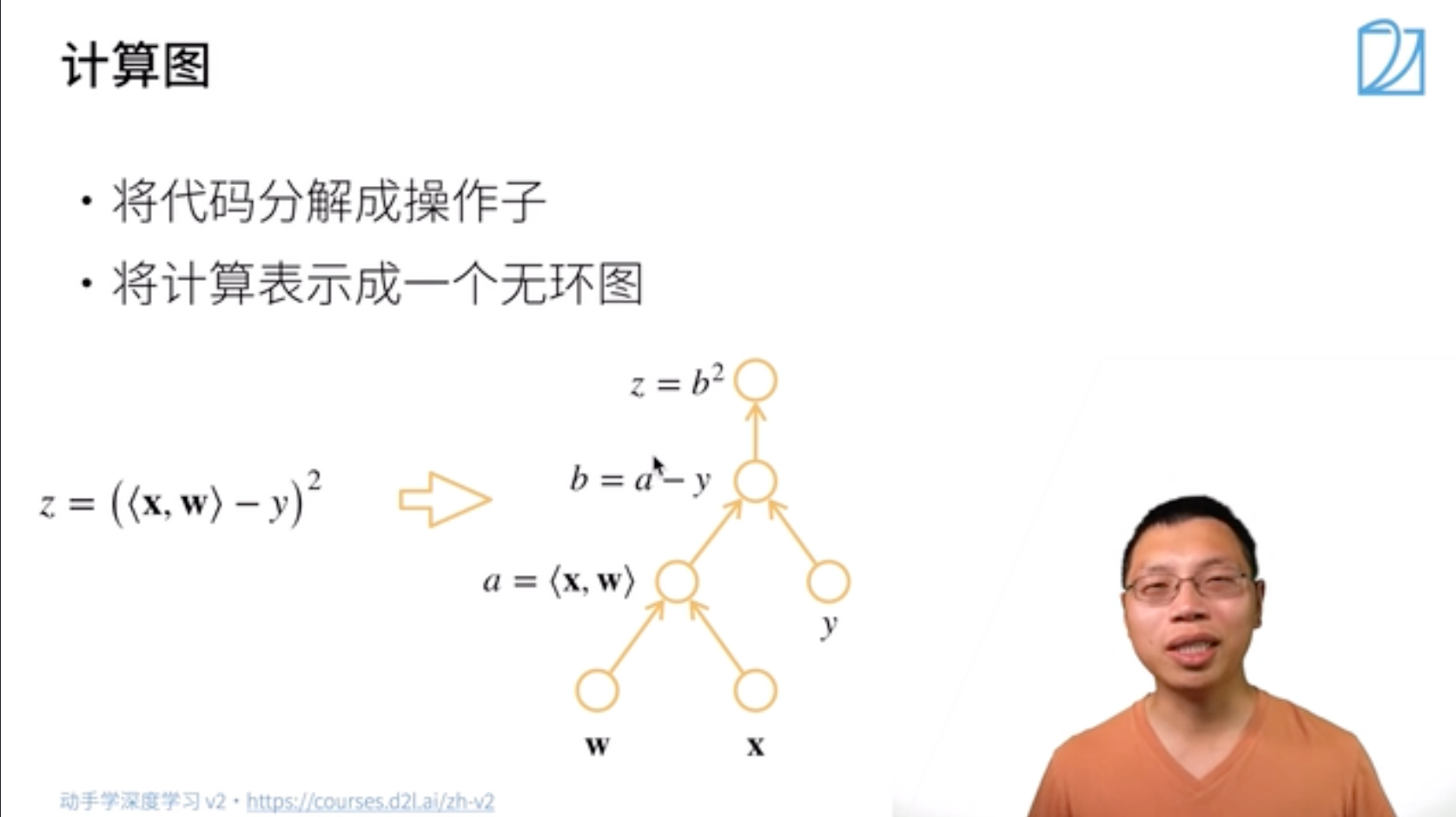
一、计算图

05:11 自动求导

一、步骤： - 将代码分解成操作子 - 将计算表示成一个无环图

下图自底向上其实就类似于链式求导过程：

二、计算图有两种构造方式

显示构造

可以理解为先定义公式再代值

Tensorflow/Theano/MXNet

from mxnet import sym

a = sym.var()
b = sym.var()
c = 2 * a + b
# bind data into a and b later

隐式构造

系统将所有的计算记录下来

Pytorch/MXNet

from mxnet import autograd, nd

with autograd.record():
	a = nd.ones((2, 1))
	b = nd.ones((2, 1))
	c = 2 * a + b

二、自动求导的两种模式

07:39 自动求导的两种模式

- 链式法则：

$$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n} \frac{\partial u_n}{\partial u_{n-1}} \ldots \frac{\partial u_2}{\partial u_1} \frac{\partial u_1}{\partial x}$$

正向累积

\[ \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}\left(\frac{\partial u_n}{\partial u_{n-1}}\left(\cdots\left(\frac{\partial u_2}{\partial u_1} \frac{\partial u_1}{\partial x}\right)\right)\right) \]
反向累积（反向传递back propagation）

\[ \frac{\partial y}{\partial x}=\left(\left(\left(\frac{\partial y}{\partial u_n} \frac{\partial u_n}{\partial u_{n-1}}\right) \ldots\right) \frac{\partial u_2}{\partial u_1}\right) \frac{\partial u_1}{\partial x} \]

反向累积计算过程

09:01反向传递

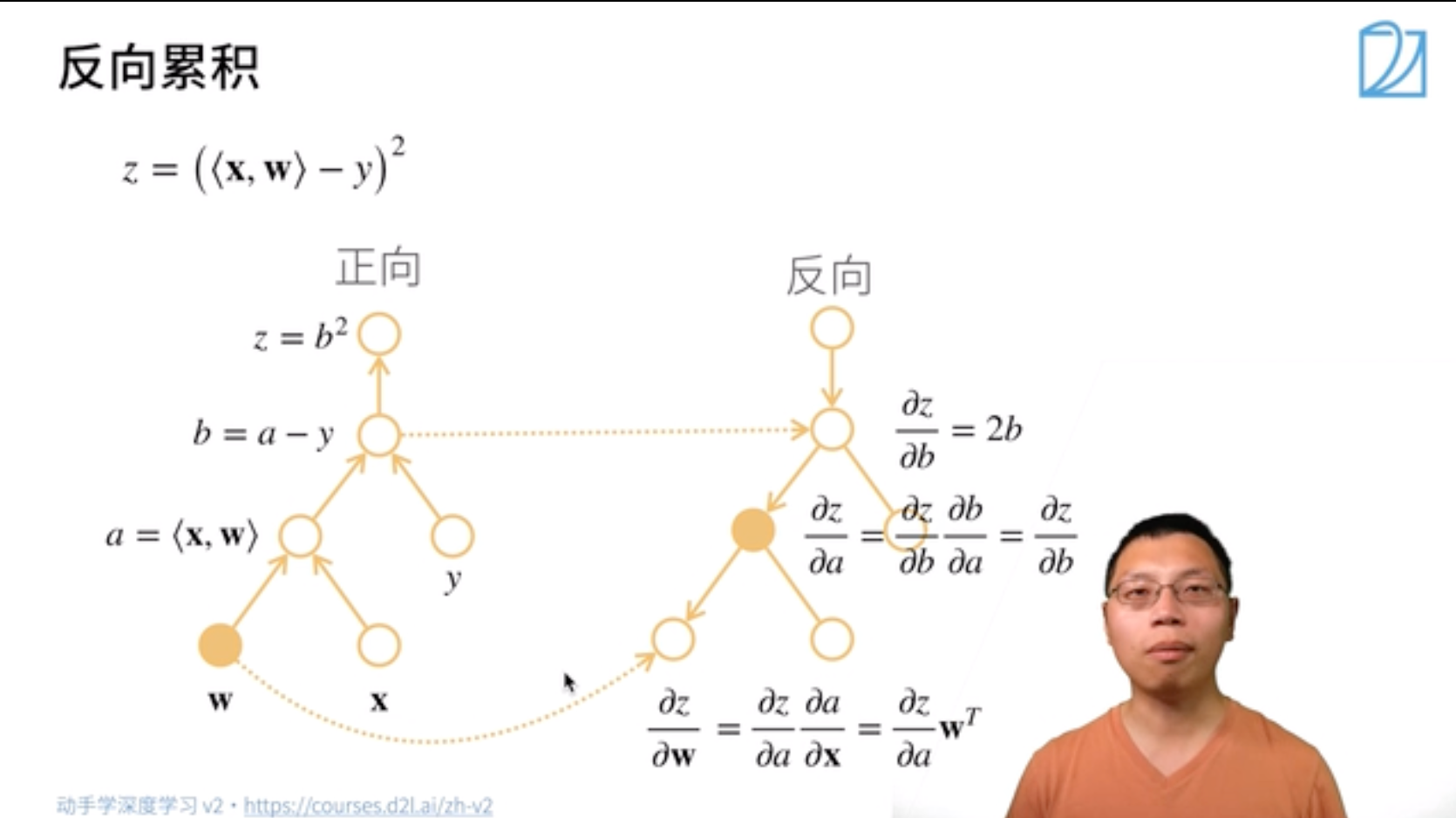
注：

反向累积的正向过程：自底向上，需要存储中间结果反向累积的反向过程：自顶向下，可以去除不需要的枝（图中的x应为w）

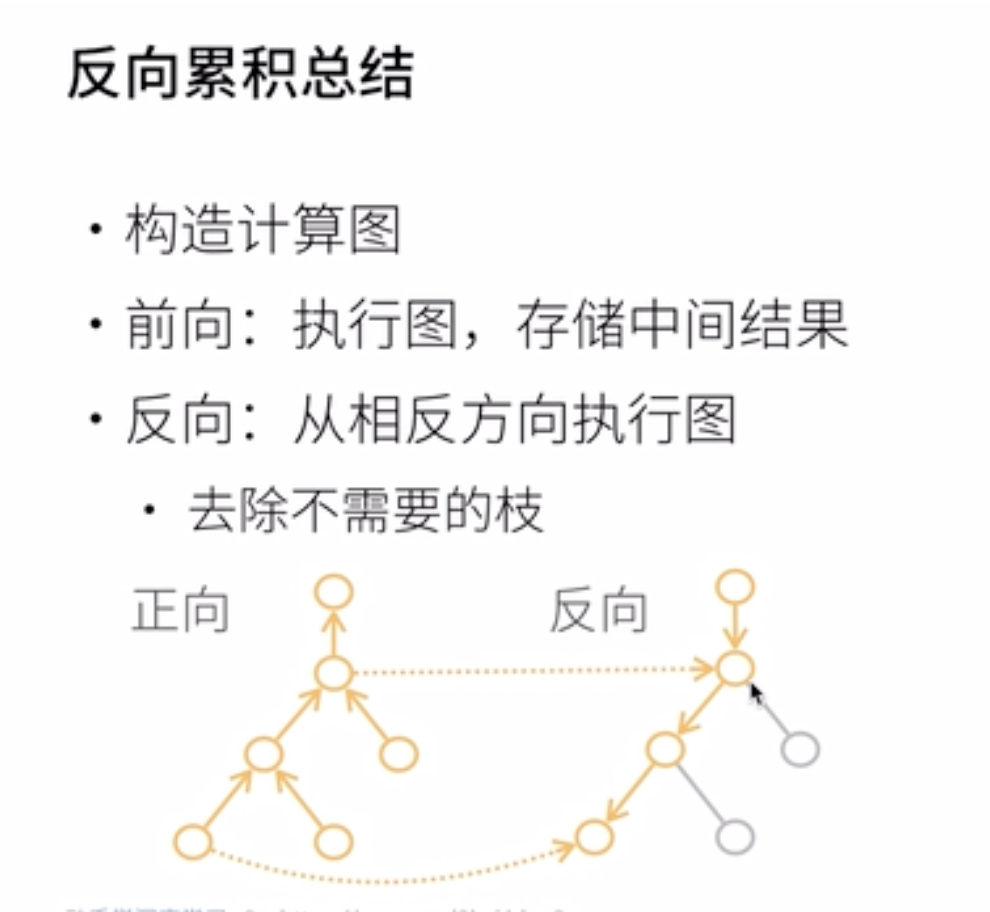
#### 三、复杂度比较

反向累积
- 时间复杂度：\(O(n)\),\(n\)是操作子数
  - 通常正向和反向的代价类似
- 内存复杂度：\(O(n)\)
  - 存储正向过程所有的中间结果
正向累积
每次计算一个变量的梯度时都需要将所有节点扫一遍
- 时间复杂度：\(O(n)\)
- 内存复杂度：\(O(1)\)

7.3 代码部分

00:03 自动求导代码实现

对 y = x.T x 关于列向量x求导

# 对y = x.Tx关于列向量x求导  
>>> import torch 
>>> x = torch.arange(4.0)  
>>> x

tensor([0., 1., 2., 3.])

存储梯度

#存储梯度
>>> x.requires_grad_(True)#等价于x = torch.arange(4.0,requires_grad=True)
>>> x.grad#默认值是None


>>> y = torch.dot(x,x)
>>> y
# PyTorch隐式地构造计算图，grad_fn用于记录梯度计算

tensor(14., grad_fn=<DotBackward0>)

通过调用反向传播函数来自动计算 \(y\) 关于 \(x\) 每个分量的梯度

>>> y.backward()
>>> x.grad

tensor([0., 2., 4., 6.])

验证：

1
2
3

>>> x.grad==2*x # 验证

tensor([True, True, True, True])

在默认情况下，PyTorch会累积梯度，我们需要清除之前的值：

x.grad.zero_() 
# 如果没有上面这一步，结果就会加累上之前的梯度值，变为[1,3,5,7]
y = x.sum()
y.backward()
x.grad

Result：

1	tensor([1., 1., 1., 1.])

哈达玛积 (Hadamard product)

1 2	>>> x.grad.zero_() >>> y=x*x # 哈达玛积，对应元素相乘

上述哈达玛积得到的 \(y\) 是一个向量，此时对 \(x\) 求导得到的是一个矩阵。但是在深度学习中我们一般不计算微分矩阵，而是计算批量中每个样本单独计算的偏导数之和，如下：

>>> y.sum().backward() # 等价于y.backword(torch.ones(len(x)))
>>> x.grad

tensor([0., 2., 4., 6.])

将某些计算移动到记录的计算图之外。03:53。

后可用于用于将神经网络的一些参数固定住

# 后可用于用于将神经网络的一些参数固定住
x.grad.zero_()
y = x*x
u = y.detach()#把y当作常数
z = u*x

z.sum().backward()
x.grad == u

Results:

1	tensor([True, True, True, True])

控制流。05:26

即使构建函数的计算图需要用过Python控制流，仍然可以计算得到的变量的梯度。这也是隐式构造的优势，因为它会存储梯度计算的计算图，再次计算时执行反向过程就可以

def f(a):
    b = a * 2
    while b.norm()<1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(),requires_grad=True)
d = f(a)
d.backward()

a.grad == d / a

Results:

1	tensor(True)

7.3 Q&A

00:00 Q&A

Q1：ppt上隐式构造和显式构造看起来为啥差不多？

显式和隐式的差别其实就是数学上求梯度和python求梯度计算上的差别，不用深究

显式构造就是我们数学上正常求导数的求法，先把所有求导的表达式选出来再代值

Q2:需要正向和反向都算一遍吗？

需要正向先算一遍，自动求导时只进行反向就可以，因为正向的结果已经存储

Q3:为什么PyTorch会默认累积梯度

便于计算大批量；方便进一步设计

Q4:为什么深度学习中一般对标量求导而不是对矩阵或向量求导

loss一般都是标量

Q5:为什么获取.grad前需要backward

相当于告诉程序需要计算梯度，因为计算梯度的代价很大，默认不计算

Q6:pytorch或mxnet框架设计上可以实现矢量的求导吗

可以

0. Preface

1 课程安排

1.1 课程目标

1.2 内容

1.3 学到什么

1.4 基本要求

1.5 课程资源

2 深度学习介绍

2.1 概述

AI地图解读

2.2 深度学习的应用

2.3 总结

3 安装

3.1 安装python

3.2安装Miniconda/Anaconda

2.2 Miniconda环境配置

3.3 安装Pytorch, d2l, jupyter包

3.4 总结

4 数据操作与数据预处理

4.1 数据处理

4.2 简单运算

广播机制

索引和切片

节约内存

转换为 NumPy 对象

4.2 数据预处理

读取数据集

处理缺失值

离散值处理

转换为张量格式

4.3 Q&A

5 线性代数

5.1 线性代数基础知识

标量

3. 矩阵

矩阵的操作

特殊矩阵

5.2 线性代数实现

标量

2. 向量

3. 矩阵

5.3 按特定轴求和

6 矩阵计算

6.1 导数的概念及几何意义

标量导数

亚导数 （偏导数）

一、\(\rm{function}\) 为是一个标量

二、\(\rm{function}\) 为是一个向量

三、\(\rm{function}\) 为是一个矩阵

6.3 矩阵求导的布局

7 自动求导

7.1 向量链式法则

链式法则示例

7.2 自动求导

一、计算图

二、自动求导的两种模式

7.3 代码部分

7.3 Q&A

亚导数（偏导数）