Econometrics

1 Introduction

本文为参考洪永淼老师《高级计量学》复习高级计量经济学的学习笔记。

2 一般回归分析和模型设定

2.1 条件概率分别

• 边际概率密度函数 （$\rm{P}_{18}$）

  $$\begin{align*} f_x(x) = \int_{-\infty}^\infty f_{XY}(x,y)\rm{d}y \end{align*}$$

• 给定 $X = x$，$Y$ 的条件概率密度函数 （$\rm{P}_{18}$）

  $$\begin{align*} f_{Y|X}(y|x) = \frac{f_{XY}(x,y)}{f_X{(x)}} \end{align*}$$

• 条件均值（$\rm{P}_{19}$）

  $$\begin{align*} E(Y|x) \equiv E(Y|X=x) = \int_{-\infty}^{\infty} y f_{Y|X}(y|x)\rm{d}y \end{align*}$$

• 条件方差（$\rm{P}_{19}$）

  $$\begin{align*} var(Y|x) \equiv var(Y|X=x) &= \int_{-\infty}^{\infty} [y-E(Y|x)]^2f_{Y|X}(y|x)\rm{d}y \\ &= E(Y^2|x)-[E(Y|x)]^2 \end{align*}$$

• 条件偏度（Conditional skewness）（$\rm{P}_{19}$）

  $$\begin{align*} S(Y|x) \equiv \frac{E[(Y-E(Y|x)]^3|x)}{[var(Y|x)]^{3/2}} \end{align*}$$

• 条件峰度（Conditional kurtosis）（$\rm{P}_{19}$）

  $$\begin{align*} K(Y|x) \equiv \frac{E[(Y-E(Y|x)]^4|x)}{[var(Y|x)]^{2}} \end{align*}$$

• 条件 $\alpha$ - 分位数（Conditional $\alpha$-quantile）（$\rm{P}_{19}$）

  $$\begin{align*} P[Y \leq Q(X, \alpha)|X = x] = \alpha \in (0,1) \end{align*}$$

2.2 条件均值与回归分析

2.2.1 定义

• 定义 2.1（$\rm{P}_{20}$）< 回归函数 (Regression Function) >：条件均值 $E(Y|X)$ 称为 $Y$ 对 $X$ 的回归函数;

2.2.2 定理

• 定理 2.1（$\rm{P}_{21}$）：$E(E(Y|X)) = E(Y)$；

• 定理 2.2（$\rm{P}_{21}$） < 重复期望法则 (Law of Interated Expectations, LIE) >：对给定的可测函数 $G(X,Y)$，假设期望 $E[G(X,Y)]$ 存在，则：

  $$\begin{align*} E[G(X, Y)] = E\{E[G(X,Y)|X])\} \end{align*}$$

• 定理 2.3（$\rm{P}_{23}$）< $MSE$ 最优解 >：条件均值 $E(Y|X)$ 是下列问题的最优解：

  $$\begin{align*} E(Y|X = \arg \min_{g\ \in\ \mathbb{F}} E[Y - g(X)]^2 \end{align*}$$

  其中，$\mathbb{F}$ 是所有可测和平方可积函数的集合 (Space of all measurable and quare-integrable functions)，即：

  $$\begin{align*} \mathbb{F} = \left\{g:\mathbb{R}^{k+1} \to \mathbb{R}\ \left| \int g^2(x) f_X(x) \rm{d}x < \infty \right.\right\} \end{align*}$$

  < 注：可通过中间变量 $g_0(X) \equiv E(Y|X)$ 证明 >

• 定理 2.4（$\rm{P}_{25}$）< 回归等式 (Regression Identity) >：给定条件均值 $E(Y|X)$，总有：

  $$\begin{align*} Y = E(Y|X) + \varepsilon \end{align*}$$

  其中，$\varepsilon$ 称为回归扰动项（Regression disturbance），满足：

  $$\begin{align*} E(\varepsilon|X) = 0 \end{align*}$$

2.3 线性回归建模

2.3.1 定义

• 定义 2.3（$\rm{P}_{29}$）< 仿射函数 (Affine Function) >：记 $X = (1, X_1, \dots , X_k)^\prime$，$\beta = (\beta_0, \beta_1, \dots, \beta_k)^\prime$。则仿射函数族定义为：

  $$\begin{align*} \mathbb{A} &= \left\{ g:\mathbb{R}^{k+1} \to \mathbb{R}\ |\ g(X) = \beta_0 + \sum_{j=1}^{k} \beta_jX_j, \beta_j \in \mathbb{R} \right\} \\ &= \left\{ g:\mathbb{R}^{k+1} \to \mathbb{R}\ |\ g(X) = X^\prime\beta \right\} \end{align*}$$

  这里，对参数向量 $\beta$ 的值没有限制。对于这族函数，函数形式一致，分别是解释变量和参数 $\beta$ 的线性函数；

• 定义 2.4（$\rm{P}_{32}$）< 线性回归模型 (Linear Regression Model) >：方程：

  $$\begin{align*} Y = X^\prime \beta + u, \beta \in \mathbb{R}^{k+1} \end{align*}$$

  称为 $Y$ 对 $X$ 的线性回归模型，其中 $u$ 是回归模型误差 (Regression model error)。如果 $k=1$，称为二元线性回归模型 (Bivariate linear regression model) 或直线回归模型 (Straight linere gression model)。如果 $k>1$，则称为多元线性回归模型 (Multiple linear regression model)；

2.3.2 定理

• 定理 2.5（$\rm{P}_{30}$）< 最优线性最小二乘预测 (Best Linear Least Squares Predictstion) > ：假设$E(Y^2) < \infty$，且$(k+1) \times (k+1)$ 矩阵 $E(X^\prime X)$ 是非奇异的。则以下优化问题：

  $$\begin{align*} \min_{g\ \in\ \mathbb{A} }E[Y - g(X)]^2 = \min_{\beta\ \in \mathbb{R}^{k+1}}E(Y - X^\prime \beta)^2 \end{align*}$$

  的解，即最优线性最小二乘法预测值为：

  $$\begin{align*} g^*(X) = X^\prime\beta^* \end{align*}$$

  其中最优系数向量为（$\star \star \star$）：

  $$\begin{align*} \beta^* = [E(X X^\prime)]^{-1}E(XY) \end{align*}$$

• 定理 2.6（$\rm{P}_{32}$）：假设定理 2.5 的条件成立。令：

  $$\begin{align*} Y = X^\prime \beta + u \end{align*}$$

  并令 $\beta^* = [E(XX^\prime)]^{-1}E(XY)$ 为最优线性最小二乘近似系数。则：

  $$\begin{align*} \beta = \beta^* \end{align*}$$

  当且仅当以下正交条件成立：

  $$\begin{align*} E(Xu) = 0 \end{align*}$$

2.4 条件均值的模型设定

2.4.1 定义

• 定义 2.5（$\rm{P}_{34}$）< 条件均值模型的正确设定 >：线性回归模型： $$\begin{align*} Y = X^\prime \beta + u, \beta \in \mathbb{R^{k+1}} \end{align*}$$ 是条件均值 $E(Y|X)$ 的正确设定，如果存在某个参数值 $\beta^o \in \mathbb{R^{k+1}}$，有： $$\begin{align*} E(Y|X) = X^\prime \beta^o \end{align*}$$ 另一方面，如果对于任意的参数值 $\beta \in \mathbb{R^{k+1}}$， $$\begin{align*} E(Y|X) \neq X^\prime \beta \end{align*}$$ 则称线性回归模型是对 $E(Y|X)$ 的错误设定 (Misspecified)；

2.4.2 定理

• 定理 2.7（$\rm{P}_{35}$）：如果线性回归模型：

  $$\begin{align*} Y = X^\prime \beta + u \end{align*}$$

  是对条件均值$E(Y|X)$ 的正确设定则：

  1）存在一个参数 $\beta^o$ 和一个随机变量 $\varepsilon$，有 $Y = X^\prime \beta^o+\varepsilon$，其中 $E(\varepsilon|X) = 0$；

  2）$\beta^* = \beta^o$

3. 经典线性回归模型

3.1 假设

• 假设 3.1（$\rm{P}_{45}$）< 线性 (Linearity) >：$\{Y_t, X_t^\prime\}_{t=1}^n$ 是一个可观测的随机样本，且：

  $$Y_t = X_t^\prime \beta^o + \varepsilon_t, t = 1, \dots, n$$

  其中，$\beta^o$ 是一个 $K \times 1 (K = k + 1)$ 未知参数向量，$\varepsilon_t$ 是一个不可观测的随机扰动项；

  令：

  $$\begin{align*} Y & = (Y_1, \dots , Y_n)^\prime, &n \times 1 \\ \varepsilon & = (\varepsilon_1, \dots , \varepsilon_n)^\prime, &n \times 1 \\ X & = (X_1, \dots , X_n)^\prime, &n \times K \\ \end{align*}$$

  这里 $X$ 的第 $t$ 行是 $K$ 维行向量 $X_t^\prime = (1, X_{1t},\dots,X_{kt})$。从而，(1) 式可以表示为：

  $$\begin{align*} Y = X \beta^o + \varepsilon \end{align*}$$

• 假设 3.2（$\rm{P}_{46}$）< 严格外生性 (Strict Exogeneity) >：

  $$\begin{align*} E(\varepsilon_t|X) = E(\varepsilon_t|X_1, \dots, X_t,\dots,X_n) = 0 \qquad t = 1,\dots,n \end{align*}$$

  这一假设隐含着 $E(Y_t|X_t)$ 的模型设定正确；

• 假设 3.3（$\rm{P}_{48}$）< 非奇异性 (Nonsingularity) >：

  1）$K \times K$ 方阵 $X^\prime X = \sum_\limits{t=1}^n X_t X_t^\prime$ 是非奇异的（排除了 $X_t$ 中存在多重共线性）；

  2）当 $n \to \infty$ 时，$X^\prime X$ 的最小特征值:

  $$\begin{align*} \lambda_{min}(X^\prime X) \to \infty \end{align*}$$

  的概率为 1;

• 假设 3.4（$\rm{P}_{49}$）< 球形误差方差 (Spherical Error Variance) >：

  1）条件同方差:

  $$\begin{align*} E(\varepsilon_t^2|X) = \sigma^2 > 0, \quad t =1,\dots,n \end{align*}$$

  2）条件不相关：

  $$\begin{align*} E(\varepsilon_t\varepsilon_s|X) = 0, t \neq s, \quad t,s \in \{1,\dots,n\} \end{align*}$$

  上述可写为：

  $$\begin{align*} E(\varepsilon_t\varepsilon_s|X) = \sigma^2 \delta_{ts} = \sigma^2I, \quad t,s \in \{1,\dots,n\} \end{align*}$$

  其中，$\delta_{ts} = 1$ 当且仅当 $t=s$；

3.1.1 总结

给定假设 3.2 和 3.4 意味着 $\varepsilon_t$ 存在条件同方差，即：

$$\begin{align*} var(\varepsilon_t|X) = E(\varepsilon_t^2|X) - [E(\varepsilon_t|X)]^2 = E(\varepsilon_t^2|X) = \sigma^2 \end{align*}$$

同样的，对于所有的 $t \neq s$，有：

$$\begin{align*} cov(\varepsilon_t,\varepsilon_s|X) = E(\varepsilon_t\varepsilon_s|X) = 0 \end{align*}$$

如果 $t$ 表示个体单元，这意味着 横截面不相关，如果 $t$ 表示时间，这意味着 序列不相关，为方便起见，这两种情况均称为 $\{\varepsilon_t\}$ 不存在自相关；

3.2 普通最小二乘法 (OLS)

3.2.1 定义

• 定义 3.1（$\rm{P}_{50}$）< $OLS$ 估计量 >：定义线性回归模型 $Y_t = X_t^\prime \beta + u_t$ 的残差平方和 (Sum of squared residuals, SSR) 为：

  $$\begin{align*} SSR(\beta) \equiv (Y - X\beta)^\prime(Y - X\beta) = \sum_{t=1}^{n}(Y_t - X_t^\prime\beta)^2 \end{align*}$$

  则普通最小二乘法 ( $OLS$ ) 估计量 $\hat\beta$ 是以下优化问题的解：

  $$\begin{align*} \hat \beta = \arg \min_{\beta\ \in \mathbb{R}^K} SSR(\beta) \end{align*}$$

  注： $OLS$ 具有以下良好性质（陈强，$\rm{P}_{87}$）：

  1）线性性。$OLS$ 估计量 $\hat \beta$ 为线性估计量（Linear estimator）。从 $OLS$ 估计量的表达式 $\hat \beta = (X^\prime X)^{-1} X^\prime Y$ 可知，$\hat \beta$ 可以视为 $Y$ 的线性组合，同时也是 $\varepsilon$ 的线性组合（将 $(X^\prime X)^{-1} X^\prime$ 视为系数矩阵，$\star\star\star$）。故为线性估计量。

  2）无偏性。$E(\hat\beta|X) = \beta$，即 $\hat\beta$ 不会系统地高估或低估 $\beta$，即定理 3.5 (1)。

  3）估计量 $\hat\beta$ 的协方差矩阵。$var(\hat \beta |X) = \sigma^2(X^\prime X)^{-1}$，见定理 3.5 (2)。

  4）最小方差性。所有无偏估计量中最小二乘估计的方差最小。

3.2.2 定理

• 定理 3.1（$\rm{P}_{50}$）< $OLS$ 的存在性 >：在假设 3.1 和 3.3 (1) 下， $OLS$ 估计量 $\hat \beta$ 存在，并且：

  $$\begin{align*} \hat \beta &= (X^\prime X)^{-1} X^\prime Y \\ & = \left(\frac{1}{n} \sum_{t = 1}^{n} X_t X_t^\prime\right)^{-1} \frac{1}{n} \sum_{t=1}^{n} X_t Y_t \end{align*}$$

  其中第二个表达式在后面章节的渐近分析中将经常用到。

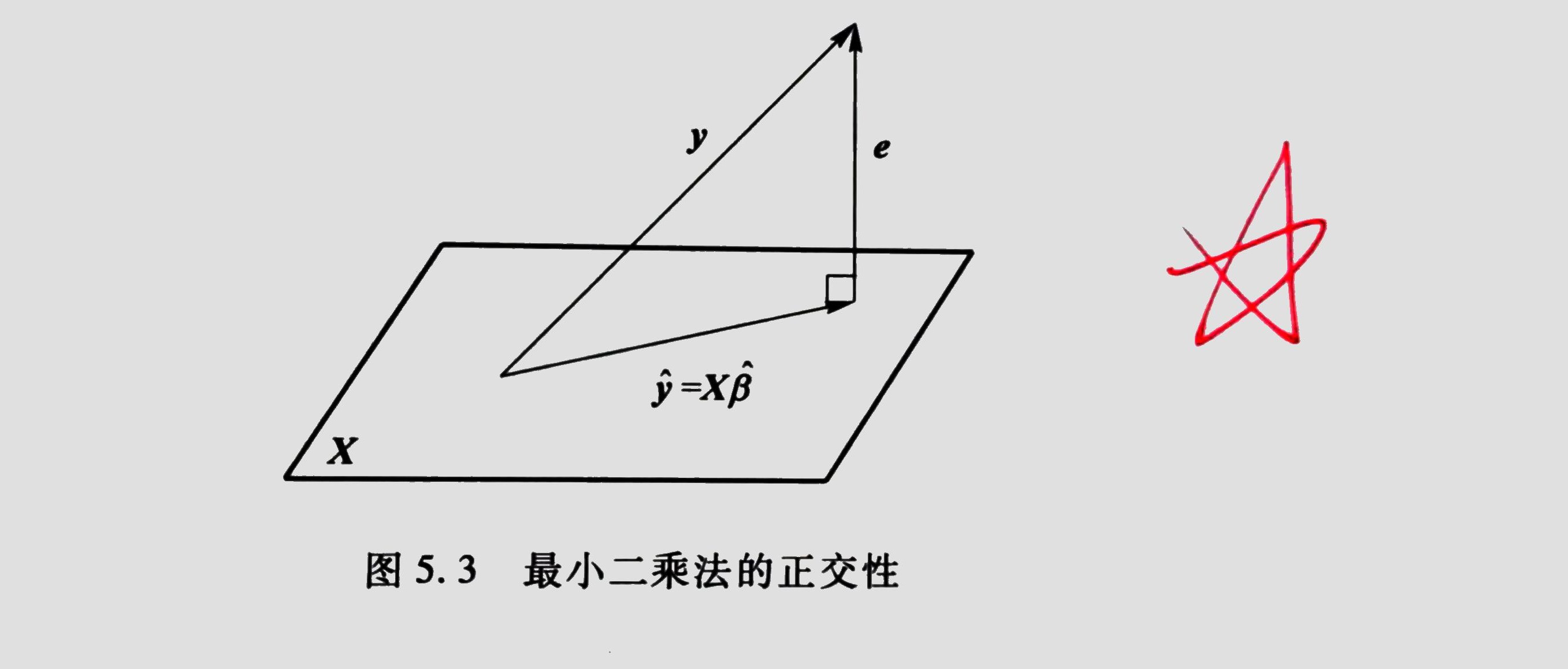
  注： $\hat Y_t \equiv X_t^\prime \hat\beta$ 称为观测值 $Y_t$ 的 拟合值或者预测值，而 $e_t \equiv Y_t - \hat Y_t$ 是观测值 $Y_t$ 的 估计残差或预测误差。被解释变量 $Y_t$ 可以分解为相互正交的拟合值 $\hat Y$ 与残差 $e$ 之和，参见 Fig. 3-1。

  

Fig. 3-1 OLS 的正交性

• 定理 3.2（$\rm{P}_{52}$）：给定假设 3.1 和 3.3 (1)，有：

  (1)

  $$\begin{align*} X ^\prime e = 0 \end{align*}$$

  (2)

  $$\begin{align*} \hat \beta - \beta^o = (X^\prime X)^{-1}X^{\prime}\varepsilon \end{align*}$$

  注： 上式可变为 $C\varepsilon$，其中 $C$ 是权重向量，因此，给定 $X, \hat\beta-\beta^o$ 是 $\varepsilon$ 的线性组合，当 $\varepsilon$ 服从联合正态分布时，$\hat\beta-\beta^o$ 也服从正态分布。

  (3) 定义 $n \times n$ 投影矩阵

  $$\begin{align*} P = X(X^\prime X)^{-1}X^{\prime} \end{align*}$$

  和

  $$\begin{align*} M = I_n - P \end{align*}$$

  则 $P$ 和 $M$ 是对称的（即 $P = P^{\prime}, M = M^{\prime}$）幂等矩阵（即 $P = P^{2}, M = M^{2}$），并且

  $$\begin{align*} PX = X \\ MX = 0 \end{align*}$$

  (4)

  $$\begin{align*} SSR(\hat \beta) = e^\prime e = Y^{-1} MY = \varepsilon^{\prime} M \varepsilon \end{align*}$$

  注：$e = Y - X \hat\beta = M \varepsilon$（$\star\star\star$）

3.3 拟合优度和模型选择准则

3.3.1 定义

• 定义 3.2（$\rm{P}_{54}$）< 非中心化 $\mathcal{R}^2$ >：非中心化多元相关系数平方 $\mathcal{R}^2$ 定义为：

  $$\begin{align*} \mathcal{R}^2_{uc} = \frac{\hat Y{}^\prime \hat Y}{Y^\prime Y} = 1 - \frac{e^\prime e}{Y^\prime Y} \end{align*}$$

  $\mathcal{R}^2$ 的含义是因变量 ${Y_t}$ 的非中心化的样本二次型变动可以被预测值 $\{\hat Y{}^\prime\}$ 的非中心化样本二次型变动所预测的比例。由定义可知，总有 $0 \leq \mathcal{R}^2_{uc} \leq 1$。

• 定义 3.3（$\rm{P}_{54}$）< 中心化 $\mathcal{R}^2$ 或决定系数 (Coefficient of Determination) >：决定系数定义为：

  $$\begin{align*} \mathcal{R}^2 &\equiv 1 - \frac{\sum_\limits{t=1}^{n} e_t^2}{\sum_\limits{t=1}^{n} (Y_t - \overline Y)^2} \\ &= 1 - \frac{SSE}{SST} = \frac{SSR}{SST} = \frac{\sum\limits_{i=1}^{n}(\hat{Y_i} - \bar Y)^2}{\sum\limits_{i=1}^{n}(Y_i - \bar Y)^2} \end{align*}$$

  其中 $\overline Y = n^{-1}\sum_\limits{t=1}^{n}Y_t$ 是样本均值。

  注：

  • 当 $X_t$ 包括截距项，即 $X_{0t} = 1$ 时，可进行如下正交分解：

    $$\begin{align*} \sum_{t=1}^{n}(Y_t - \overline Y)^2 &= \sum_{t=1}^{n}(\hat Y_t - \overline Y + Y_t - \hat Y_t)^2 \\ & = \sum_{t=1}^{n}(\hat Y_t - \overline Y)^2 + \sum_{t=1}^{n}e_t^2 \end{align*}$$

    此时（$\star \star\star$）：

    $$\begin{align*} \mathcal{R}^2 &\equiv 1 - \frac{e^\prime e}{\sum_\limits{t=1}^{n}(Y_t - \overline Y)^2}\\ &= \frac{\sum_\limits{t=1}^{n}(\hat Y_t - \overline Y)^2}{\sum_\limits{t=1}^{n}(Y_t - \overline Y)^2} \end{align*}$$

  • 如果 $X_t$ 不包括截距项，此时 $(X^\prime X)$ 是奇异矩阵，且可能有 $E(e_t) \neq 0$，所以有：

    $$\begin{align*} \sum_{t=1}^{n}(Y_t - \overline Y)^2 &= \sum_{t=1}^{n}(\hat Y_t - \overline Y)^2 + \sum_{t=1}^{n}e_t^2 + 2 \sum_{t=1}^{n}(\hat Y_t - \overline Y)e_t \\ &\neq \sum_{t=1}^{n}(\hat Y_t - \overline Y)^2 + \sum_{t=1}^{n}e_t^2 \end{align*}$$

    在这种情况下，$\mathcal{R}^2$ 可能为负值，因为交叉项 $\sum_\limits{t=1}^{n}(\hat Y_t - \overline Y)e_t$ 可能为负值。

3.3.2 定理

• 定理 3.3（$\rm{P}_{56}$）：$\mathcal{R}^2 = \hat \rho_{Y\hat Y}^2 = \frac{cov(Y, \hat Y)}{var(Y)var(\hat Y)}$，这里 $\hat \rho_{Y\hat Y}^2$ 是 $\{Y_t\}$ 和 $\{\hat Y_t\}$ 的样本相关系数。

• 定理 3.4（$\rm{P}_{56}$）：假设 $\{Y_t, X_{1t}, \dots, X_{
  (k+q)t}\}_{t=1}^n$ 是一容量为 $n$ 的随机样本，$\mathcal{R}_1^2$ 是下列线性回归模型的中心化拟合度：

  $$\begin{align*} Y_t= X_t^{\prime}\beta + \varepsilon_t \end{align*}$$

  其中， $X_t = (1, X_{1t}, \dots, X_{kt})^\prime$，$\beta$ 是 $K \times 1$ 未知参数向量；$\mathcal{R}_2^2$ 是下面扩展的线性回归模型的中心化扰合优度：

  $$\begin{align*} Y_t = \tilde X_t^\prime \gamma + u_t \end{align*}$$

  其中，$\tilde X_t = (1, X_{1t}, \dots, X_{kt}, X_{(k+1)t)})^\prime$，$\gamma$ 是 $(K+q) \times 1$ 未知参数向量，$q$ 是正整数。则：

  $$\begin{align*} \mathcal{R}_2^2 \geq \mathcal{R}_1^2 \end{align*}$$

  注：定理 3.4 有重要含义：

  • $\mathcal{R}^2$ 可用于 解释变量数目相等 的线性回归模型的比较，但它不适用于 比较不同解释变量数目 的线性模型，因为 模型的解释变量越多，$\mathcal{R}^2$ 就会越大。

  • $\mathcal{R}^2$ 也不是正确模型设定的判断标准。$\mathcal{R}^2$ 高并不意味着模型设定正确，事实上，给定解释变量 $X_t$，$\mathcal{R}_2$ 值的大小 与线性回归模型的信噪比 有关。

3.3.3 模型选择准则

1. Akaike 信息准则（Akaike information criterion, AIC）

   线性回归模型可通过选择合适的解释变量数模 $K$，以最小化下面的 Akaike 信息准则来选择模型。

   $$\begin{align*} AIC = {\rm{ln}}(s^2) + \frac{2K}{n} \end{align*}$$

   其中，

   $$\begin{align*} s^2 = e^\prime e / (n - K) \end{align*}$$

   $K = k+1$ 是自变量 $X_t$ 的数目，第一项 ${\rm{ln}} s^2$ 测度模型的拟合优度，而第二项 $2K/n$ 测度模型的复杂程度。另外，$s^2$ 是 $E(\varepsilon_t^2) = \sigma^2$ 的残差方差估计量（Residual variance estimator）。

2. Bayesian 信息准则（Bayesian information criterion, BIC）

   线性模型也可以通过选择合适的 $K$，以最小化以下 $Bayesian$ 信息准则来选择模型：

   $$\begin{align*} BIC = {\rm{ln}} (s^2) +\frac{K {\rm{ln}}(n)}{n} \end{align*}$$

3. $\overline{\mathcal{R}}{}^2$

   我们知道 $\mathcal{R}^2$ 的定义为：

   $$\begin{align*} \mathcal{R}^2 = 1 - \frac{e^\prime e / n}{\sum_\limits{t=1}^{n}(Y_t - \overline Y)^2 / n} = 1 - \frac{SSE}{SST} \end{align*}$$

   其中，$e^\prime e / n$ 和 $\sum_\limits{t=1}^{n}(Y_t - \overline Y)^2 / n$ 分别是方差 $\sigma^2 = var(\varepsilon_t)$ 和 $\sigma_Y^2 = var(Y_t)$ 的有偏估计。残差平方和：$SSE$（书中为 $SSR$（residual），调整的 $\mathcal{R}^2$ 为：

   $$\begin{align*} \overline{\mathcal{R}}{}^2 = 1 - \frac{e^\prime e / (n-K)}{(n-1)^{-1}\sum_\limits{t=1}^{n}(Y_t - \overline Y)^2} = 1 - \frac{n-1}{n-K}(1 - \mathcal{R}) \end{align*}$$

   此时有：$E[e^\prime e / (n-K)] = \sigma^2$ 和 $E[(n-1)^{-1}\sum_\limits{t=1}^{n}(Y_t - \overline Y)^2] = \sigma_Y^2$ ，在 $\overline{\mathcal{R}}{}^2$ 中，调整的是自由度，此时即使 $X_t$ 中包含截距项，$\bar{\mathcal{R}}$ 也可能取负值。

   $\bar{\mathcal{R}}$ 作用：① 消除解释变量的多少对决定系数计算的影响。② 可用于比较解释变量个数不同的模型，而 $\mathcal{R}$ 则不能比较。

3.4 $OLS$ 估计量的无偏性和有效性

3.4.1 定理

• 定理 3.5（$\rm{P}_{60}$）：如果假设 3.1、3.3 (1) 和 3.4 成立，则：

  1）无偏性 < Unbiasedness > ：$E(\hat \beta|X) = \beta^o$，并且 $E(\hat\beta) = \beta^o$；
  注：将 $(X^\prime X)^{-1} X^\prime$ 视为系数矩阵（$\star\star\star$）。

  2）方差偏小性 < Vanishing variance > 所有无偏估计中，最小二乘的方差最小：

  $$\begin{align*} var(\hat \beta |X) = E\{[\hat\beta - E(\hat \beta|X)][\hat\beta - E(\hat\beta|X)]^\prime |X\} = \sigma^2(X^\prime X)^{-1} \end{align*}$$

  如果假设 3.3 (2) 也成立，那么对于任意的 $K \times 1$ 向量 $\tau$，满足 $\tau^\prime \tau = 1$，有：

  $$\begin{align*} \mathsf{当} n \to \infty \mathsf{时，}\tau^\prime var(\hat\beta|X)\tau \to 0 \end{align*}$$

  3）正交性 < Orthogonality between $e$ and $\beta$ > ：

  $$\begin{align*} cov(\hat \beta, e|X) = 0 \end{align*}$$

  4）Gauss - Markov 定理：对于任意的线性无偏估计量 $\hat b, var(\hat b|X) - var(\hat\beta|X)$ 是半正定 (Positive semi-definite, PSD) 的（说明 $\hat{\beta}$ 是方差最小的。

  5）残差方差估计量 < Residual variance estimator >：

  $$\begin{align*} s^2 = e^\prime e/(n - K) = \frac{1}{n - K }\sum_\limits{t = 1}^{n} e_t^2 \end{align*}$$

  是 $\sigma^2 = E(\varepsilon_t^2)$ 的无偏估计量，即 $E(s^2 | X) = \sigma^2$。

  注： 由于随机变量 $\{e_t\}$ 必须满足 $K$ 个正规方程 $X^\prime e = 0$，故其中只有 $(n - K)$ 个残差是（自由）独立的，经过自由度校正后，才是无偏估计。如果样本容量 $n$ 很大，当 $n \to \infty$ 时，$\frac{n - K}{n} \to 1$，是否进行“小样本校正”并无多大区别。

3.5 $OLS$ 估计量的抽样分布

3.5.1 假设

• 假设 3.5（$\rm{P}_{65}$）< 条件正态分布 (Conditional Normality) >：$\varepsilon|X \sim N(0, \sigma^2 I)$ 。

  假设 3.5 可以推出假设 3.2（$E(\varepsilon|X) = 0$） 和假设 3.4 （$E(\varepsilon_t\varepsilon_s|X) = \sigma^2I$）。事实上，在假设 3.5 下，$\varepsilon$ 的条件概率密度函数：

  $$\begin{align*} f(\varepsilon|X) = \frac{1}{(\sqrt{2 \pi \sigma^2})^n}exp(-\frac{\varepsilon^\prime \varepsilon} {2\sigma^2}) = f(\varepsilon) \end{align*}$$

  不依赖于 $X$，从而随机扰动项 $\varepsilon$ 独立于 $X$。因此， $\varepsilon$ 的任何条件矩均不依赖于 $X$。

3.5.2 定理

• 定理 3.6（$\rm{P}_{65}$）< $\hat\beta$ 的条件正态分布 >：给定假设 3.1、3.3 (1) 和 3.5，对所有的 $n>K$：

  $$\begin{align*} (\hat \beta - \beta^o)|X \sim N[0, \sigma^2(X^\prime X)^{-1}] \end{align*}$$

• 推论 3.7（$\rm{P}_{66}$）< $R(\hat\beta - \beta^o)$ 的条件正态分布 >：给定假设 3.1、3.3 (1) 和 3.5，则对于任何非随机的 $J \times K$ 矩阵 $R$（$J$ 为参数限制数目），有：

  $$\begin{align*} R(\hat \beta - \beta^o)|X \sim N[0, R \sigma^2(X^\prime X)^{-1} R^\prime] \end{align*}$$

  其中，$R$ 可以视为一个选择矩阵，如 $R = (1, 0, 0, \cdots, 0)$，则 $R(\hat{\beta} - \beta^o) = \hat{\beta}_0 - \beta_0^o$，在假设检验中需要用到 $R(\hat{\beta} - \beta^o_0)$ 的抽样分布。但由于 $var(\varepsilon_t) = \sigma^2$ 是未知的，因此要估计 $\sigma^2$。

3.6 $OLS$ 估计量的方差 - 协方差矩阵的估计

3.6.1 定理

• 引理 3.8（$\rm{P}_{66}$）< 正态随机变量的二次型 (Quadratic Form of Normal Random Variables) >：如果一个 $m\times 1$ 随机变量 $v \sim N(0, 1)$，并且 $Q$ 是一个 $m \times m$ 非随机对称幂等矩阵， 秩 $1\leq m$，则二次型：

  $$\begin{align*} v^\prime Q v \sim \chi^2_q \end{align*}$$

  在以下引用中，$v = \varepsilon/\sigma\sim N(0,1), Q = M$。因为 $rank(M) = n - K$，所以：

  $$\begin{align*} \left.\frac{e^\prime e}{\sigma^2} \right|X \sim \chi^2_{n-K} \end{align*}$$

• 引理 3.9（$\rm{P}_{67}$）< 残差方差的估计量 (Residual Variance Estimator) >：给定假设 3.1、3.3 (1) 和 3.5，则对于任意的 $n\leq K$，有：

  1）

  $$\begin{align*} \left.\frac{(n-K)s^2}{\sigma^2} \right|X = \left.\frac{e^\prime e}{\sigma^2} \right|X \sim \chi^2_{n-K} \end{align*}$$

  其中，$e = M\varepsilon$。
  2）给定 $X$ 的条件下，$s^2$ 和 $\hat\beta$ 是独立的。从定理 3.4(3) 可知：$cov(\hat{\beta, e|X}) = 0$，对于联合正态分布而言，零相关意味着相互独立。

3.7 参数假设检验

3.7.1 定义

• 定义 3.4（$\rm{P}_{73}$）< 依分布收敛 (Convergence in Distribution) > ：假设 $\{Z_n, n= 1, 2, \dots\}$ 是一个分布函数为$\{F_n(z) = P(Z_n \leq z)\}$ 的随机变量或随机向量的序列，$Z$ 是一个不依赖于 $n$ 的分布函数为 $F(z) = P(Z \leq z)$ 的随机变量或随机向量。称 $Z_n$ 依分布收敛于 $Z$，如果在分布函数 $F(z)$ 的任何连续点，$Z_n$ 的分布函数值均收敛于 $Z$ 的分布函数值，即： $$\begin{align*} \lim_{n\to\infty} F_n(z) = F(z) \end{align*}$$ 或等价地： $$\begin{align*} \mathsf{当}\ n\to\infty\ \mathsf{时}, F_n(z) \to F(z) \end{align*}$$ 用符号 $Z_n \overset{d}{\to} Z$ 表示。$Z$ 的分布称为 $Z_n$ 的渐近分布或极限分布。

3.7.2 定理

• 推论 3.10（$\rm{P}_{71}$）：给定假设 3.1、3.3 (1) 和 3.5，当原假设 $\mathbb{H}_0: R\beta^o = r$ 成立时，对于每一个 $n\geq K$，有：

$$\begin{align*} (R\hat\beta - r)|X \sim N[0, \sigma^2 R(X^\prime X)^{-1}R^\prime] \end{align*}$$

• 推论 3.11（$\rm{P}_{76}$）：如果 $q \times 1$ 随机向量 $Z \sim N(0, V)$，其中 $V = var(Z)$ 是一个 $q\times q$ 对称、非奇异的方差 - 协方差矩阵，则：

  $$\begin{align*} Z^\prime V^{-1}Z \sim \chi_q^2 \end{align*}$$

• 定理 3.12（$\rm{P}_{78}$）：给定假设 3.1、3.3 (1) 和 3.5，当原假设 $\mathbb{H}_0: R\beta^o = r$ 成立时，对于每一个 $n\geq K$，有：

  $$\begin{align*} F = \frac{(R \hat\beta - r)^\prime[R(X^\prime X)^{-1}R^\prime]^{-1}(R \hat\beta - r)/J}{s^2} \sim F_{J,n-K} \end{align*} \\ \frac{s^2(n-K)}{\sigma^2} \sim \chi^2(n-K)$$

• 定理 3.13（$\rm{P}_{79}$）：给定假设 3.1、3.3 (1) ，令 $SSR_u = e^\prime e$ 是以下无约束回归模型的残差平方和：

  $$\begin{align*} Y = X\beta^o + \varepsilon \end{align*}$$

  令 $SSR_r = \tilde e^\prime \tilde e$ 是以下有约束模型的残差平方和 ：

  $$\begin{align*} Y = X\beta^o + \varepsilon \end{align*}$$

  其约束条件为：

  $$\begin{align*} R \beta^o = r \end{align*}$$

  这里 $\tilde e = Y - X \tilde \beta$，$\tilde \beta$ 是有约束回归模型的 $OLS$ 估计量。则 $F$ 检验统计量可写为：

  $$\begin{align*} F = \frac{(\tilde e^\prime \tilde e - e^\prime e)/J}{e^\prime e/(n - K)} \end{align*}$$

• 定理 3.14（$\rm{P}_{81}$）：给定假设 3.1、3.3 (1) 和 3.5，则当原假设是 $\mathbb{H}_0: R\beta^o = r$ 成立且 $n \to \infty$ 时，$Wald$ 检验统计量：

  $$\begin{align*} \mathcal{W} = \frac{(R\hat\beta - r)^\prime[R(X^\prime X)^{-1} R^\prime]^{-1}(R\hat\beta - r)}{s^2} = J \cdot F \overset{d}{\to}\chi^2_J \end{align*}$$

  可以发现，这里定义的 $Wald$ 检验统计量与 $F$ 检验统计量 只相差一个比例常数 $J$，这是因为目前考虑条件同方差的情形。如果存在条件异方差，仍然可以定义 $Wald$ 检验统计量，但是 $W = J \cdot F$ 这一关系将不再成立。

3.9 广义最小二乘估计

经典线性回归模型依赖于关键假设—假设 3.5（$\varepsilon|X \sim N(0, \sigma^2 I)$ ）。除了条件正态分布外，还隐含不存在条件异方差和自相关性。

3.9.1 假设

• 假设 3.6（$\rm{P}_{87}$）：$\varepsilon|X \sim N(0, \sigma^2 V)$，其中 $0 < \sigma^2 < \infty$ 是未知的，但 $V = V(X)$ 是一个已知的对称与有限的 $n \times n$ 正定矩阵。

  从假设可知条件方差（$\star\star\star$）：

  $$\begin{align*} var(\varepsilon|X) = E(\varepsilon^\prime\varepsilon|X) = \sigma^2V = \sigma^2 V(X) \end{align*}$$

  虽然 $var(\varepsilon|X)$ 仅包含一个未知常数 $\sigma^2$，但它允许存在已知形式的条件异方差 $V(X)$。

3.9.2 定义

3.9.3 定理

• 定理 3.15（$\rm{P}_{87}$）：给定假设 3.1、3.3 (1) 和 3.6，则：

  1）无偏性：$E(\hat\beta|X) = \beta^o$；

  2）方差：$var(\hat\beta|X) = \sigma^2(X^\prime X)^{-1} X^\prime VX(X^\prime X)^{-1} \neq \sigma^2(X^\prime X)^{-1}$；

  3）正态分布：$(\hat\beta - \beta^o)|X \sim N[0,\sigma^2 (X^\prime X)^{-1}X^\prime VX(X^\prime X)^{-1}]$；

  4）相关性：$cov(\hat\beta,e|X) = E[(X^\prime X)^{-1} X^\prime \varepsilon \varepsilon^\prime M] = \sigma^2 (X^\prime X)^{-1} X^\prime V M \neq 0$（其中，$V \neq I, e = M \varepsilon, M = I - P, P = X(X^\prime X)^{-1} X$）。

  相关性表明，由于给定 $X, \hat \beta$ 和 $e$ 存在相关性，$t$ 检验和 $F$ 检验统计量定义中的分子和分母不再独立，所以不能得到有限样本条件下的 $t$ 分布和 $F$ 分布。为了解决该问题，需要考虑新的估计方法——GLS。

• 引理 3.16（$\rm{P}_{88}$）：对于任意的 $n \times n$ 对称正定矩阵 $V$，总可以写成：

  $$\begin{align*} V^{-1} &= C^\prime C \\ V &= C^{-1}(C^\prime)^{-1} \end{align*}$$

  这里，$C$ 是一个 $n \times n$ 非奇异矩阵。这称为 Cholesky 分解（Cholesky factorization），其中 C 可能是非对称矩阵。

  考虑线性回归模型：

  $$\begin{align*} CY = (CX)\beta^o + C \varepsilon \end{align*}$$

  令 $Y^ = CY, X^ = CX, \varepsilon^* = C\varepsilon$。所以有：

  $E(\varepsilon^*|X) = E(C \varepsilon|X) = 0$;

  $var(\varepsilon^*|X) = CE(\varepsilon \varepsilon^\prime | X) C^\prime = \sigma^2 CVC^\prime = \sigma^2 I$ ;

  变换后的回归模型的 $OLS$ 估计量为：

  $$\begin{align*} \hat\beta{}^* = (X^{*\prime}X^*)^{-1}(X^{*\prime}Y^*) = (X^\prime V^{-1}X)^{-1} X^\prime V^{-1} Y \end{align*}$$

  称为广义最小二乘 ($GLS$) 估计量。变换后的 $\hat{\beta^}$ 和 $e^$ 不相关，故 $t$ 和 $F$ 检验可用：

  $$\begin{align*} T^* &= \frac{R \hat\beta {}^* - r}{\sqrt{s^*{}^2 {R(X{}^*}^\prime {X{}^*})^{-1}R^\prime}} \sim t(n-K) \\ F{}^* &= \frac{(R \hat\beta {}^* - r)^\prime[{R(X{}^*}^\prime {X{}^*})^{-1}R^\prime]^{-1}(R \hat\beta{}^* - r)}{s^2} \sim F_{J,n-K} \end{align*}$$

• 定理 3.17（$\rm{P}_{91}$）：给定假设 3.1、3.3 (1) 和 3.6，则：

  1）无偏性：$E(\hat\beta{}^*|X) = \beta^o$；

  2）方差：$var(\hat\beta{}^|X) = \sigma^2(X^{\prime} X^*)^{-1} = \sigma^2(X^\prime V^{-1} X)^{-1}$；

  3）相关性：$cov(\hat\beta{}^,e^|X) = 0$，其中 $e^ = Y^ - X^ \hat\beta{}^$；

  4）$\hat\beta{}^*$ 是最优线性无偏估计量(BLUE);

  5）$(s^{2}|X) = \sigma^2$，其中 $s^{2} = e^{\prime}e^/(n-K)$。

4 独立同分布随机样本的线性回归模型

在 $var(\varepsilon | X) = \sigma^2 V$ 形式未定时，仍可用 $OLS$ 估计量 $\hat \beta$，根据正确的方差公式 $var(\hat\beta|X) = \sigma^2(X^\prime X)^{-1} X^\prime VX(X^\prime X)^{-1}$，可构造 $var(\hat\beta|X)$ 的估计量，此时经典的 $t$ 和 $F$ 检验已不再适用，因为他们建立在不正确的 $var(\hat\beta|X)$ 上的，此时，仅能适用渐近分布理论。

4.1 渐近理论导论

4.1.1 定义

• 定义 4.1（$\rm{P}_{103}$）< 依均方收敛或依二次方均值收敛 (Convergence in Mean Squares or in Quadratic Mean) > ：一个随机变量（或固定维数的随机向量，即 $Z_n$ 的维数不随 $n$ 的增加而变化）序列 $\{Z_n, n = 1, 2, \dots\}$ 依均方收敛于随机变量（或随机向量） $Z$，如果当 $n \to \infty$ 时，有：

  $$\begin{align*} E\ \Vert Z_n - Z \Vert^2 \to 0 \end{align*}$$

  其中，$\Vert \cdot \Vert$ 是随机变量或随机向量的模。记 $Z_n \overset{q.m.}{\to} Z$。

  注：当 $Z_n$ 是一个固定维数的随机向量时，可理解为 $Z_n$ 的每一个元素的序列收敛于 $Z$ 的相对应元素。如果 $Z_n - Z$ 是一个 $l \times m$ 的矩阵时，可将平方模定义为：

  $$\begin{align*} \Vert Z_n - Z \Vert^2 = \sum_{t=1}^{l}\sum_{s = 1}^{m} [Z_n - Z]^2_{(t, s)} \end{align*}$$

• 定义 4.2（$\rm{P}_{103}$）< 依概率收敛 (Convergence in Probability) > ：一个随机变量序列 $\{Z_n, n = 1, 2, \dots\}$ 依概率收敛于 $Z$，如果对任意给定的常数 $\epsilon > 0$，有：

  $$\begin{align*} \mathsf{当}\ n\to \infty \mathsf{时},\ Pr[\ \Vert Z_n - Z \Vert >\epsilon] \to 0 \end{align*}$$

  或等价地：

  $$\begin{align*} \mathsf{当}\ n\to \infty \mathsf{时},\ Pr[\ \Vert Z_n - Z \Vert \leq \epsilon] \to 1 \end{align*}$$

  对于依概率收敛，可记为 $Z_n - Z \overset{p}{\to} 0$ 或 $Z_n - Z = O_P(1)$。

• 定义 4.3（$\rm{P}_{106}$）< 依概率有界 (Boundedness in Probability) > ：一个随机变量序列 $\{Z_n, n = 1, 2, \dots\}$ 依概率有界的，如果对任意小的常数 $\delta > 0$，存在常数 $C= C(\delta)< \infty$，使得，当 $n \to \infty$ 时，有：

  $$\begin{align*} P(\ \Vert Z_n \Vert > C\ ) \leq \delta \end{align*}$$

  记为 $Z_n = O_P(1)$。

• 定义 4.4（$\rm{P}_{108}$）< 几乎必然收敛 (Almost sure convergence)) > ：$\{Z_n, n = 1, 2, \dots\}$ 几乎必然收敛于 $Z$，如果：

  $$\begin{align*} \Pr[\lim_{n\to\infty}\Vert Z_n - Z \Vert = 0] = 1 \end{align*}$$

  记为 $Z_n - Z \overset{a.s.}{\to}$ 或 $Z_n - Z = o_{a.s.}(1)$。

  注：几乎必然收敛可以推出依概率收敛，但依概率收敛不一定能推出几乎必然收敛。

4.1.2 定理

• 引理 4.1（$\rm{P}_{105}$）< 独立同分布样本的弱大数定律 (Weak Law of Large Numbers (WLLN) for I.I.D Samples) > ：假设随机样本 $\{Z_t\}^n_{t=1}$ 服从 $i.i.d.(\mu,\sigma^2)$，并定义 $\bar Z_n = n^{-1} \sum_\limits{t=1}^{n} Z_t$，这里 $n = 1,2,\cdots$。则当 $n \to \infty$ 时：

  $$\begin{align*} \bar Z_n \overset{p}{\to} \mu \end{align*}$$

• 引理 4.2（$\rm{P}_{105}$）< 独立同分布随机样本的弱大数定律 (WLLN for I.I.D Samples) > ：假设 $\{Z_t\}^n_{t=1}$ 是一个独立同分布随机样本，$E(Z_t) = \mu$ 且 $E |Z_t| < \infty$。定义 $\bar Z_n = n^{-1} \sum_\limits{t=1}^{n} Z_t$，则当 $n \to \infty$ 时：

  $$\begin{align*} \bar Z_n \overset{p}{\to} \mu \end{align*}$$

• 引理 4.3（$\rm{P}_{106}$）：如果 $Z_t - Z \overset{q.m.}{\to} 0$，则 $Z_t - Z \overset{p}{\to} 0$。

• 引理 4.4（$\rm{P}_{109}$）< 独立同分布随机样本的强大数定律 (Strong Law of Large Numbers (SLLN) for I.I.D Samples) > ：假设 $\{Z_t\}^n_{t=1}$ 是一个独立同分布随机样本，$E(Z_t) = \mu$ 且 $E |Z_t| < \infty$。则当 $n \to \infty$ 时：

  $$\begin{align*} \bar Z_n \overset{a.s.}{\to} \mu \end{align*}$$

• 引理 4.5（$\rm{P}_{109}$）< 连续性 (Continuity) > ：

  1）假设当 $n \to \infty$ 时，$A_n - A \overset{p}{\to} 0, B_n - B \overset{p}{\to} 0$，且 $g(\cdot)$ 和 $h(\cdot)$ 是连续函数。则：

  $$\begin{align*} [g(A_n) + h(B_n)] - [g(A) + h(B)] \overset{p}{\to} 0 \\ g(A_n)h(B_n) - g(A)h(B) \overset{p}{\to} 0 \end{align*}$$

  2）对于几乎必然收敛，也有类似结论。

• 引理 4.6（$\rm{P}_{110}$）< 独立同分布随机样本的中心极限定理 (CLT for I.I.D Random Samples) >：假设 $\{Z_t\}_{t=1}^{n}$ 是一个 $i.i.d.(\mu, \sigma^2)$ 随机样本呢，这里 $Z_t$ 是随机变量。定义 $\bar Z_n = n^{-1} \sum_\limits{t=1}^n Z_t$ 时，有：

  $$\begin{align*} \frac{\bar Z_n - E(\bar Z_n)}{\sqrt{var(\bar Z_n)}} = \frac{\sqrt{n}(\bar Z_n - \mu)}{\sigma} \overset{d}{\to} N(0,1) \end{align*}$$

• 引理 4.7（$\rm{P}_{112}$）< Cramer-Wold 方法 > ：假设 $Z_n$ 和 $Z$ 均是 $p \times 1$ 随机向量，这里 $p$ 是一个固定正整数。令 $n \to \infty$。则 $Z_n \overset{d}{\to} Z$，当且仅当对于任意非零的 $\tau \in R^p$，且满足 $\tau^\prime\tau = 1$，使得：

  $$\begin{align*} \tau^\prime Z_n \overset{d}{\to} \tau^\prime Z \end{align*}$$

• 定理 4.8（$\rm{P}_{112}$）< Slutsky 定理 > ：令 $Z_n \overset{d}{\to}Z, a_n \overset{d}{\to} a$ 且 $b_n \overset{d}{\to}b$, 其中 $a$ 和 $b$ 是常数。则当 $n \to \infty$ 时，有 ：

  $$\begin{align*} a_n + b_n Z_n \overset{d}{\to} a + bZ \end{align*}$$

• 定理 4.9（$\rm{P}_{112}$）< Delta 方法 > ：假设 $\sqrt n(Z_n - \mu)/\sigma \overset{d}{\to} N(0,1)$，$g(\cdot)$ 是连续可导的函数。且 $g^\prime(\mu) \neq 0$。则当 $n \to \infty$ 时，有 $\sqrt n [g(\bar Z_n) - g(\mu)] = g^\prime(\mu)\sqrt n(\bar Z_n - \mu) + O_P(1)$，且：

  $$\begin{align*} \sqrt n [g(\bar Z_n) - g(\mu)] &\overset{d}{\to} N\{0,\sigma^2[g^\prime(\mu)]^2\} \\ g(\bar{Z}_n) &= g(\mu) + g^\prime(\bar{\mu}_n)(\bar{Z}_n - \mu) \\ \bar{\mu}_n &= \lambda \mu + (1 - \lambda) \bar{Z}_n, \lambda \in [0, 1] \end{align*}$$

4.2 线性回归模型假设

4.2.1 假设

• 假设 4.1（$\rm{P}_{114}$）< 独立同分布 (I.I.D) > ：$\{Y_t,X_t^\prime\}$ 是一个可观测的独立同分布随机样本（独立同分布意味着，对于 $t \neq s, cov(\varepsilon_t, \varepsilon_s) = 0$，回归扰动项不存在自相关）；

• 假设 4.2（$\rm{P}_{114}$）< 线性 (Linearity) > ：

  $$\begin{align*} Y_t = X_t^\prime \beta^o + \varepsilon_t \qquad t = 1,\cdots,n \end{align*}$$

• 假设 4.3（$\rm{P}_{114}$）< 正确模型设定 (Correct Model Specification) > ：$E(\varepsilon_t|X_t) = 0$ 且 $E(\varepsilon_t^2) = \sigma^2 < \infty$；

• 假设 4.4（$\rm{P}_{114}$）< 非奇异性同分布 (Nonsingularity) > ： $K\times K$ 阶矩阵 $Q = E(X_t X_t^\prime)$ 是对称、有限与非奇异的；

  由强大数定理可知：$n \to \infty$ 时，$\frac{X^\prime X}{n} = \frac 1 n \sum\limits_{t=1}^{n}X_t X_t^\prime \overset{a.s}{\to} E(X_t X_t^\prime) = Q$

• 假设 4.5（$\rm{P}_{114}$）： $K\times K$ 阶矩阵 $V \equiv var(X_t \varepsilon_t) = E(X_t X_t^\prime\varepsilon_t^2)$ 是对称、有限与正定 (PD) 的；

这些假设的一个重要特征时：不要求 $\varepsilon$ 服从条件正态分布，同时允许条件异方差，即 $var(\varepsilon|X_t) \neq \sigma^2$。

4.3 $OLS$ 估计量的一致性

由假设 4.4 可知，对于所有的 $j\in\{0, 1, \cdots, k\}, E(X_{jt}^2)<\infty$。根据对立同分布随机样本的强大数据定律（引理 4.4），当 $n \to \infty$ 时，有：

$$\begin{align*} \frac{X^\prime X}{n} = \frac{1}{n}\sum_{t=1}^{n} X_t X_t^\prime \overset{a.s.}{\to}E(X_t X_t^\prime) = Q \qquad (\star\star\star) \end{align*}$$

假设有一个随机样本 $\{Y_t, X_t^\prime\}_{t=1}^n$。回忆 $OLS$ 估计量：

$$\begin{align*} \hat \beta = (X^\prime X)^{-1}X^\prime Y = \hat Q{}^{-1} n^{-1} \sum_{t=1}^{n} X_t Y_t \end{align*}$$

其中，

$$\begin{align*} \hat Q{}^{-1} = n^{-1} \sum_{t=1}^{n} X_t X_t^\prime \end{align*}$$

将 $Y_t = X_t^\prime \beta^o + \varepsilon_t$（参见假设 4.2）代入，得：

$$\begin{align*} \hat \beta = \beta^o + \hat Q{}^{-1} n^{-1}\sum_{t=1}^{n} X_t \varepsilon_t \end{align*}$$

$\hat{\beta} - \beta^o = \hat{Q}{}^{-1}\sum\limits_{t=1}^{n} X_t \varepsilon_t \overset{P}{\to} 0$ 下面考察 $\hat\beta$ 的一致性。

4.3.1 定理

• 定理 4.10（$\rm{P}_{116}$）< $OLS$ 估计量的一致性 (Consistency of OLS) > ：给定假设 4.1-4.4，且当 $n\to\infty$ 时，有： $$\begin{align*} \hat\beta \overset{d}{\to} \beta^o \mathsf{或} \hat\beta - \beta^o = O_P(1) \end{align*}$$

4.4 $OLS$ 估计量的渐近正态性

4.4.1 假设

• 假设 4.6（$\rm{P}_{119}$）< 条件同方差 (Conditional Homoskedasticity) >：$E(\varepsilon_t^2|X_t) = \sigma^2$。

4.4.2 定理

• 引理 4.11（$\rm{P}_{117}$）< 独立同分布随机样本的多元中心极限定理 (Multivariate CLT for I.I.D. Random Samples) >：假设 $\{Z_t\}^n_{t=1}$ 是一个独立同分布随机样本，且 $E(Z_t) = 0, var(Z_t) = E(Z_t Z_t^\prime) = V$ 是一个有限、对称与正定的矩阵，定义：

  $$\begin{align*} \bar Z_n = n^{-1} \sum_{t=1}^n Z_t \end{align*}$$

  则当 $n \to \infty$ 时，有：

  $$\begin{align*} \sqrt n \bar Z_n \overset{d}{\to} N(0, V) \end{align*}$$

  或等价地：

  $$\begin{align*} V^{-\frac{1}{2}} \sqrt n \bar Z_n \overset{d}{\to} N(0, I) \end{align*}$$

  其中，$I$ 是一个维数与 $V$ 相同的单位矩阵。引理 4.11 表明，$V \equiv var(Z_t)$ 是 $\sqrt n \bar Z_n$ 的渐近分布的方差，简称 $\sqrt n \bar Z_n$ 的渐近方差，记为 $avar(\sqrt n \bar Z_n) = V$。

• 定理 4.12（$\rm{P}_{118}$）< $OLS$ 估计量的渐近正态分布 (Asymptotic Normality of OLS) >：给定假设 4.1-4.5，则当 $n\to \infty$ 时，有：

  $$\begin{align*} \sqrt n (\hat \beta - \beta^o) \overset{d}{\to} N(0, Q^{-1}VQ^{-1}) \end{align*}$$

  其中 $V \equiv var(X_t\varepsilon_t) = E(X_t X_t^\prime \varepsilon_t^2)$。

• 定理 4.13（$\rm{P}_{119}$）：给定假设 4.1-4.6，则当 $n\to \infty$ 时，有：

  $$\begin{align*} \sqrt n (\hat \beta - \beta^o) \overset{d}{\to} N(0, \sigma^2Q^{-1}) \end{align*}$$

  定理 4.13 表明，当存在条件同方差时，$\sqrt n(\bar \beta - \beta^o)$ 的渐近方差 ($\star\star\star$) 为：

  $$\begin{align*} avar(\sqrt n \hat \beta) = \sigma^2Q^{-1} \end{align*}$$

4.5 渐近方差估计量

4.5.1 定理

1. 条件同法差

在这种情况下，由定理 4.13，$\sqrt{n}(\hat\beta - \beta^o)$ 渐近方差为：

$$\begin{align*} avar(\sqrt n \hat \beta) = \sigma^2 Q^{-1} \end{align*}$$

• 引理 4.14（$\rm{P}_{120}$）：给定假设 4.1、4.2 和 4.4，则：

  $$\begin{align*} \hat Q = n^{-1} \sum_{t=1}^n X_t X_t^\prime \overset{p}{\to} Q \end{align*}$$

  其次，考虑估计 $\sigma^2$。因为 $\sigma^2 = E(\varepsilon_t^2)$，可使用样本残差方差估计量：

  $$\begin{align*} s^2 = e^\prime e/(n-K) = \frac{1}{n-K} \sum_{t=1}{n} e_t^2 \end{align*}$$

• 定理 4.15（$\rm{P}_{120}$）：< $\sigma^2$ 的一致估计量 (Consistent Estimator of $\sigma^2$)>：给定假设 4.1-4.4，当 $n \to \infty$ 时，有：

  $$\begin{align*} s^2 \overset{p}{\to} \sigma^2 \end{align*}$$

• 定理 4.16（$\rm{P}_{121}$）：< 条件同方差下 $\sqrt n (\hat\beta - \beta^o)$ 的渐近方差估计量 (Asymototic Variance Estimator of OLS Under Conditional Homoskedasticity) >：给定假设 4.1-4.4，当 $n \to \infty$ 时，有：

  $$\begin{align*} s^2 \hat Q {}^{-1} \overset{p}{\to} avar(\sqrt n \hat \beta) = \sigma^2 Q^{-1} \end{align*}$$

  $\sqrt n (\hat\beta - \beta^o)$ 的渐近方差估计量是：

  $$\begin{align*} s^2 \hat Q {}^{-1} = s^2(X^\prime X /n)^{-1} \end{align*}$$

  这等价于，当 $n$ 很大时，$(\hat\beta - \beta^o)$ 的方差估计量近似为：

  $$\begin{align*} s^2 \hat Q {}^{-1}/n = s^2(X^\prime X)^{-1} \end{align*}$$

2. 条件异方差

在存在条件异方差（即 $E(\varepsilon_t^2|X_t) \neq \sigma^2$) 时，$\sqrt n (\hat\beta - \beta^o)$ 的渐近方差为：

$$\begin{align*} avar(\sqrt n \hat \beta) = Q^{-1} V Q^{-1} \end{align*}$$

其中，$V = E(X_t X_t^\prime \varepsilon_t^2)$。

• 引理 4.17（$\rm{P}_{122}$）：给定假设 4.1-4.5 和 4.7，则当 $n \to \infty$ 时，有

  $$\begin{align*} \hat V = \frac{1}{n} \sum_{t = 1}^{n} X_t X_t^\prime e_t^2 \overset{p}{\to} V \end{align*}$$

• 引理 4.18（$\rm{P}_{123}$）< 条件异方差下 $\sqrt n \hat \beta$ 的渐近方差估计量 (Asymptotic Variance Estimator of OLS Under Conditional Heteroskedasticity) >：给定假设 4.1-4.5 和 4.7，则当 $n \to \infty$ 时，有

  $$\begin{align*} \hat Q{}^{-1} \hat V \hat Q{}^{-1} \overset{p}{\to} avar{\sqrt n \hat \beta} = Q^{-1} V Q^{-1} \end{align*}$$

  这就是 $\sqrt n \hat \beta$ 的 $White (1980)$ 异方差一致性方差 - 协方差矩阵估计量 (Heteroskedasticity-consistent variance-covariance matrix estimator)。因此，当存在条件异方差及 $n$ 很大时，$\hat \beta - \beta^o$ 的方差估计量为:

  $$\begin{align*} \frac{\hat Q{}^{-1} \hat V \hat Q{}^{-1}}{n} &= \frac{(X^\prime X /n)^{-1} \hat V (X^\prime X /n)^{-1}}{n}\\ &= (X^\prime X)^{-1} X^\prime D(e) D(e)^\prime X (X^\prime X)^{-1}\\ &\neq s^2(X^\prime X)^{-1} \end{align*}$$

  其中 $D(e) = diag(e_1, \cdots, e_n) \neq s^2 I$。

4.5.2 假设

• 假设 4.7（$\rm{P}_{122}$）：(1) 对于所有的 $j \in \{0,1,\cdots,k\}, E(X_{jt}^4)<\infty$。(2) $E(X\varepsilon_{t}^4)<\infty$。

  $$\begin{align*} s^2 \hat Q {}^{-1} \overset{p}{\to} avar(\sqrt n \hat \beta) = \sigma^2 Q^{-1} \end{align*}$$

  注：渐近方差估计 $\hat Q {}^{-1} V \hat Q {}^{-1}$ 在条件同方差下也是渐近有效的，即 $\hat Q {}^{-1} V \hat{Q}{}^{-1} \overset{P}{\to} Avar(\sqrt{n}\hat{\beta}) = \sigma^2 Q{}^{-1}$，但在有限样本条件下，可能不如 $\sigma^2 Q^{-1}$ 表现好，因为后者利用了条件同方差这一信息。

4.6 参数假设检验

下面考虑如何构建统计量以检验原假设：

$$\begin{align*} \mathbb{H}: R\beta^o = r \end{align*}$$

其中 $R$ 时 $J \times K$ 满秩矩阵，$r$ 是 $J \times 1$ 常向量，且 $J \leq K$。

首先考虑统计量 $R \hat\beta - r = R(\hat\beta - \beta^o) + R\beta^o - r$，所以再原假设 $\mathbb{H}: R\beta^o = r$ 下有：

$$\begin{align*} \sqrt n (R \hat\beta - r) &= R\sqrt n(\hat\beta - \beta^o) \\ &\overset{d}{\to} N(0, RQ^{-1}VQ^{-1}R^\prime) \end{align*}$$

其中，$\hat Q = \frac{X^{\prime} X}{n} \overset{P}{\to} Q, s^2 \overset{P}{\to} \sigma^2$。

1. 条件同方差情形($V = \sigma^2 Q$)

• 定理 4.19（$\rm{P}_{125}$）< $t$ 检验 >：给定假设 4.1-4.4 和 4.6，则当假设 $\mathbb{H}_0: R\beta^o = r$ 成立， $J = 1$，且 $n\to \infty$ 时，经典 $t$ 检验统计量：

  $$\begin{align*} T &= \frac{\sqrt n(R\beta_o - r)}{\sqrt{\sigma^2 R Q^{-1} R^{\prime}}} \\ &= \frac{R\beta_o - r}{\sqrt{s^2 R (nQ)^{-1} R^{\prime}}} \\ &= \frac{R\beta^o - r}{\sqrt{s^2 R(X^\prime X)^{-1}R^\prime}} \overset{p}{\to} N(0, 1) \end{align*}$$

• 定理 4.20（$\rm{P}_{125}$）< 渐近 $\chi^2$ 检验 >：给定假设 4.1-4.4 和 4.6，则当假设 $\mathbb{H}_0: R\beta^o = r$ 成立， $J \leq 1$，且 $n\to \infty$, $Wald$ 检验统计量（同方差，方差可知：

  $$\begin{align*} \mathcal{W} &\equiv (R\beta^o - r)^\prime[s^2 R(X^\prime X)^{-1}R]^{-1}(R\beta^o - r) \\ &= J \cdot F \overset{d}{\to} \chi^2_J \end{align*}$$

• 定理 4.21（$\rm{P}_{126}$）< $(n-K)\mathcal{R}^2$ 检验 >：给定假设 4.1-4.6，检验以下原假设：

  $$\begin{align*} \mathbb{H}_0:\beta^o_0 = \beta^o_1 = \cdots = \beta^o_k = 0 \end{align*}$$

  其中，$\beta^o_0, \beta^o_1, \cdots, \beta^o_k$ 是线性回归方程:

  $$\begin{align*} Y = \beta^o_0 + \beta^o_1 X_{1t} + \cdots + \beta^o_k X_{kt} + \varepsilon_t \end{align*}$$

  除截距项 $\beta_0^o$ 意外的所有回归系数。令 $\mathcal{R}^2$ 是无约束线性回归模型的决定系数，则当原假设 $\mathbb{H}_0$ 成立及 $n \to \infty$ 时，有：

  $$\begin{align*} (n - K) \mathcal{R}^2 \overset{d}{\to} \chi^2_k \end{align*}$$

  其中，$\mathcal{R}^2$ 的定义（$\rm{P}_{82}$）为：

  $$\begin{align*} \mathcal{R}^2 &= 1 - \frac{e^\prime e}{(Y - \bar Y l)^\prime (Y - \bar Y l)} = 1 - \frac{e^\prime e}{\tilde e{}^\prime \tilde e} \\ & \frac{R^2/(k-1)}{(1-R^2)/(n-K)} \overset{d}{\to} F(K-1, n-K) \end{align*}$$

  在原假设 $\mathcal{H}_0: \beta_1^o = \cdots = \beta_k^o = 0$ 时，$R^2 \overset{P}{\to} 0$。

2. 条件异方差情形($V \neq \sigma^2 Q$)
在原假设 $\mathbb{H}_0: R \beta^o = r$ 成立的条件下，有：

$$\begin{align*} \sqrt n (R \hat\beta - r) \overset{d}{\to} N(0, RQ^{-1}VQ^{-1}R^\prime) \end{align*}$$

其中，$V = E(X_t X_T^\prime \varepsilon_t^2)$，因此有

$$\begin{align*} \frac{R\beta^o - r}{\sqrt{R Q^{-1} V Q^{-1} R^\prime}} \overset{p}{\to} N(0, 1) \end{align*}$$

给定 $\hat Q \overset{p}{\to} Q, \hat V \overset{p}{\to} V$，这里 $\hat V = X^\prime D(e) D(e)^\prime X/n$，并由 Slutsky 定理，可定义稳健性 $t$ 检验统计量：

$$\begin{align*} T_r \equiv \frac{\sqrt n(R \hat\beta - r)}{\sqrt{R \hat Q{}^{-1} \hat V \hat Q{}^{-1} R^\prime}} \end{align*}$$

当 $\mathbb{H}_0:R\beta^o = r$ 成立，且 $n \to \infty$ 时，有：

$$\begin{align*} T_r \overset{p}{\to} N(0, 1) \end{align*}$$

这里，稳健性 (Robustness) 是指，当存在条件异方差时，$T_r$ 也是渐近有效的。

• 定理 4.22（$\rm{P}_{128}$）< 条件异方差下的稳健 $t$ 检验 (Robust t-Test Under Conditional Heteroskedasticity) >：给定假设 4.1-4.5 和 4.7，则当原假设 $\mathbb{H}_0: R \beta^o = r$ 成立。

  当 $J = 1$，且 $n \to \infty$ 时，稳健 $t$ 检验统计量为：

  $$\begin{align*} T_r \equiv \frac{\sqrt n(R \hat\beta - r)}{\sqrt{R \hat Q{}^{-1} \hat V \hat Q{}^{-1} R^\prime}} \overset{p}{\to} N(0, 1) \end{align*}$$

  当 $J \geq 1$，在原假设 $\mathbb{H}_0: R \beta^o = r$ 下，有二次型：

  $$\begin{align*} \mathcal{W} &\equiv \sqrt n (R\hat \beta - r)^\prime[R \hat Q{}^{-1} \hat V \hat Q{}^{-1} R^\prime]^{-1}\sqrt n(R\hat \beta - r) \\ &\overset{d}{\to} \chi^2_J \end{align*}$$

  其中，

  $$\begin{align*} \hat Q &= \frac{X^\prime X}{n}\\ \hat V &= var(X_t e_t) = \frac{X^\prime D(e)D(e)^\prime X}{n} \end{align*}$$

  这里，$D(e) = diag\{e_1, 2_2, \cdots,e_n\}$。

• 定理 4.23（$\rm{P}_{128}$）< 条件异方差下的稳健 $Wald$ 检验 (Robust Wald Test Under Conditional Heteroskedasticity) >：给定假设 4.1-4.5 和 4.7，则当原假设 $\mathbb{H}_0: R \beta^o = r$ 成立，且 $n \to \infty$ 时，有：

  $$\begin{align*} \mathcal{W} &\equiv \sqrt n (R\hat \beta - r)^\prime[R \hat Q{}^{-1} \hat V \hat Q{}^{-1} R^\prime]^{-1}\sqrt n(R\hat \beta - r) \\ &\overset{d}{\to} \chi^2_J \end{align*}$$

  异方差下，方差不可知，用渐近分布估计方差。

4.7 条件异方差检验

$White$ 条件异方差检验

考虑原假设：$\mathbb{H}_0: E(\varepsilon_t^2|X_t) = \sigma^2$，其中，$\varepsilon_t$ 是 $Y_t = X_t^\prime \beta^o + \varepsilon_t$ 的随机扰动项。

非零假设为：

$$\begin{align*} \varepsilon_t^2 &= \gamma^\prime \rm{vech}(X_t X_t^\prime) + v_t \\ &= \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_t X_1 X_2 + \beta_s X_1 X_3 + \cdots + v_t \end{align*}$$

其中，$\rm{vech}(X_t X_t^\prime)$ 是一个向量化算子，它将 $K \times K$ 对称矩阵 $X_t X_t^\prime$ 下三角元素转变为一个 $\frac{K(K+1)}{2} \times 1$ 向量。在 $\mathbb{H}_0: E(\varepsilon_t^2|X_t) = \sigma^2$ 下，$\varepsilon_t^2$ 与任何 $X_t$ 都不相关，故除截距项外，所有斜率系数均为零。

假设 $E(\varepsilon_t^4|X_t) = \mu_4$，可以得到：

$$\begin{align*} (n-J-1)\tilde{\mathcal{R}} \overset{d}{\to} \chi_J^2 \end{align*}$$

5 平稳时间序列的线性回归模型

5.1 时间序列分析导论

5.1 定义

• 定义 5.1（$\rm{P}_{137}$）< 随机时间序列过程 (Stochastic Time Series Process) >：一个随机时间序列过程 $\{Z_t\}$ 是由概率法则 $(\Omega, \mathbb{F}, P)$ 支配而产生的随机变量或向量序列。其中， $t \in \{\cdots, 0, 1, 2, \cdots\}$ 代表时间，$\Omega$ 是样本空间，$\mathbb{F}$ 是 $\sigma -$ 域，$P: \mathbb{F} \to [0, 1]$ 是概率测度。