0%

Scikit-learn

Posted on Edited on In , ,
Symbols count in article: 11k Reading time ≈ 10 mins.

1 Installing scikit-learn

  • Windows

    1
    pip install -U scikit-learn

  • macOS

    1
    pip install -U scikit-learn

  • Linux

    1
    pip3 install -U scikit-learn

Check installation:

1
pip show scikit-learn

See more about scikit-learn via clicking here.

2 General study mode

Steps:

  1. Load datas
  2. Split datas into two part: train and test part
  3. Training model
  4. Testing and evaluating model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# instance for iris
import numpy as np 
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

iris = datasets.load_iris()
iris_x = iris.data # features
iris_y = iris.target # types

# print(iris_X[:2, :])
x_train, x_test, y_train, y_test = train_test_split(iris_x, iris_y, test_size = 0.3) # split original data into train and test part
# the percentage of test sets is 30%

# print(y_train) # 会打乱原始数据
knn = KNeighborsClassifier() # Classifier
knn.fit(x_train, y_train) # Train
print(knn.predict(x_test)) # Use trained model to predict
print(y_test)

Result:

1
2
[1 1 0 0 0 2 2 0 0 2 1 0 2 0 0 2 2 2 0 1 2 1 0 1 0 1 2 2 1 0 2 0 1 1 0 0 0 0 1 2 1 2 0 2 2]
[1 1 0 0 0 2 2 0 0 2 1 0 2 0 0 2 2 2 0 1 2 1 0 1 0 1 2 2 1 0 2 0 1 1 0 0 0 0 1 2 1 2 0 2 2]

3 Sklearn.datasets

3.1 Generate regressiong datas

1
2
3
4
5
6
7
8
9
10
11
12
# instance for making datasets
from sklearn import datasets
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

X, y = datasets.make_regression(n_samples = 100, 
                n_features = 1, n_targets = 1, noise = 2)
# X, y = datasets.make_regression(n_samples = 100, 
#                 n_features = 1, n_targets = 1, noise = 10)

plt.scatter(X, y)
plt.show()

Result:

fig. 3-1 Synthetic data

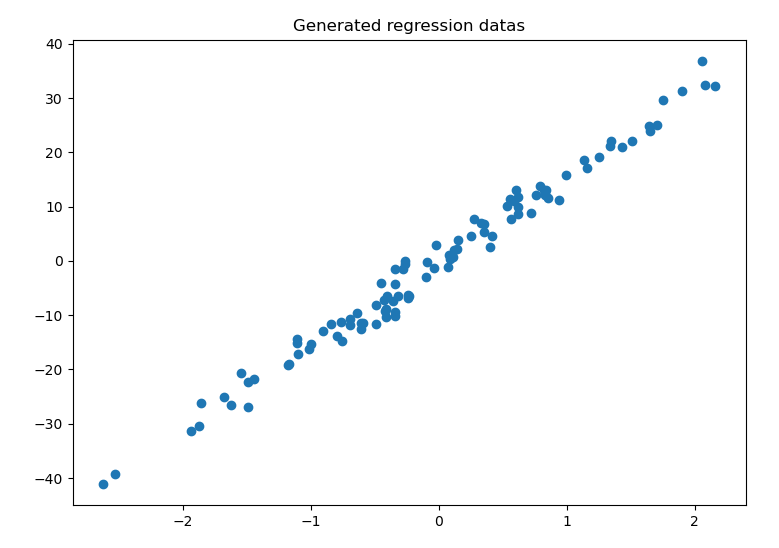
3.2 Load datasets of Linear Regression

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# instance for loading boston datasets
from sklearn import datasets
from sklearn.linear_model import LinearRegression

# LinearRegression example
loaded_data = datasets.load_boston()
# X, y = datasets_loadboston(retern_X_y = true)
data_X, data_y = loaded_data.data, loaded_data.target

model = LinearRegression()
model.fit(data_X, data_y)

print(data_y[:4])
print(model.predict(data_X[:4, :]))

Result:

1
2
[24.  21.6 34.7 33.4]
[30.00384338 25.02556238 30.56759672 28.60703649]

3.3 Normalization

  • Demo

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    from sklearn import preprocessing
    import numpy as np
    from sklearn.model_selection import train_test_split
    # cross_validation 更新为 model_selection
    from sklearn.datasets.samples_generator import make_classification
    from sklearn.svm import SVC
    import matplotlib.pyplot as plt

     a = np.array([[10, 2.7, 3.6],
                   [-100, 5, 2],
                   [120, 20, 40]], dtype = np.float64)

    print(a)
    print(preprocessing.scale(a)) # normalization

    Result:

    1
    2
    3
    4
    5
    6
    [[  10.     2.7    3.6]
     [-100.     5.     2. ]
     [ 120.    20.    40. ]]
    [[ 0.         -0.85170713 -0.66102858]
     [-1.22474487 -0.55187146 -0.75220493]
     [ 1.22474487  1.40357859  1.41323351]]

  • Comparison of accuracy before and after normalization

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    from sklearn import preprocessing
    import numpy as np
    from sklearn.model_selection import train_test_split
    # cross_validation 更新为 model_selection
    from sklearn.datasets.samples_generator import make_classification
    from sklearn.svm import SVC
    import matplotlib.pyplot as plt

    X, y = make_classification(n_samples = 300, n_features = 2, n_redundant = 0,n_informative = 2, random_state = 22, n_clusters_per_class = 1, scale = 100)
    # random_state: 固定随机数

    plt.scatter(X[:, 0], X[:, 1], c = y)
    plt.title('Classification samples')
    plt.show() #

    Plot the generated samples:

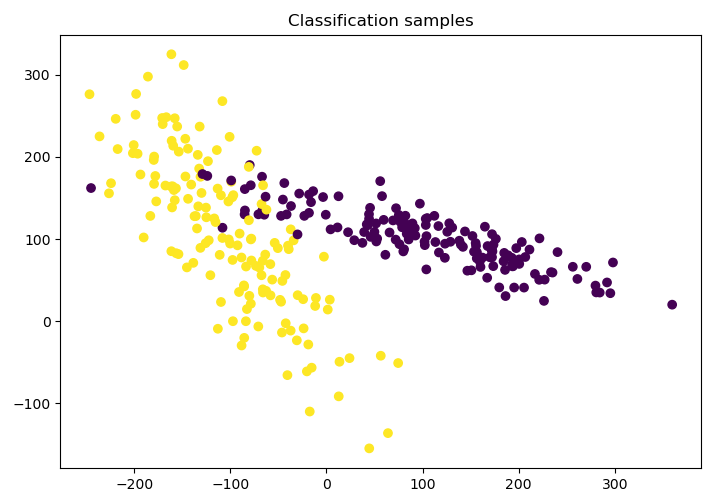
    fig. 3-2 Samples

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    X_train, X_test, y_train, y_test = train_test_split(X, y ,test_size = .3)
    clf = SVC()
    clf.fit(X_train, y_train)
    print(clf.score(X_test, y_test))

    X = preprocessing.scale(X) # normalization
    X_train, X_test, y_train, y_test = train_test_split(X, y ,test_size = .3)
    clf = SVC()
    clf.fit(X_train, y_train)
    print(clf.score(X_test, y_test))

    Result:

    1
    2
    0.9111111111111111
    0.9555555555555556

4 Model features and attributes

4.1 Basic parameters

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn import datasets
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# LinearRegression example
loaded_data = datasets.load_boston()
# X, y = datasets_loadboston(retern_X_y = true)
data_X, data_y = loaded_data.data, loaded_data.target

model = LinearRegression()
model.fit(data_X, data_y)

print(data_y[:4])
print(model.predict(data_X[:4, :]))

print(model.coef_) # 系数
print(model.intercept_) # 截距
print(model.get_params) # 参数
print(model.score(data_X, data_y)) # default is R^2 coefficietn of determination

Result:

1
2
3
4
5
6
7
8
9
[24.  21.6 34.7 33.4]
[30.00384338 25.02556238 30.56759672 28.60703649]
[-1.08011358e-01  4.64204584e-02  2.05586264e-02  2.68673382e+00
 -1.77666112e+01  3.80986521e+00  6.92224640e-04 -1.47556685e+00
  3.06049479e-01 -1.23345939e-02 -9.52747232e-01  9.31168327e-03
 -5.24758378e-01]
36.459488385089855
<bound method BaseEstimator.get_params of LinearRegression()>
0.7406426641094095

4.2 Cross validation

  • Evaluate the NN

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    from sklearn.datasets import load_iris
    from sklearn.model_selection import train_test_split
    from sklearn.neighbors import KNeighborsClassifier

    from sklearn.model_selection import cross_val_score

    iris = load_iris()
    X = iris.data
    y = iris.target

    X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 4)

    knn = KNeighborsClassifier(n_neighbors = 5)
    # knn.fit(X_train, y_train)
    # print(knn.score(X_test, y_test))
    scores = cross_val_score(knn, X, y, cv = 5, scoring = 'accuracy') # 将test进行5次划分
    print(scores.mean()) # 取平均值

    Result:

    1
    0.9733333333333334

  • Cross validation

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    from __future__ import print_function
    from sklearn.model_selection import  learning_curve
    from sklearn.datasets import load_digits
    from sklearn.svm import SVC
    import matplotlib.pyplot as plt
    import numpy as np

    digits = load_digits()
    X = digits.data
    y = digits.target
    train_sizes, train_loss, test_loss= learning_curve( SVC(gamma=0.01), X, y, cv=10, scoring='neg_mean_squared_error', train_sizes=[0.1, 0.25, 0.5, 0.75, 1])
    # 'neg_mean_squared_error' 非 'mean_squared_error'

    train_loss_mean = -np.mean(train_loss, axis=1)
    test_loss_mean = -np.mean(test_loss, axis=1)

    plt.plot(train_sizes, train_loss_mean, 'o-', color="r",
                 label="Training")
    plt.plot(train_sizes, test_loss_mean, 'o-', color="g",
                 label="Cross-validation")

    plt.xlabel("Training examples")
    plt.ylabel("Loss")
    plt.legend(loc="best")
    plt.show()

    Result:

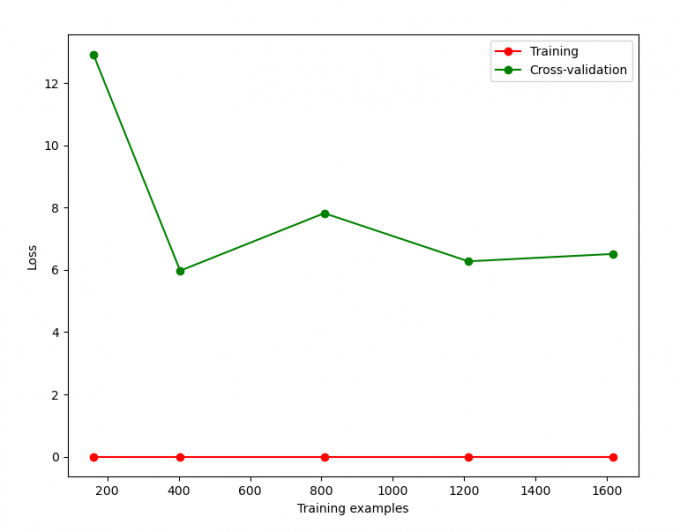
    fig 4-1 Vross-validation

  • Adjustment parameter-1

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    from __future__ import print_function
    from sklearn.datasets import load_iris
    from sklearn.model_selection import train_test_split
    from sklearn.neighbors import KNeighborsClassifier

    iris = load_iris()
    X = iris.data
    y = iris.target

    # test train split #
    X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=4)
    knn = KNeighborsClassifier(n_neighbors=5)
    knn.fit(X_train, y_train)
    y_pred = knn.predict(X_test)
    print(knn.score(X_test, y_test))

    # this is how to use cross_val_score to choose model and configs #
    from sklearn.model_selection import cross_val_score
    import matplotlib.pyplot as plt
    k_range = range(1, 31)
    k_scores = []
    for k in k_range:
        knn = KNeighborsClassifier(n_neighbors=k)
    ##    loss = -cross_val_score(knn, X, y, cv=10, scoring='mean_squared_error') # for regression
        scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy') # for classification
        k_scores.append(scores.mean())

    plt.plot(k_range, k_scores)
    plt.xlabel('Value of K for KNN')
    plt.ylabel('Cross-Validated Accuracy')
    plt.show()

    Result:

    fig. 4-2 Adjustment parameters

  • Adjustment parameter-2

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    from __future__ import print_function
    from sklearn.model_selection import validation_curve
    from sklearn.datasets import load_digits
    from sklearn.svm import SVC
    import matplotlib.pyplot as plt
    import numpy as np

    digits = load_digits()
    X = digits.data
    y = digits.target
    param_range = np.logspace(-6, -2.3, 5)
    train_loss, test_loss = validation_curve(
            SVC(), X, y, param_name='gamma', param_range=param_range, cv=10,
            scoring= 'neg_mean_squared_error')
    train_loss_mean = -np.mean(train_loss, axis=1)
    test_loss_mean = -np.mean(test_loss, axis=1)

    plt.plot(param_range, train_loss_mean, 'o-', color="r",
                 label="Training")
    plt.plot(param_range, test_loss_mean, 'o-', color="g",
                 label="Cross-validation")

    plt.xlabel("gamma")
    plt.ylabel("Loss")
    plt.title('Overfitting problem')
    plt.legend(loc="best")
    plt.show()

    Result:

    fig 4-3 Adjustment parameters

4.3 Transform target in regression model

将原始数据转化为分类模式，可以有效地提高预测的精度，效果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

# print(__doc__)

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeCV
from sklearn.compose import TransformedTargetRegressor
from sklearn.metrics import median_absolute_error, r2_score
from sklearn.utils.fixes import parse_version

if parse_version(matplotlib.__version__) >= parse_version('2.1'):
    desity_param = {'density': True}
else:
    density_param = {'normed': True}
    
X, y = make_regression(n_samples = 10000, noise = 100, random_state = 0)
y = np.exp((y + abs(y.min()))/200)
y_trans = np.log1p(y)

f, (ax0, ax1) = plt.subplots(1, 2)

# density: normalization
ax0.hist(y, bins = 100, density = True)
ax0.set_xlim([0, 2000])
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')

ax1.hist(y_trans, bins = 100, density = True)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')

f.suptitle('Synthetic data', y = 0.035)
f.tight_layout(rect = [0.05, 0.05, 0.95, 0.95])

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)

Result:

fig.4-4 Comparison of Transformation

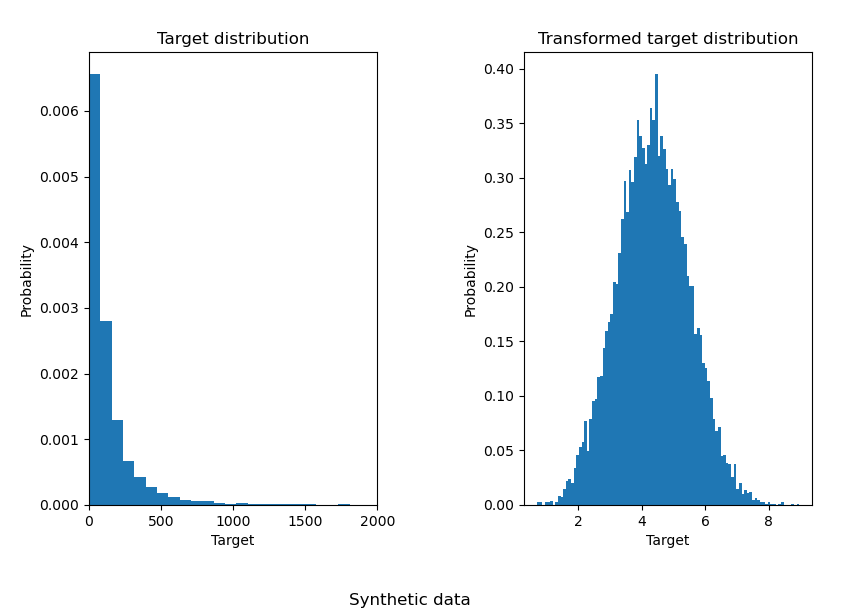
然后，再来测试其对预测精度的影响：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)

regr = RidgeCV()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)

ax0.scatter(y_test, y_pred)
ax0.plot([0, 2000], [0, 2000], '--k')
ax0.set_ylabel('Target predicted')
ax0.set_xlabel('True Target')
ax0.set_title('Ridge regression \n without target transformation')
ax0.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0.set_xlim([0, 2000])
ax0.set_ylim([0, 2000])

regr_trans = TransformedTargetRegressor(regressor=RidgeCV(), func=np.log1p,inverse_func=np.expm1)

regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)

ax1.scatter(y_test, y_pred)
ax1.plot([0, 2000], [0, 2000], '--k')
ax1.set_ylabel('Target predicted')
ax1.set_xlabel('True Target')
ax1.set_title('Ridge regression \n with target transformation')
ax1.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax1.set_xlim([0, 2000])
ax1.set_ylim([0, 2000])

f.suptitle("Synthetic data", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

fig. 4-5 Comparison before and after transforming

从结果可以看出，经过预处理转化后的数据集能有效地提高预测的精度，降低 MAE 的值。

5 Save model

Train model

1
2
3
4
5
6
7
8
from __future__ import print_function
from sklearn import svm
from sklearn import datasets

clf = svm.SVC()
iris = datasets.load_iris()
X, y = iris.data, iris.target
clf.fit(X, y)

Then, we can use two methods to save our trained models:

  1. pickle

    1
    2
    3
    4
    5
    6
    7
    8
    import pickle
    # Save
    with open('save/clf.pickle', 'wb') as f:
        pickle.dump(clf, f)
    # Restore
    with open('save/clf.pickle', 'rb') as f:
    	clf2 = pickle.load(f)
    print(clf2.predict(X[0:1]))

  2. joblib

    1
    2
    3
    4
    5
    6
    import joblib
    # Save
    joblib.dump(clf, './save/clf.pkl')
    # restore
    clf3 = joblib.load('save/clf.pkl')
    print(clf3.predict(X[0:1]))
-------------This blog is over! Thanks for your reading-------------